الدرس الرابع: الطرح مع إعادة التجميع
الكلمات المفتاحية 
إعادة التجميع
تمهيد
تعلمنا في الدرس السابق تقدير ناتج الطرح من خلال التقريب لأقرب 100 أو أقرب 1000.
أستكشف
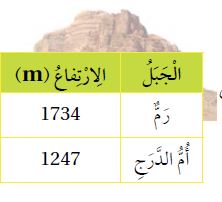
يُبَيِّنُ الْجَدْوَلُ الْمُجاوِرُ ارْتِفاعَ كُلٍّ مِنْ جَبَلِ وادي رَمٍّ وَجَبَلِ أُمِّ الدَّرَجِ. كَمِ الْفَرْقُ بَيْنَ ارْتِفاعَيِ الْجَبَلَيْنِ؟ 
نلاحظ أنه المطروح من منزلة الآحاد (7) وهو عدد أكبر من العدد في منزلة الآحاد في المطروح منه (4)لذا نحتاج إلى إعادة التجميع
سوف نتعلم في هذا الدرس طرح عددين مكونين من أربع منازل مع إعادة التجميع.
أتعلم
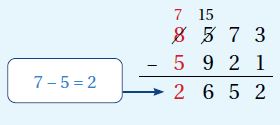
لِطَرْحِ الْعَدَدِ 5921 مِنْ 8573 أَطْرَحُ الْحادَ، فَالْعَشَراتِ، فَالْمِئاتِ، فَالُْلوفَ، وَقَدْ أَحْتاجُ إِلى إِعادَةِ التَّجْميعِ.
أُقَدِّرُ:
الخْطوْة 1: أَطْرَحُ الْآحادَ.
الخُْطوَْةُ 2: أَطْرَحُ الْعَشَراتِ
الخُْطوَْةُ 3: أَطْرَحُ الْمِئاتِ.
ألاحظ أنه لطرح 9 مئات من 5 مئات أعيد تجميع 1 من الألوف إلى 10 مئات وأضيفها إلى 5 مئات لأحصل على 15 مئة. (6 = 9 = 15)
الخُْطوَْةُ 4: أَطْرَحُ الُْلوفَ.
أَتَحَقَّقُ مِنْ مَعْقولِيَّةِ الِْإجابَةِ: أُلاحِظُ أَنَّ الِْإجابَةَ 2652 قَريبَةٌ مِنَ الِْإجابَةِ التَّقْديرِيَّةِ 3000 ، إِذَنْ، الِْإجابَةُ مَعْقولَةٌ.
أَتَحَدَّثُ: كَيْفَ أَجِدُ ناتِجَ طَرْحِ عَدَدَيْنِ كُلٌّ مِنْهُما مُكَوَّنٌ مِنْ أَرْبَعِ مَنازِلَ؟
أقوم بترتيب العددين فوق بعضهما، ثم أقوم بطرح كل عدد من العدد الموازي له من نفس المنزلة، وقد أحتاج إلى إعادة التجميع إذا اكان العدد المطروح أكبر من المطروح منه.
مثال إضافي للتوضيح
أطرح 4624 -6587
أُقَدِّرُ:
الخْطوْة 1: أَطْرَحُ الْآحادَ.
الخْطوْةُ 2: أَطْرَحُ الْعَشَراتِ
الخْطوْةُ 3: أَطْرَحُ الْمِئاتِ.
ألاحظ أنه لطرح6 مئات من 5 مئات أعيد تجميع 1 من الألوف إلى 10 مئات وأضيفها إلى 5 مئات لأحصل على 15 مئة. (9 = 6 = 15)
الخُْطوَْةُ 4: أَطْرَحُ الُْلوفَ.
(1= 4 -5) طرح الألوف
أَتَحَقَّقُ مِنْ مَعْقولِيَّةِ الِْإجابَةِ: أُلاحِظُ أَنَّ الِْإجابَةَ 1963 قَريبَةٌ مِنَ الِْإجابَةِ التَّقْديرِيَّةِ 2000، إِذَنْ، الِْإجابَةُ مَعْقولَةٌ.
ولمزيد من التوضيح سوف نحل المثال في أستكشف
487 مترا الفرق بين ارتفاع القمتين.