الفيزياء

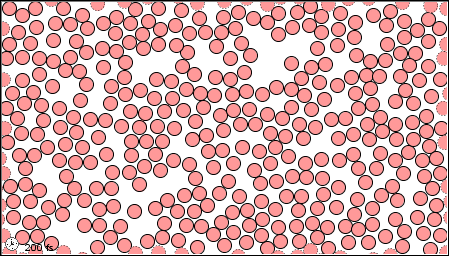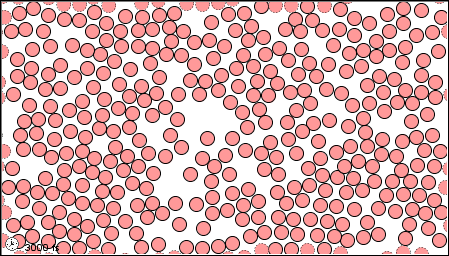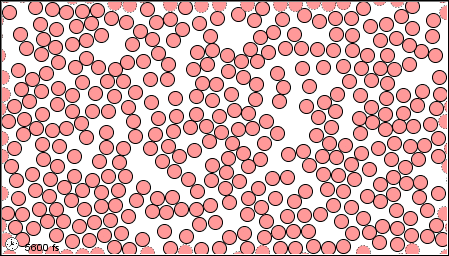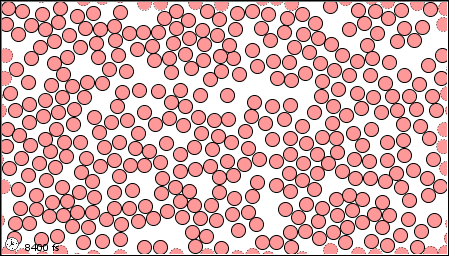
الموائعُ Fluids
درستُ في صفوفٍ سابقةٍ ثلاثَ حالاتٍ

للمادّةِ هيَ الحالةُ الصُّلبةُ والحالةُ السائلةُ

والحالةُ الغازيّةُ.وتعلّمتُ أنَّ ترتيبَ الجُزيئاتِ

داخلَ السوائلِ والغازاتِ،وطبيعةَ الروابطِ

التي تنشأُ بينَ جُزيئاتِها، تُكسبُها القدرةَ على

 الانسيابِ (الجريانِ)، وبذلكَ يتغيّرُ شكلُها؛

فالسوائلُ والغازاتُ ليسَ لها شكلٌ محدَّدٌ،

بلْ تتّخذُ شكلَ الوعاءِ الذي يحتويها. أتأمّلُ

الشكلَ ( 1).

يُطلقُ على الموادِّ التي لها القدرةُ على الجريانِ،

وتغييرِ شكلِها اسمَ موائعَ Fluids ، وبذلكَ فإنَّ

الموائعَ تشملُ السوائلَ والغازاتِ.يعتمدُ سلوكُ

المائعِ وخصائصُه على حالتِه الحركيّةِ، وتُقسمُ 

الموائعُ من حيثُ حالتُها الحركيّةُ إلى قسمينِ هما:

الموائعُ الساكنةُ والموائعُ المتحرّكةُ،

وستقتصرُ دراستُنا في هذهِ الوحدةِ على الموائعِ

 الساكنةِ.

     غاز      سائل       صلب       

الشكل (1)

ضغط المائع الساكن

Pressure of a Static Fluid

تتعرّض أجسامنا طوال الوقتِ إلى ضغط

من الهواء المحيط بنا، يُعرفُ بالضغط الجوي.

نشعر بضغط الماء على أجسامنا عندما نسبحُ

تحت سطح الماء، ويزداد هذا الضغط بزيادة

 العمق.

يُعرَّفُ الضغط Pressure بأنَّه قوةُ عموديّة تؤثر في

 وحدة المساحة، ويُقاسُ بوحدة (N/m) التي تُعرفُ

 بالباسكال (Pa) بحسب النظام  الدولي للوحداتِ.

ويُرمز إلى الضغط بالرمز (P)،  ويُعبر عنه بالعلاقة

 الرياضية الآتية: 

     $\mathit{P}\mathbf{=}\frac{\mathbf{F}}{\mathbf{A}}$

يتأثر الجسم داخل المائعِ بضغط؛ سببه وزن

 المائع فوق الجسمِ.وبزيادة ارتفاع عمودِ المائع

فوق الجسمِ يزداد وزن ذلك المائع، ما يؤدّي إلى

زيادة الضغط المؤثر في الجسم، وهذا يفسر زيادة

الضغط على جسمِ الغواص بزيادة العمق تحت

سطح الماء. ولما كانت جزيئات المائع تتحرك بحرية؛

فَإِنَّ المائعَ يؤثر بضغط في الاتجاهات جميعها في

الأجسام التي بداخله.

 شكل 2

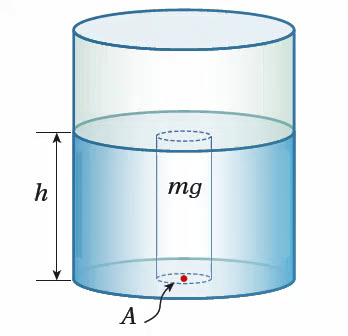
ضغط المائع عند نقطة داخله

Pressure at a Point Inside a Fluid

نقطةً تقعُ داخل مائع ساكن (ماء مثلاً) على

عمق (h) من سطحِه، إنَّ القوة العموديّة

المسببةللضغط عند هذه النقطة، هي وزن

عمودِ الماء (mg) الممتد من سطح الماء

 إلى وحدة المساحة (A) المحيطة بالنقطة.

فإذا كانَ المائعُ سائلاً متجانسا؛ فإن كثافته

 (ص) تكون ثابتةٌ، وللتوصل إلى علاقة لحساب

ضغط السائل عند نقطة

 داخله، أتبع الخطوات الآتية:

-الكتلة تساوي ناتج ضرب الكثافة في الحجم،

لذا فإنَّ كتلة السائل يُعبر عنها بالعلاقة:  

                  $m =\rho V$

 - حجم عمودِ السائل يُعبّر عنه بالمعادلة:

           $V = Ah$

بتعويض الحجم في معادلة الكتلة نتوصل

   إلى أنَّ: 

   $m =\rho Ah$

-بتعويض الكتلة، فإنّ وزن عمود السائل (F)

يساوي:

    $Fg = mg = \rho Ah g$

- من معادلة تعريف الضغط، فإنَّ: 

  $P=\frac{F}{A} = \frac{\rho Ah g}{A} = \rho hg$

مما سبق نتوصل إلى أنَّ ضغط المائع

  Fluid Pressure الساكن  عند  نقطة داخله

وعلى عمق (h) تحت سطحه يُحسبُ مِنَ

 العلاقة الآتية:

    $P_{fluid}= \rho hg$

حيثُ : ($\rho$) كثافة المائع، ($g$) تسارُعُ

 السقوط الحر ومقداره:

       $( 10 m/s^2 \mathrm{تقريبا}) 9.8m/s^2$.

الشكل (3)

    العوامل التي  يعتمد عليها

 ضغط  المائع:

تشير العلاقة $P_{fluid}= \rho hg$) ) إلى أنَّ ضغط

المائع عند نقطة داخله  يتناسب طرديا مع

 كلّ من:

• عمق النقطة داخل المائع 
• كثافة المائع
• تسارع السقوط الحر

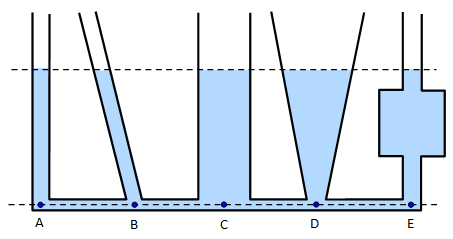
ويكونُ ضغط المائع متساويًا عند النقاط

جميعها التيتقع على العمقِ نفسه من

سطح المائع. ولا يعتمد ضغط المائع على

شكل الوعاء الذي يحتويه، أو مساحة

سطح المائع؛ فمثلًا، في الشكل في الشكل

(4)، يكون ضغط المائع عند النقاط(A) و (B)

و (C) و(D) و(E) متساويًا؛ لأنَّ ارتفاع الماء في

الأوعية متساو.

الشكل (4) 

كذلك فإنَّ السمكتين في الشكل (5)

تتأثران بضغط الماء نفسه في الوعاءين

لأنهُما تسبحان على العمقِ نفسه،ويجدر

الانتباه إلى أنَّ الضغط الذي يُحسبُمن

العلاقة:

             $P_{fluid}= \rho hg$ 

  ضغط المائع فقط، فالسمكة المبيَّنة في

الشكل (5)تتأثر أيضًا بالضغطِ الجوي،

(سأتعرفُ كيفية قياس الضغط الجوي

 في الدرس الثاني).وباستخدام الرمز (_oP)

ليدل على الضغط الجوي عند سطح الماء،

الضغط الكليَّ عند نقطة داخلَ مائع متجانس

يُعبَّر داخل مائع متجانس يعبر عنه بالعلاقة

  الآتية: 

                 $\mathit{P}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{P}}_{\mathbf{o}}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{\rho }\mathit{h}\mathit{g}$

الشكل (5)

مثال محلول

أحسبُ الضغطَ الكلّيَّ المؤثِّرَ في غواصٍّ

يسبحُ في بحيرةٍ على  عمقِ:
     أ) (20m)
   ب) (40m)
   علمًا أنَّ: كثافةَ الماءِ  $(1 \times {10}^3 kg/m^3)$،

 وتسارُعَ السقوطِ الحرّ $(10 m/s^2)$ 

والضغطَ الجويَّ ($1 \times {10}^5 Pa$).

الحل:

لحسابِ الضغطِ الكلّيِّ داخلَ المائعِ  

أستخدمُ العلاقةَ:

                            P = P₀ + ρhg
أ) الضغطُ الكلّيُّ على عمقِ (20 m)   

 $P_1 = 1 \times {10}^5 + (1 \times {10}^3 \times 20 \times 10)$
 

$= 1 \times {10}^5 + 2 \times {10}^5$

$= 3 \times {10}^5 P\mathrm{a \; \; \; \; \; \; \; \; \; \; \; }$

ب) الضغطُ الكلّيُّ على عمقِ (40m)

 $P_2 = 1 \times {10}^5 + (1 \times {10}^3 \times 40 \times 10$

$=1 \times {10}^5 + 4 \times {10}^5$

$= 5 \times {10}^5 Pa$

مثال محلول

أنبوبٌ مملوءٌ بالزئبقِ، إذا كانَ مقدارُ ضغطِ

الزئبقِ عندَ أسفلِ الأنبوبِ $\mathbf{(}\mathbf{1}\mathbf{.}\mathbf{36}\mathbf{ }\mathbf{\times }\mathbf{ }{\mathbf{10}}^{\mathbf{5}}\mathbf{ }\mathit{P}\mathit{a}\mathbf{)}$،

أحسب  ارتفاعَه، علمًا أنَّ كثافةَ الزئبقِ $\mathbf{(}\mathbf{13}\mathbf{.}\mathbf{6}\mathbf{ }\mathbf{\times }\mathbf{ }{\mathbf{10}}^{\mathbf{3}}\mathbf{ }\mathit{k}\mathit{g}\mathbf{/}{\mathit{m}}^{\mathbf{3}}\mathbf{)}$.

الحل

بتطبيقِ العلاقةِ:  $$\begin{gathered} P = \rho hg \\ h =\frac{ P}{\rho g} \end{gathered}$$

$= \frac{1.36 \times {10}^5}{ 13.6 \times {10}^3 \times 10 }= 1 m$

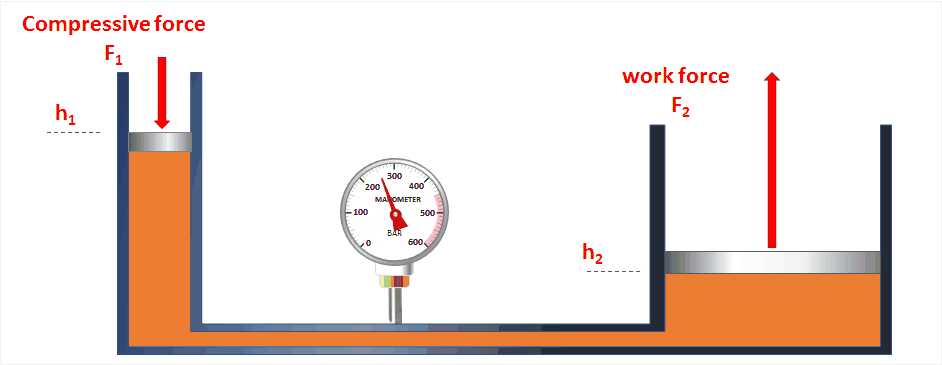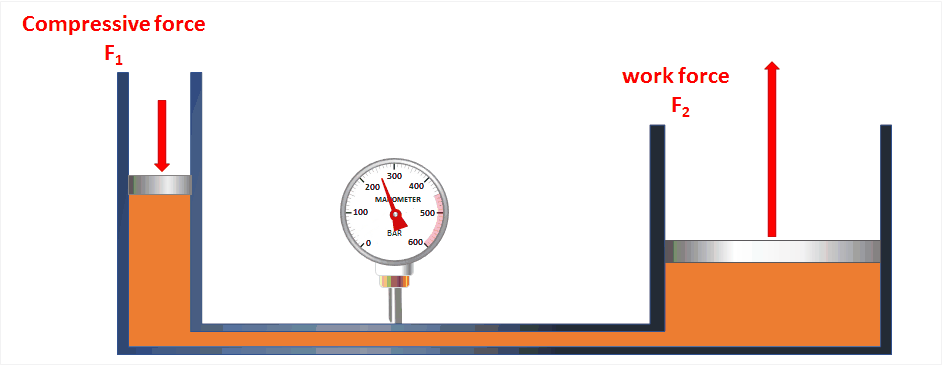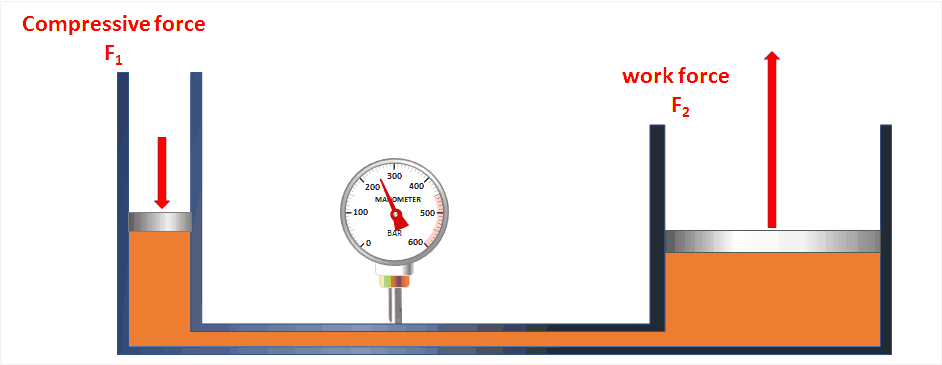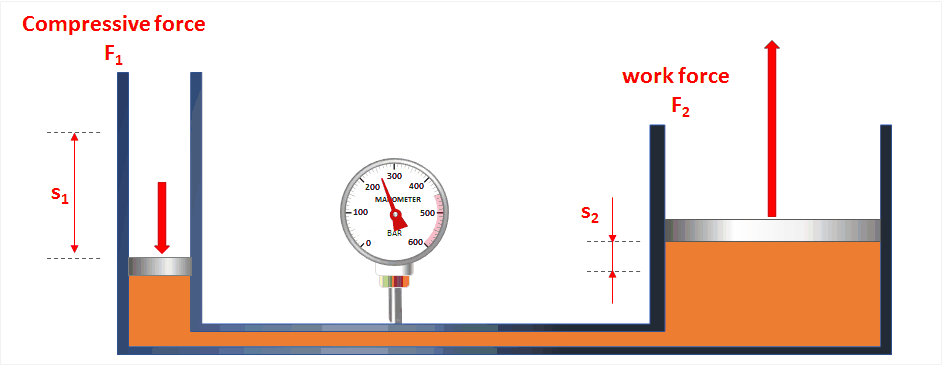
الأنظمة الهيدروليكية Hydraulic Systems

تعلمتُ سابقا أنَّ السائل المحصور إذا

تعرّضَ لضغط خارجي، فإِنَّ هذا الضغط

ينتقل إلى أجزاء السائل جميعها.

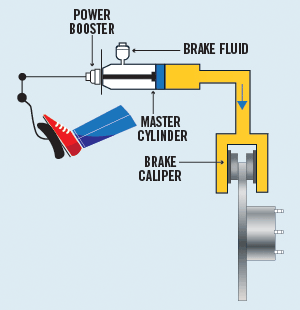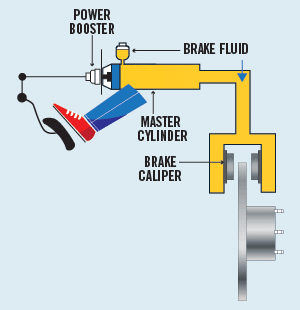
وتعد الروافع الهيدروليكية تطبيقا عمليًّا

على هذه الفكرة، فهي أنظمةٌ تعتمد  في

عملها على استخدام السوائل المحصورة

لنقل الحركةِ. ويبيِّنُ الشكل (6) أمثلة على

روافع  هيدروليكية.

  شكل 6

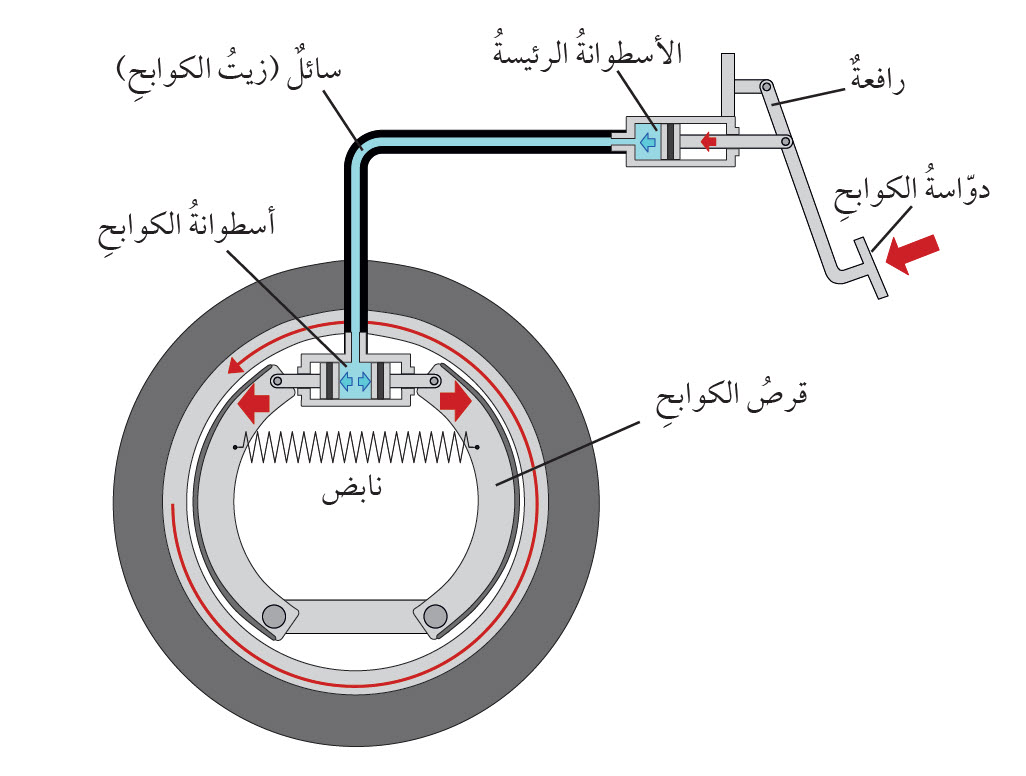
ويُعدُّ نظام الكوابحِ الموجود في السيارة

أحد التطبيقات الشائعة للأنظمة الهيدروليكية.

المخطّط فى الشكل (7) يبيِّنُ الأجزاء الرئيسة

لنظام الكوابح في السيارة. فعندما يضغط

السائق بقدمه على دواسة الكوابح، تدفع

الرافعة المتصلة بالدوّاسة مكبس الأسطوانة

الرئيسة، فينتقلالضغط إلى أجزاء سائل الكوابح

جميعها الذي يملأُ الأسطوانة والأنابيب المتصلة

بها، ليصل إلى أسطوانة الكوابح، فيضغط مكبسا

الأسطوانة على قرص الكوابحنحو الخارج باتجاهين

متعاكسين على نحو ما هو مبين

في الشكل، فينشأ بين الكوابح والإطار قوة احتكاك تؤدّي

إلى إيقاف السيارة.

                                                          شكل 7