المتسلسلات الهندسية اللانهائية
Infinite Geometric Series

فكرة الدرس : إيجاد مجموع المتسلسلة الهندسية اللانهائية المتقاربة.

أولًا : المجاميع الجزئية للمتسلسلة الهندسية الانهائية 

المتسلسلة الهندسية اللانهائية : هي متسلسلة تحوي عددًا لانهائيًّا من الحدود، ويُسمّى مجموع أول n حدًّا من حدود هذه المتسلسلة مجموعًا جزئيًّا ويُرمَز إليه بالرمز ($S_n$) ، وقد يقترب هذا المجموع من قيمة مُحدَّدة.

مثال : 

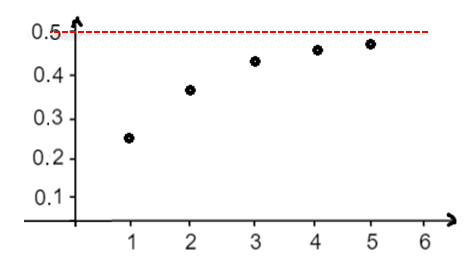
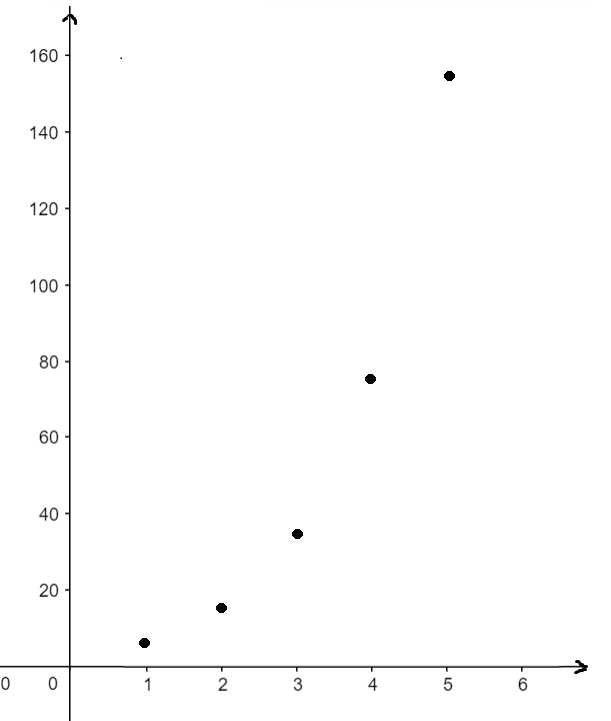
أجد المجاميع الجزئية $S_n$ للقيم : $n = 1 , 2 , 3 , 4 , 5$ ، لكل متسلسلة هندسية لانهائية، ثم أُمثِّلها بيانيًّا : 

1) $\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+...$

 

بتمثيل الأزواج المرتبة :  $(1 , 0.25) , (2 , 0.375) , ( 3 , 0.4375) , (4 , 0.46875) , (5 , 0.484375)$

$$\begin{gathered} S_1 = a_1 = \frac{1}{4} = 0.25 \\ {S}_2 = a_1+ a_2 = \frac{1}{4} + \frac{1}{8} = 0.375 \\ {S}_3 = a_1+ a_2+a_3 = \frac{1}{4} + \frac{1}{8}+ \frac{1}{16} = 0.4375 \\ {S}_4 = a_1+ a_2+a_3+a_4 = \frac{1}{4} + \frac{1}{8}+ \frac{1}{16} + \frac{1}{32}= 0.46875 \\ {S}_5 = a_1+ a_2+a_3+a_4+a_5 = \frac{1}{4} + \frac{1}{8}+ \frac{1}{16} + \frac{1}{32}+ \frac{1}{64}= 0.484375 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

---

 

2) $5 +10 +20 + 40 + 80 + ...$

بتمثيل الأزواج المرتبة :  $(1 , 5) , (2 ,15) , ( 3 , 35) , (4 , 75) , (5 , 155)$

$$\begin{gathered} S_1 = 5 \\ {S}_2 = 5 +10 = 15 \\ {S}_3 = 5 +10 + 20 = 35 \\ {S}_4 = 5 +10 + 20 + 40 = 75 \\ {S}_5 = 5 +10 + 20 + 40 + 80 =155 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

 ثانيًا : مجموع المتسلسلة الهندسية الانهائية المتقاربة 

مفهوم أساسي : 

بالكلمات : تكون المتسلسلة الهندسية اللانهائية متقاربة إذا كانت القيمة المطلقة لأساسها أقل من 1 ، وتكون متباعدة إذا كانت القيمة المطلقة لأساسها أكبر

من أو تساوي 1 

بالرموز  : 

إذا كانت r| <1 | ، فإنَّ المتسلسلة الهندسية اللانهائية تكون متقاربة.        

إذا كانت r| ≥1 | ، فإنَّ المتسلسلة الهندسية اللانهائية تكون متباعدة.      

 

•• إذا كانت المتسلسلة الهندسية اللانهائية متقاربة ، فإنه يُمكن إيجاد مجموعها باستخدام الصيغة الآتية : 

صيغة مجموع المتسلسة الهندسية المتقاربة :    $S_{\infty } = \frac{a_1}{1 - r}$   

أما إذا كانت المتسلسلة الهندسية الانهائية متباعدة فلا يُمكن إيجاد مجموعها . 

 

مثال : 

أُحدِّد إذا كانت المتسلسلات الهندسية اللانهائية الآتية متقاربة أم متباعدة، ثم أجد المجموع للمتقاربة منها :

$\mathit{a}\mathbf{)}\mathbf{ } 1 + \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+...$

الحل : 

أجد قيمة الأساس r بقسمة الحد الثاني على الأول :    $\frac{1}{2}÷ 1 = \frac{1}{2}$  

بما أن : $\left|\frac{1}{2}\right| = \frac{1}{2} < 1$ ، فإن المتسلسلة متقاربة ويُمكن إيجاد مجموعها :

صيغة مجموع المتسلسة الهندسية المتقاربة :       $S_{\infty } = \frac{a_1}{1 - r}$

بتعويض $r = 0.5 , a_1 = 1$                 $S_{\infty } = \frac{1}{1 - 0.5}= \frac{1}{0.5} = \mathbf{ }\mathbf{2}$

إذن مجموع المتسلسلة  = 2 

---

 

$\mathit{b}\mathbf{)} 3+ 9 + 27 + 81 + ...$

الحل : 

أجد قيمة الأساس r بقسمة الحد الثاني على الأول : $9 ÷ 3 = 3$

بما أن : $3 > 1$  ، فإنَّ المتسلسلة متباعدة، ولا يُمكِن إيجاد مجموع حدودها.

---

$\mathit{c}\mathbf{)}\mathbf{ } \sum _{k=1}^{\infty } 2{(0.6)}^{k-1}$

الحل :  

إيجاد الحد الأول $a_1$ بتعويض k = 1 في الحد العام للمتسلسلة : $a_1 = 2{(0.6)}^{1-1 } = 2$

الأساس  1$<$ r = 0.6  ، إذن المتسلسلة متقاربة ، يُمكن إيجاد مجموعها 

صيغة مجموع المتسلسة الهندسية المتقاربة :         $S_{\infty } = \frac{a_1}{1 - r}$

بتعويض $r = 0.6 , a_1 = 2$                       $S_{\infty } = \frac{2}{1 - 0.6} = \frac{2}{0.4} = \mathbf{5}$

إذن مجموع المتسلسلة  = 5

---

 

 ثالثًا : كتابة العدد العشري الدوري في صورة كسر عادي  

يُمكِن استخدام صيغة مجموع المتسلسلة الهندسية اللانهائية لكتابة العدد العشري الدوري في صورة كسر عادي.

مثال : 

أكتب العدد العشري الدوري $0.\overline{23}$  في صورة كسر عادي.

الحل :  

يُمكِن كتابة الكسر العشري الدوري على النحو الآتي :

                                               $0.\overline{23} = 0.232323...$

أيْ إنَّ :

الصيغة التحليلية للكسر العشري               $0.\overline{23 } = 0.23 + 0.0023 + 0.000023 + ...$

بإعادة كتابة الأجزاء العشرية المُتكرِّرة    $0.\overline{23 } = \frac{23}{100} + \frac{23}{10000} + \frac{23}{1000000} + ...$

بوصفها كسورًا عادية .

وهذا يُمثِّل متسلسلة لانهائية ، حدها الأول $a_1 = \frac{23}{100}$ ، ويُمكِن إيجاد أساسها بقسمة الحد الثاني على الحد الأول $\frac{23}{10000}÷\frac{23}{100} = \frac{1}{100}$   

أيْ إنَّ أساس هذه المتسلسلة الهندسية اللانهائية هو : 0.01

بما أنَّ 1 > 0.01 = | 0.01 | ، فإنَّ هذه المتسلسلة متقاربة، ويُمكِن إيجاد مجموعها على النحو الآتي:

صيغة مجموع المتسلسة الهندسية المتقاربة :                    $S_{\infty } = \frac{a_1}{1 - r}$

بتعويض $r = 0.01 , a_1 = 0.23$                       $S_{\infty } = \frac{0.23}{1 -0.01} \frac{0.23}{0.99}=\mathbf{ }\frac{\mathbf{23}}{\mathbf{99}}$  

أيّ أنّ :  $0.\overline{23} = 0.232323... = \frac{23}{99}$  

---