رياضيات

الدرس الثالث: علاقة القسمة بالضرب

 

تمهيد 

تعلمنا في الدرس السابق إيجاد ناتج القسمة كطرح متكرر

أستكشف 

قَسَّمَ أَحْمَدُ 45 كُرَةً زُجاجِيَّةً عَلى أَصْدِقائِهِ. فَإذا أَعْطى كُلَّ واحِدٍ مِنْهُمْ 9 كُراتٍ، فَكَمْ صَديقًا لَهُ؟ 

سوف نتعلم في هذا الدرس طريقة جديدة لإيجاد ناتج القسمة وهو  استعمال العلاقة بين القسمة والضرب لإيجاد ناتج القسمة.

أتعلم 

 الْمَقْسومُ dividend  هُوَ الْعَدَدُ الَّذي يُقْسَّمُ وَيُوَزَّعُ بِالتَّساوي، والْمَقْسومُ عَلَيْهِ  divisor  هُوَ الْعَدَدُ الَّذي يُوَزَّعُ عَلَيْهِ الْمَقْسومُ، وناتِجُ الْقِسْمَةِ  quotient  هُوَ الْعَدَدُ الَّذي يُمَثِّلُ الْإِجابَةَ.

لِكُلِّ جُمْلَةِ قِسْمَةٍ جُمْلَةُ ضَرْبٍ مُرْتَبِطَةٌ بِها؛ لِذا يُمْكِنُني اسْتِعْمالُ حَقيقَةِ الضَّرْبِ الْمُرْتَبِطَةِ بِحَقيقَةِ الْقِسْمَةِ لِأَجِدَ ناتِجَ الْقِسْمَةِ.

 

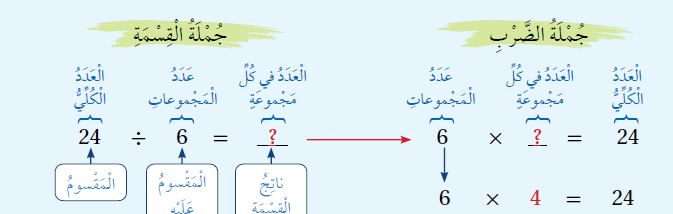
•إِذا قَسَّمْتُ 24 مُكَعَّبًا إِلى 6 مَجْموعاتٍ مُتَساوِيَةٍ، فَكَمْ مُكَعَّبًا في كُلِّ مَجْموعَةٍ؟

ألاحظ أنه لكي أجد ناتج القسمة أستعمل العلاقة مع الضرب؛ فلكي أحصل على ناتج القسمة أضرب المقسوم عليه مع عدد ما ليكون الناتج هو المقسوم.

ففي هذا المثال لكي أحصل على الناتج، علي أن أضرب المقسوم عليه (6) مع عدد ما لكي يكون الناتج هو (24) 

ومن خلال حقائق الضرب يكون هو هذا العدد هو (4) لأن 24 = 4 $\times$ 6

بِما أَنَّ ناتِجَ ضَرْبِ 6 في 4 يُساوي 24 ، إِذَنْ:

$\mathbf{4} = 6 ÷ 24$

---

 

أَتَحَدَّثُ: كَيْفُ تُساعِدُني حَقائِقُ الضَّرْبِ عَلى إيجادِ ناتِجِ الْقِسْمَةِ؟

              لِكُلِّ جُمْلَةِ قِسْمَةٍ جُمْلَةُ ضَرْبٍ مُرْتَبِطَةٌ بِها؛ لِذا يُمْكِنُني اسْتِعْمالُ حَقيقَةِ الضَّرْبِ الْمُرْتَبِطَةِ بِحَقيقَةِ الْقِسْمَةِ لِأَجِدَ ناتِجَ الْقِسْمَةِ.

كي أحصل على ناتج القسمة أضرب المقسوم عليه مع عدد ما ليكون الناتج هو المقسوم.

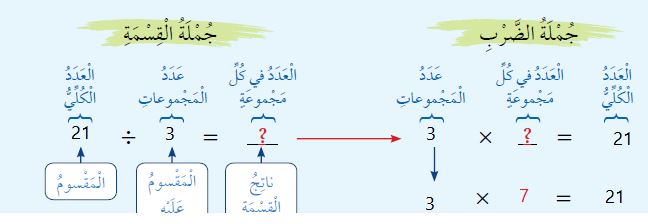
مثال إضافي للتوضيح: أجد ناتج قسمة $= 3 ÷21$:

أستعمل العلاقة بين القسمة والضرب لإيجاد ناتج القسمة كما يلي:

بِما أَنَّ ناتِجَ ضَرْبِ 3 في 7 يُساوي 21، إِذَنْ:

$\mathbf{7} = 3 ÷ 21$

---

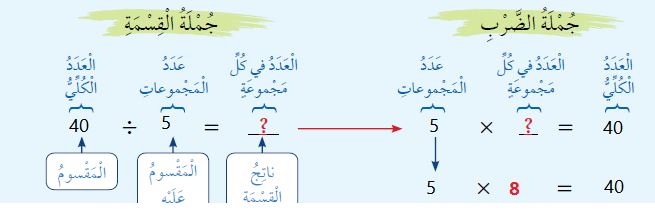
مثال إضافي للتوضيح:  أجد ناتج قسمة $= 5 ÷ 40$

أستعمل العلاقة بين القسمة والضرب لإيجاد ناتج القسمة كما يلي:

بِما أَنَّ ناتِجَ ضَرْبِ 5 في 8 يُساوي 40، إِذَنْ:

$8 = 5 ÷ 40$