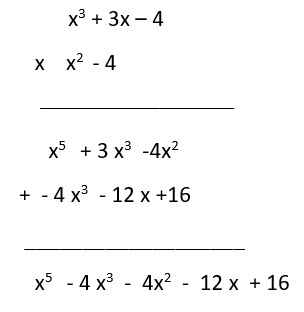رياضيات

اقترانات كثيرات الحدود

نستذكر

• تعريف الاقتران : هو علاقة بين مجموعتين الأولى تمثل المجال والثانية تمثل المدى بحيث يرتبط كل عنصر من عناصر المجموعة الأولى بعنصر واحد فقط من عناصر المجموعة الثانية .
• أنواع الاقترانات التي تم دراستها في الصفوف السابقة

1. الاقتران الثابت ، مثال :         f(x) = 2
2. الاقتران الخطي ،  مثال :        f(x)  = x – 3

سنتعرف على اقتران وحيد الحد و اقتران كثير الحدود

الاقتران وحيد الحد لمتغير واحد

هو اقتران قاعدته عي ناتج ضرب عدد حقيقي يسمى المعامل في متغير أسه عدد صحيح غير سالب

أمثلة :

 

وحيد الحد	2 x3	-23 x 4	$\sqrt{\mathbf{5}}\mathbf{ }{\mathit{x}}^{\mathbf{2}}$	X	9
الأس	3	4	2	1	0
المعامل	2	-23	$\sqrt{\mathbf{5}}$	1	9

 

 

 

 

 

 

نلاحظ ⚠️

• أن جميع الاسس موجبة وصحيحة   
• والمعامل اي عدد حقيقي

 

الاقتران كثير الحدود بمتتغير واحد

هو اقتران يتكون من وحيد حد واحد أو مجموع عدة اقترانات وحيدة الحد بمتغير واحد

أمثلة

1. 1.  f(x) =2x +3
2. 2. F(x) = x² +4x + 5
3. 3. F(x) = -3 x³ +1.2 x⁴ + 5

 

الصورة العامة لكثير الحدود

 

F(x) = an Xn  + a n- 1  X n- 1 + … + a1 X1 + a0

حيث أن

a_n  , a _{n- 1  ,}  … ,  a_{1 ,} a₀           

هي أعداد حقيقية تسمى معاملات كثير الحدود

إذ

a_n   يسمى المعامل الرئيس ، a_n ≠ 0

n درجة كثير الحدود " أكبر أس للحدود"

a₀   يسمى الحد الثابت

 

•  يكون كثير الحدود مكتوبا بالصورة القياسية إذا كانت حدوده  مكتوبة بترتيب تنازلي من أكبرها درجة إلى أصغرها درجة

مثال :

F(X) = 2 x⁴ – x³ +4x +1

---

• كثير الحدود الصفري هو كثير حدود جميع معاملاته أصفار وهو f(x) = 0 وليس له درجة ويمثله المحور x  في المستوى الإحداثي

أمثلة :  

• أحدد إذا كان كل مما يأتي كثير حدود أم لا وفي حال كان كثير حدود أكتبه بالصورة القياسية ثم أحدد المعامل الرئيس و الدرجة والحد الثابت

1. F(x) = 5 + 3x – 4x³ + x⁵

كثير حدود درجته 5 ، صورته القياسية هي   f(x) = x⁵ – 4x³ + 3x + 5    معامله الرئيس 1  ، حده الثابت 5

 

2. F(x) = - 5 x⁴ + 100x + 2x²  - 6 x³ - 11

كثير حدود درجته 4 ، صورته القياسية هي   f(x) =- 5x⁴ – 6x³ + 2 x² + 100x + 11   معامله الرئيس 5 -   ، حده الثابت 11 - 

---

• مجال اي اقتران هو مجموعة القيم التي يأخذها المتغير x والمدى هو مجموعة القيم التي يأخذها المتغير y فكثيرات الحدود مجالها ومداها مجموعة الأعداد الحقيقية ما لم يحدد في السؤال خلاف ذلك
• لتمثيل الاقتران كثير الحدود بيانيا نكون جدولا ، نحدد فيه قيم المتغير x ونحسب قيم f(x)  ثم نعين النقاط ( x , f(X) ) في المستوى الإحداثي واصل بينها بمنحنى متصل

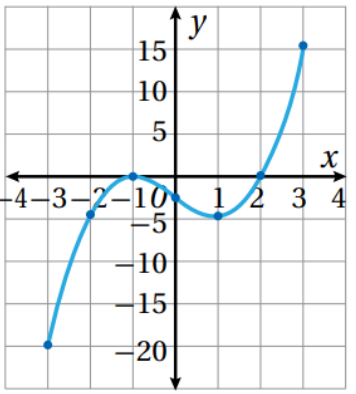
مثال   امثل بيانيا كل اقتران مما يأتي مع تحديد مجاله و مداها

 

1. F(x) = x³ – 3x -2   ,                      -3 ≤ x ≤ 3

الخطوة الأولى : إنشاء جدول

3	2	0	-1	-3	X
16	0	-2	0	-20	Y = f(x)
(3,16)	(2,0)	(0, -2)	(-1 ,0)	( -3-20)	(x,y)

⚠️نأخذ حدود المجال داخل الجدول ⚠

 

 

 

 

 

 

الخطوة الثانية : نعين النقاط في الجدول أعلاه كأزواج مرتبة في المستوى الإحداثي ونصل فيما بينها بمنحنى متصل كما في الشكل المجاور

 

مجال الاقتران : مجموع x  الحقيقية حيث -3 ≤ x ≤ 3   أي

مداه  -20         ≤ y ≤ 16  أي

• لا ننسى أن أصفار الاقتران حسب الشكل هي 1 -   ,  2 

️

---

جمع كثيرات الحدود

لجمع كثيرات الحدود نجمع الحدود المتشابهة التي لها الدرجة نفسها و نجمع معاملاتها

مثال : إذا كان f(x) = x³ + 2 x² – 4  و كان  g(x) = 6x + 2x² + x⁴ + 9  اوجد f(x) + g(x)

F(x) + g(x) =  x³ + 2 x²   – 4  +  6x + 2x² + x⁴  + 9

                   = x⁴  + x³  + ( 2x²  + 2x² ) + 6x + ( -4 +9 )

                    = x⁴  + x³   + 4x²  + 6x + 5

---

طرح كثيرات الحدود

لايجاد ناتج طرح كثيري حدود نحول عملية الطرح إلى جمع النظير الجمعي للمطروح ثم نقوم بعملية الجمع

لايجاد النظير الجمعي فقط نقوم بتغيير اشارة المعاملات

مثال    

   الاقترانF(x) = 2 x² – 3x + 4        è        - f(x)= - 2 x²  + 3x -  4        النظير الجمعي  

مثال على الطرح

يمكن استخدام الطريقة العامودية بحيث يتم ترتيب الحدود المتشابهة تحت بعضها البعض والقيام بعملية الجمع

إذا كان f(x) = 2 x³ + 3x – 4  و كان g(x) = -7x³ + 2 x² + 10   فجد ناتج  f(x) – g(x)

 

F(x) – g(x) =  2 x³ + 3x – 4  - ( -7x³ + 2 x² + 10 )

                  = 2 x³ + 3x – 4  + ( + 7x³ - 2 x² - 10 )

                 =  2 x³ + 3x – 4  + 7x³  -  2 x²     -   10 

                  = 9 x³ + 3x -   2 x²     - 14 

• يمكن استخدام الطريقة العامودية بحيث يتم ترتيب الحدود المتشابهة تحت بعضها البعض والقيام بعملية الجمع

---

ضرب كثيرات الحدود

لضرب كثيرات الحدود نستعمل خاصية توزيع الضرب على الجمع و يمكن ايضا استعمال الطريقة العامودية

مثال : جد ناتج f(x) * g(x)  إذا كان f(x) = x²  - 4  و كان g (x) = x³ + 3x – 4

1. طريقة توزيع الضرب على الجمع

F(x) * g(x) =( x²  - 4) * (x³ + 3x – 4)

                  = ( x² * (x³ + 3x – 4)) + ( -4 * (x³ + 3x – 4))

(( x² *x³⁾   +( x² * 3x ) + (x² *– 4))  + (( -4 *x³) +( -4* 3x ) +(  -4 * – 4 )    =             

                =  x⁵   + 3 x³  -4x²  - 4 x³  - 12 x +16

                =   x⁵   - 4 x³  -  4x²  -  12 x  + 16

 

 

2 ) طريقة الضرب العامودي

---

• تستعمل كثيرات الحدود لتمثيل و حل مسائل حياتية كثيرة في الصناعة والتجارة و الاقتصاد والزراعة والتعليم ومعظم مناحي الحياة

مثال : بلغ عدد المشتركين في مركز لياقة بدنية 840 شخص يدفع كل منهم اشتراكا شهريا مقداره 30 دينار . في دراسة للسوق وجد الباحثون ان المركز سيفقد 25 مشتركا مقابل كل دينار يزيده على قيمة الاشتراك ، فما قيمة الاشتراك التي تحقق للمركز أعلى دخل وما مقدار هذا الدخل ؟

الحل :

نفرض أن المركز جعل قيمة الاشتراك x دينارا حيث أن X > 30      فبالتالي

قيمة زيادة الاشتراك                                                                                            x – 30

عدد المشتركين الذين سيفقدهم المركز                                                                         25 ( x -30)        

عدد المشتركين الباقيين                                                                                                                     = 840 – 25 *( x – 30)

الدخل g(X)   يساوي عدد المشتركين الباقيين                                                                           = g(x) = x ( 840 – 25 ( x – 30 ))

مضروبا بقيمة الاشتراك

  =  840 x – 25 x²   + 750 x  

 -25 x² + 1590 x  

هذا اقتران تربيعي معامله الرئيس سالب أي انه منحنى قطع مكافئ مفتوح للأسفل  وله قيمة عظمى عند رأسه

الإحداثي x  للرأس هو  x = 

إذا قيمة الاشتراك التي تحقق للمركز أعلى دخل هي 31.8 دينار  ومقدار هذا الدخل هو g ( 31.8)

G ( 31.8 ) = -25 ( 31.8 )² + 1590 ( 31.8) = 25218

وذلك باستخدام الآلة الحسابة

إذا أعلى دخل يحققه المركز هو 25218

---