اتحقق من فهمي

• صفحة 9

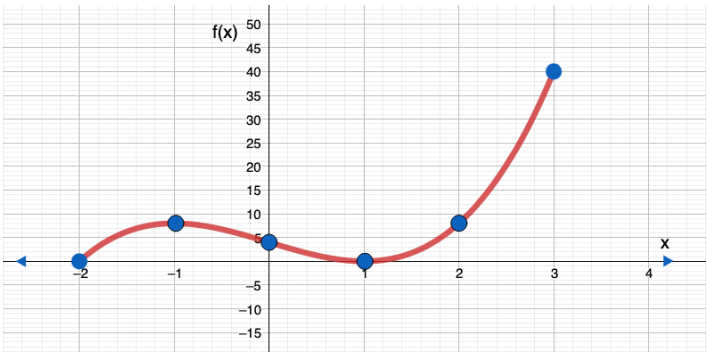
أحدد إذا كان كل مما يأتي كثير حدود أم لا. وفي حال كان كثير حدود أكتبه بالصورة القياسية، ثم أحدد المعامل الرئيس، والدرجة ، والحد الثابت :

الحد الثابت	المعامل الرئيس	الصورة القياسية	درجة كثير الحدود	كثير الحدود	الفرع والمسألة
9	$\sqrt{2}$	H(x) =    $\sqrt{2}$  x5  -5x + 9	5	✔️	A ) h(x)= 9 -5x +  $\sqrt{2}$  x5
✘	✘	✘	✘	✘	B )  F(x) = $\frac{3x + 5 }{x^{2 } + 2 }$ + 2x
0	-2	G(x) = -2x4+18 x3 – 54 x2 +54 x	4	✔️	C )  G(x) = 2x( 3 -x )3
$2\pi$	-7	R(x) = -7 x5  +    $\frac{x^3}{6}$    + $2\pi$	5	✔️	D )  r(x) =    $\frac{x^3}{6}$    - 7x5 +$2\pi$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

توضيح فرع c

G(x) = 2x( 3 -x )³   

         = 2x (  27 -27 x + 9 x²  - x³ )

          = 54 x – 54 x² + 18 x³ – 2 x⁴

ومن ثم نرتيها على الصورة القياسية

 

• صفحة11  

أمثل بيانيا كل اقتران مما يأتي ، محددا مجاله و مداه :

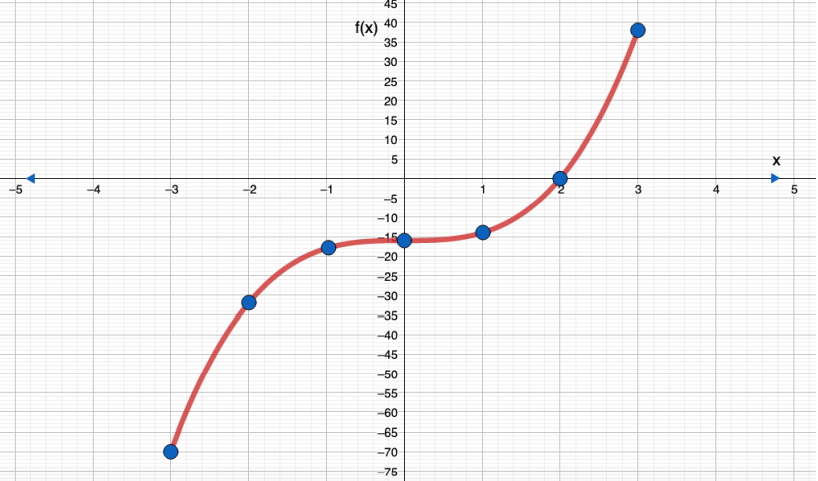
1. F (x) = 2 x³  - 16 ,   -3 ≤ x ≤ 3

 

الحل :

X	-3	-2	-1	0	1	2	3
F(x)	-70	-32	-18	-16	-14	0	38

المجال  $\left[-3 , 3\right]$  

المدى $\left[-70 , 38\right]$

 

 

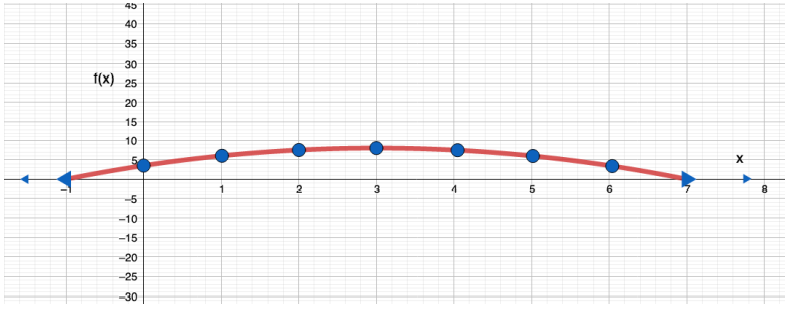
1. F(x) = - 0.5 x²  +3x + 3.5

الحل :

 

X	0	1	2	3	4	5	6
F(x)	$3 \frac{1}{2}$	6	$7 \frac{1}{2}$	8	$7 \frac{1}{2}$	6	$3 \frac{1}{2}$

 

المجال    مجموعة الأعداد الحقيقية 

المدى      $\left\{ y:y \le 8\right\}$

صفحة12

1. إذا كان,  g(x) = -4x³  + 6x²  - 5      f(x) = 3x² + 8x³ +2x +13فأجد f(x) + g(x)

الحل

F(x) + g(x) = 3x² + 8x³ +2x +13  + -4x³  + 6x²  - 5

                  =  9 x²  +4  x³   +2x +8

2. إذا كان  f(x) =  5x³   -12x² + 3x +20 , g(x) = x³  + 6x²  - 14  فأجد g(x) – f(x)

الحل

g(x) – f(x) = x³  + 6x²  - 14 – ( 5x³   -12x² + 3x +20)

                  = x³  + 6x²  - 14 +   - 5x³   +12x² - 3x - 20

                                    = -4 x³  + 18x²  - 3x – 34 

 

• صفحة13

أجد ناتج ضرب f(x) , g(x)  في كل مما يأتي :

 

1. f(x) = 5x²  + 4  , g(x) = 7x +6

الحل

f(x). g(x) = ( 5x²  + 4  ) . ( 7x +6)

 = 35 x³ + 30 x² + 28x +24

 

2. f(x) = 2x³ + x – 8  , g(x) = 5 x² +4x

الحل

    f(x) . g(x) =       ( 2x³ + x – 8  ) . ( 5 x² +4x)

         =  10 x⁵ + 8 x⁴ + 5 x³ +4 x² -40 x²  -32

          =  10 x⁵ + 8 x⁴ + 5 x³  - 36 x²  -32x

• صفحة14

رياضة : يتسع ملعب (ستاد) رياضي لنحو 62000 مشجع. إذا كان ثمن بطاقة الدخول 11 دينارا ، فإن معدل عدد الحضور هو 28000 مشجع . وجدت دراسة أن عدد بطاقات الدخول المبيعة يزيد بمقدار 4000 بطاقة مقابل كل دينار يخصم من ثمن البطاقة . ما ثمن بطاقة الدخول الذي يحقق أعلى دخل ؟ ما مقدار هذا الدخل ؟

الحل

نفرض أن ثمن البطاقة                      x         

قيمة الخصم                                       ( 11 – x )

4000 (11-x)

28000 + 4000(11-x)

  الدخل =x (28000 + 4000 (11-x))

 

 الدخل =28000x  + 44000x - 4000x²

 

 الدخل = 4000x² + 72000x

 

X = $\frac{- b}{2a } = \frac{-72000}{-8000} = 9$          

أعلى دخل   = 4000 (9)² -  72000 ( 9)

أعلى دخل   = 324000

    

---

أتدرب و أحل المسائل صفحة 15 

• أحدد إذا كان كل مما يأتي كثير حدود أم لا . وفي حال كان كثير حدود أكتبه بالصورة القياسية ، ثم أحدد المعامل الرئيس، والدرجة ، والحد الثابت :

الحد الثابت	المعامل الرئيس	الصورة القياسية	درجة كثير الحدود	كثير الحدود	الفرع والمسألة
4	-1	f(x) = – x+4	1	✔️	f(x) = 4 – x
✘	✘	✘	✘	✘	G(x) = $\frac{5 x^{2^{ }} +2x }{ x }$
-12	12	H(x) = 12 x2 -19x -12	2	✔️	H(x) = 3x( 4x- 7) +2x -12
0	5.3	l(x) =  5.3 x3 + 3x2 – 2x	3	✔️	l(x)=3x2+ 5.3 x3– 2x
0	-16	J(t) = -16 t2  +     $\sqrt{7}$ t	2		J(t) =   $\sqrt{7}$ t -16 t2
✘	✘	✘	✘	✘	K(x)=  5  $x^{\frac{3}{2}}$+2x -1
✘	✘	✘	✘	✘	F(x) = 13 (2)x + 6
0	1	F(y) = y7 – 8 y5 +16 y3	7	✔️	F(y) = y3( 4 – y2 )2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

توضيح فرع 3

H(x) = 3x( 4x- 7) +2x -12   

          = 12 x² – 21 x +2x -12

           = 12 x²  - 19 x  - 12 

توضيح فرع 8

F(y) = y³ ( 4 – y² )²

              = y³ ( 16 – 8 y² + y⁴ )

          = 16 y³ – 8 y⁵  + y⁷

•             أمثل كل اقتران مما يأتي بيانيا ، محددا مجاله ومداه :

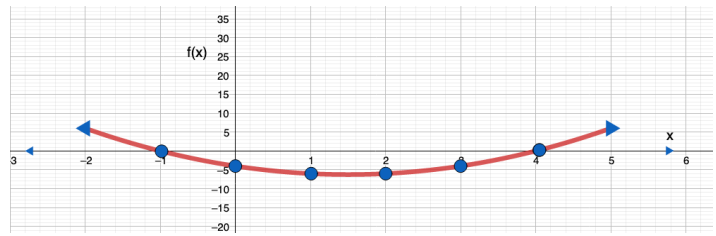
9) f(x) = x² -3x - 4 

       $x = \frac{-b}{2a } = \frac{--3}{2} = \frac{3}{2}$

X	1-	0	1	$\frac{3}{2}$	2	3	4
F(x)	0	4-	6-	$- \frac{25}{4}$	6-	4-	0

المجال : مجموعة الأعداد الحقيقية

المدى  :          $\left\{y : y \ge \frac{-25}{4}\right\}$                    

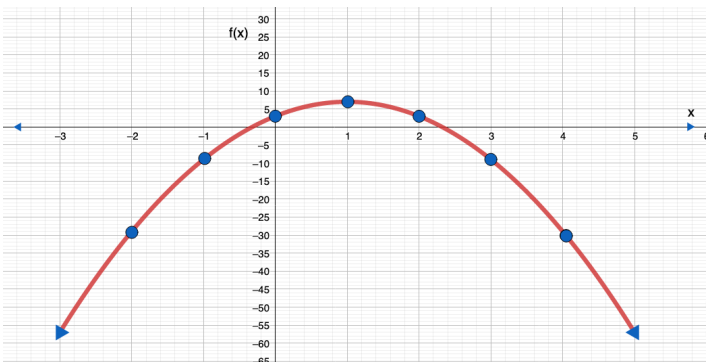
10) f(x) = -4 x² + 8x +3

$x = \frac{-b}{2a } = \frac{-8}{2 (-4)} = \frac{-8}{-8} = 1$

 

X	2-	1-	0	1	2	3	4
F(x)	29-	9-	3	7	3	9-	29-

 

 

المجال : مجموعة الأعداد الحقيقية

المدى  :        $\left\{y : y \le 7\right\}$

                     

11) y = 2x³ - 6x + 4 , -2 ≤ x ≤ 3

 

X	-2	-1	0	1	2	3
F(x)	0	8	4	0	8	40

            المجال :                               [ -2 , 3 ]

                                                   المدى  :      [ 0 , 40]

12) y = 3x²  -  x³ + 9x – 4 , -3 ≤ x ≤ 4

X	-3	-2	-1	0	1	2	3	4
F(x)	23	-2	-9	-4	7	18	23	16

             المجال :                               [ -3 , 4 ]

                                                   المدى  :      [ -9 , 23]

• إذا كان f(x) = 2x +1 , g(x) = 5 x² – 2x³ +4 , h(x) = x⁴ – 5x² +3x – 6  فأجد كل مما يأتي بالصورة القياسية :

13) h(x) + g(x) = x⁴ – 5x² +3x – 6 +5 x² – 2x³ +4

                          =   x⁴  – 2x^{3 +} 3x – 2

14) g(x) – h(x) = 5 x² – 2x³ +4 – ( x⁴ – 5x² +3x – 6)

                          = 5 x² – 2x³ +4 –  x⁴ + 5x² -3x +6

                           = –x⁴  – 2x³  + 10 x² - 3x +10

15) f(x) . h (x) = ( 2x +1 ) . ( x⁴ – 5x² +3x – 6)

                         = ( 2x⁵  -10 x³ + 6x² – 12 x) + ( x⁴ – 5x² +3x – 6)

                          = 2x⁵   +  x⁴   -10 x³ +x² – 9 x – 6

16) x( f(x)) + h(x) = x ( 2x +1) + x⁴ – 5x² +3x – 6

                               = 2 x² + x + x⁴ – 5x² +3x – 6

                                = x⁴  – 3x² +4x – 6

17) ( f(x))² – g(x) = (2x +1)²  - ( 5 x² – 2x³ +4)

                               = (4 x² + 4x +1 ) -5 x² + 2x³ – 4

                               = 2x³ - x² + 4x – 3

18) h(x) – x (g(x)) = x⁴ – 5x² +3x – 6 – x( 5 x² – 2x³ +4)

                                 = x⁴ – 5x² +3x – 6 –5x³ + 2x⁴ - 4x

                                 = 3x⁴ –5x³   – 5x² - x – 6  

19) صــاروخ : أطلق صاروخ إلى أعلى ، وكان ارتفاعه بالأمتار فوق سطح البحر بعد t  ثانية من إطلاقه h(t) = -4.9 t² + 229t +234  أجد أقصى ارتفاع يبلغه الصاروخ .

الحل :

$\frac{-b}{2a} = \frac{- 229 }{2 (-4.9)} = \frac{-229}{-9.8 } = 23.4$

H( 23.4) = -4.9  ( 23.4)² + 229 (23.4) + 234

=  h( 23.4) =  2909.6 أقصى ارتفاع

 

20) زراعة  : وجد مزارع أنه إذا زرع 75 شجرة فاكهة في بستانه ، فإن معدل ما يجنيه من كل شجرة هو 21 صندوقا في الموسم  . وكلما نقص عدد الأشجار شجرة واحدة زاد معدل ما يجنيه من كل شجرة بمقدار 3 صناديق ؛ فتباعد الأشجار بعضها عن بعض يعزز فرصها في الحصول على حاجاتها من التربة. ما عدد الأشجار التي يتعين عليه زراعتها لإنتاج أكبر قدر من الثمر ؟ ما مقدار هذا الثمر ؟

الحل :  

X

( 75 – x)

3 ( 75 – x)

21 + 3 ( 75 – x)

P ( x) = x ( 21 + 3 ( 75 – x) )

P(x) = 21x +225 x – 3 x²

P(x) = – 3 x²  + 264x

$\frac{-b}{2a} = \frac{-246}{2(-3) } = \frac{-246}{-6} =41$

P(41) = -3 (41)² + 246 (41)

P(41) = 5043

 

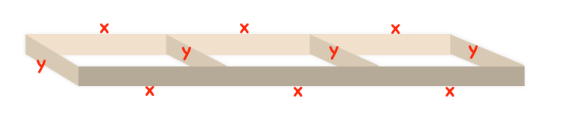
21) سياج   : لدى سعيد 120m من السياج، أراد أن يستعملها لتسييج 3 حظائر مستطيلة متساوية كما في المخطط الآتي. ما أكبر مساحة ممكنة لهه الحظائر ؟

 

 

الحل :  

 

 

 

6x + 4y = 120

3x +2y =60

$$\begin{gathered} y =\frac{60 - 3x }{2 } = 30 - \frac{3}{2 }x \\ A = 3xy \\ A = 3x ( 30 - \frac{3}{2 }x) \\ A = 90x - \frac{9}{2}{x}^2 \\ A= - \frac{9}{2}{x}^2 +90x \\ x = \frac{-b}{2a} = \frac{-90 }{2 ( {\displaystyle \frac{-9}{2}})} = 10 \\ A( 10) = -\frac{9}{2 } {\left(10\right)}^2 + 90 \left(10\right) \\ A\left(10\right) = 450 \end{gathered}$$

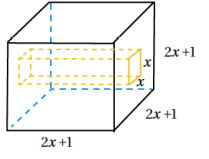
22) هندسة   : مكعب من الخشب، طول ضلعه (2x+1)cm  حفر فيه تجويف مقطعة مربع طول ضلعه  x cm ، وهو يمتد من أحد الأوجه الى الوجه المقابل. أكتب بالصورة القياسية الاقتران الذي يمثل حجم الجزء المتبقي من المكعب.                          

الحل

V = (2x +1)³ – x² ( 2x+1)

V = 8x³ +12x² +6x +1 – 2x³ – x²

V = 6x³ +11x² +6x +1

) ينتج مصنع ثريات عددها x ثريا أسبوعيا، حيث  350 ≤ x ≤ 0 ، و بيبع الواحدة منها بسعر( 150 – 0.3 x) دينارا. إذا كانت تكلفة إنتاج x من الثريات هي ( 6300 +60x -0.1 x² )  دينارا فأجد ربح المصنع من إنتاج x ثريا أسبوعيا وبيعها .

P(x) = x (150 – 0.3 x) - ( 6300 +60x - 0.1 x² )

P(x) = 150x – 0.3 x² -  6300 - 60x +0.1 x²

P(x) =  – 0.2 x² + 90x -  6300

 

مهارات التفكير العليا 

 

24) اكتشف الخطأ   :وجد كل من طه وقاسم ناتج 3x( x² – 2x – 3 ) – ( 5x³ + 7x² – 3 )    :

أحدد إذا كانت إجابة أي منهما صحيحة، مبررا اجابتي .

الحل :

الإجابتين غير صحيحتين

خطأ قاسم عندما جمع -6 x²   مع  -7 x²  فوضع الناتج 6x²

خطـأ طـه لم يضع الاشارة  السالبة قبل القوس الثاني

 

25) مسألة مفتوحة  : اكتب كثيري حدود، أحدهما ذو حدين، و الآخر ثلاثي الحدود، بحيث يكون ناتج ضربهما اقترانا ذا حدين.

الحل :

( x² – x) ( x² + x +1 )

 

26) تحد : أجد أصفار الاقتران : f(x) = x³ – x² – 4x +4

الحل 

F(x) = x² ( x – 1) – 4 ( x – 1)

F(x) = x² – 4 ( x – 1)

F(x) = (x-2) ( x +2 ) ( x – 1)

F(x) = 0

X = 2  , -2 , 1

 

27) تبرير :  إذا كان f , g كثيري حدود ، فاكتب العلاقة بين درجة كل منهما ودرجة كثير الحدود h الناتج من جمعهما وطرحهما وضربهما مبرر إجابتي .

الحل

ليكن f من الدرجة n

ليكن g  من الدرجة m

H = f + g   من الدرجة ( القيمة الأكبر من n , m )

H =f – g  من الدرجة ( القيمة الأكبر من n , m )

لأنه في الجمع والطرح نجمع الحدود المتشابهة

H= f . g  من الدرجة ( n + m)

الضرب لأن الأسس تجمع في حالة الضرب

و بمعنى آخر :

إذا كانت درجة f  أكبر من درجة g فإن ناتج الأكبر (F)

أما إذا كانت درجة f مساوية لدرجة g فإن درجة جمعهما أو طرحهما مساوية لدرجة f أو أقل منها في حالة كان المعاملات لأعلى درجة متساويين في المقدار و مختلفات في الإشارة 

---

كتاب التمارين 

أحدد إذا كان كل مما يأتي كثير حدود أم لا، محددا الدرجة والمعامل الرئيس والحد الثابت لكل كثير حدود ، ثم أكتبه بالصورة القياسية 

الحد الثابت	المعامل الرئيس	الصورة القياسية	درجة كثير الحدود	كثير الحدود	الفرع والمسألة
✘	✘	✘	✘	✘	H(x) = 3x2 +2x-1 +5
-1	-5	$g\left(x\right) = -5x^3+3\frac{1}{5}{x}^2+7x-1$	3	✔️	$g\left(x\right) = 3\frac{1}{5} x^2 - 5x^3 +7x -1$
$\frac{24}{5}$	$-\frac{16}{5}$	$f\left(x\right) =-\frac{16}{5}x +\frac{24}{5}$	1	✔️	$f\left(x\right)=\frac{8( 3-2x)}{5}$
✘	✘	✘	✘	✘	4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أمثل بيانيا كلا مما يأتي ، محددا مجاله ومداه :

5. f(x) = 2x³ - 5 , $-2 \le x \le 3$

المجال $\left[-2 , 3\right]$     المدى  $\left[-21 , 49\right]$

X	-2	-1	0	1	2	3
F(x)	-21	-7	-5	-3	11	49

6. $r\left(x\right) = -x^3 +\frac{3}{2}{x}^2 + 5 , -2\le x\le 2$

المجال                   $\left[-2 , 2\right]$                المدى $\left[3 , 19\right]$

 

X	-2	-1	0	1	2
F(x)	19	7.5	5	5.5	3

7. g(x) = 12 -4x -x² 

             = -x² -4x +12

$\frac{-b}{2a}= \frac{4}{2(-1)}= -2$

     $y \le 16$   : المجال  : مجموعة الأعداد الحقيقية        المدى 

X	-4	-3	-2	0	1
F(x)	12	15	16	12	7

8. h(x) = ( 2x -5)² -10 

             = 4x² -20x +25 -10

           = 4x² -20x +15 

$\frac{-b}{2a }= \frac{20}{2\left(4\right)}= \frac{5}{2}$

المجال   مجموعة الأعداد الحقيقية      المدى $y \ge -10$

X	0	2	$\frac{5}{2}$	3	4
F(x)	15	-9	-10	-9	-1

    

---

إذا كان f(x) = 2x² -4x³ +5x - 1 و g(x) = x³ +5x² - 7  و h(x) = 2x - 4 فأجد ناتج ما يأتي :

9. f(x) +g(x) = (2x² -4x³ +5x - 1  ) + (x³ +5x² - 7)

                   = - 3x³ +7 x² +5x -8 

10. f(x) - g(x) = ( 2x² -4x³ +5x - 1) - (x³ +5x² - 7) 

                     = -5x³ -3x² +5x +6 

11. g(x) - x(h(x)) = (x³ +5x² - 7) - x(2x - 4)

                          = x³ +5x² - 7 - ( 2x² -4x)

                          = x³ +3x² +4x -7 

12. h(x) . f(x) = ( 2x - 4) .(2x² -4x³ +5x - 1)

                   = -8x⁴ +20x³ +2x² -22x +4

13. (h(x))² +f(x) = (2x - 4 )² + (2x² -4x³ +5x - 1)

                        = ( 4x² -16x +16) + 2x² -4x³ +5x -1 

                        = -4x³ +6x² -11x +15

14. f(x). g(x) = (2x² -4x³ +5x - 1) .( x³ +5x² - 7)

                   = -18 x⁵ -4x⁶ +15x⁴ +52x³ -19x²  -35x +7 

15. هل العدد -2 صفر للاقتران h(x) = -x⁴ -5x³ +7x -10 ؟ أبرر إجابتي 

الحل :

$$\begin{gathered} h( -2) = - {( -2)}^4 -5 {(-2)}^3 +7(-2) -10 \\ = -16 -5 ( -8) -14 -10 \\ = -16 +40 -14 -10 \\ = 0 \end{gathered}$$

نعم يعتبر -2 صفر للاقتران h(x) 

---

16. أجد أصفار الاقتران g(x) = ( x- 1)³ -3 ( x -1)² 

الحل :

g(x) = 0

(x -1)² .( x -1 -3) =0

(x -1 )² .(x -4) = 0

     هما أصفار الاقتران x = 1 , x= 4  

---

17.  لدى مزارع 24m  من السياج ، أراد أ، يسيج حظيرة مستطيلة لدواجنه؛ على أن يجعل جدار مخزن في مزرعته أحد جوانب الحظيرة من دون سياج. ما أكبر مساحة ممكنة للحظيرة التي يمكن تسييجها بهذا السياج ؟

الحل 

 طول السياج  24m

المحيط                    x +2y = 24

                   x = 24 - 2y                              

    xy=     المساحة 

xy = ( 24 -2y ) y

f(x) = 24y -2y²     

الاقتران f(x) مفتوح للأسفل له قيمة عظمى عند رأس القطع ، رأس القطع = $\frac{-b}{2a}$

$\frac{-b}{2a} = \frac{-24}{2( -2)} = \frac{24}{4} = 6$

y = 6

x = 24 -12 = 12 

أكبر مساحة = (6) (12)

                          =  72                  

---

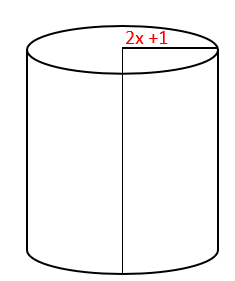
18. يزيد ارتفاع اسطوانة 3 وحدات على طول نصف قطر قاعدتها. أكتب اقترانا يعبر عن حجم الأسطوانة بدلالة x إذا كان طول نصف قطر قاعدتها    (2x +1) وحدة .

( حجم الأسطوانة التي نصف قطرها r ، وارتفاعها h هو $v = \mathrm{\pi } {\mathrm{r}}^2\mathrm{h}$) 

الحل 

 

نصف القطر ( 2x +1 ) 

الارتفاع 2x +4 = 2x +1+3 

الحجم = v                                                        

$$\begin{gathered} v = \mathrm{\pi } {\mathrm{r}}^2 \mathrm{h} \\ = \mathrm{\pi }{( 2\mathrm{x} +1)}^2 ( 2\mathrm{x}+4) \\ = \mathrm{\pi } ( 4{\mathrm{x}}^2 +4\mathrm{x} +1) (2\mathrm{x} +4) \\ = \mathrm{\pi }( 8{\mathrm{x}}^3 +16{\mathrm{x}}^2 +8{\mathrm{x}}^2 +16\mathrm{x} +2\mathrm{x} +4) \\ = \mathrm{\pi }( 8{\mathrm{x}}^3 +24{\mathrm{x}}^2 +18\mathrm{x} +4) \end{gathered}$$

---