الرياضيات

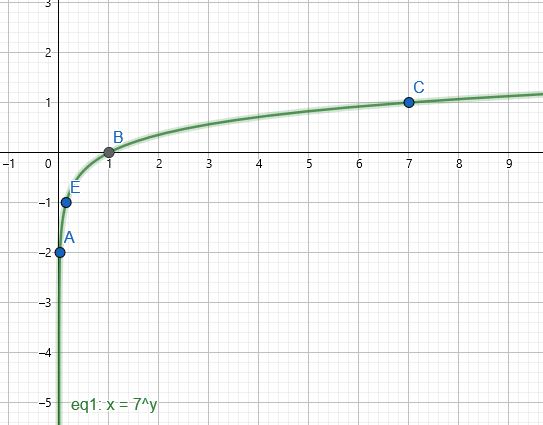
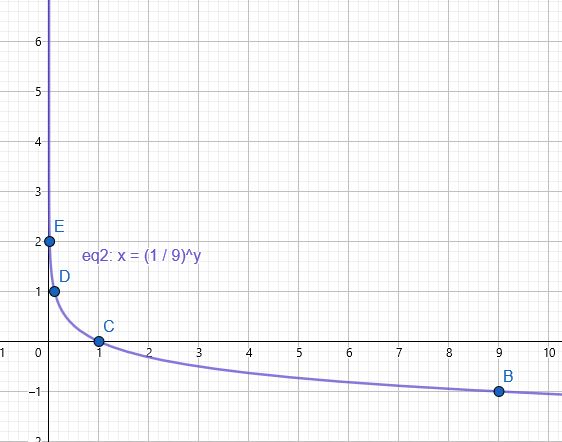
الدرس الثالث: الاقترانات اللوغاريتمية:

 

سنتعرف في هذا الدرس إلى :

1) الاقتران اللوغاريتمي من حيث تعريفه ، والعلاقة بين الصورة الأسية واللوغاريتمية.

2) استعمال تعريف اللوغاريتم في تطبيقات رياضية عدة.

3) الخصائص الأساسية للوغاريتمات.

4) تمثيل الاقتران اللوغاريتمي بيانيًا.

5) مجال الاقتران اللوغاريتمي.

---

أولًا: الاقتران اللوغاريتمي:

 

التعريف: الاقتران اللوغاريتمي للأساس $b$ هو الاقتران العكسي للاقتران الأسي: $f\left(x\right)=b^x$ ، حيث أن: $b>0, b\ne 1$

ويرمز إليه بالرمز: $g\left(x\right)= {\log }_b x$ ، ويُقرأ: لوغاريتم $x$ للأساس $b$

 

 

 

 

 

 

 

 

 

 

 

 

 

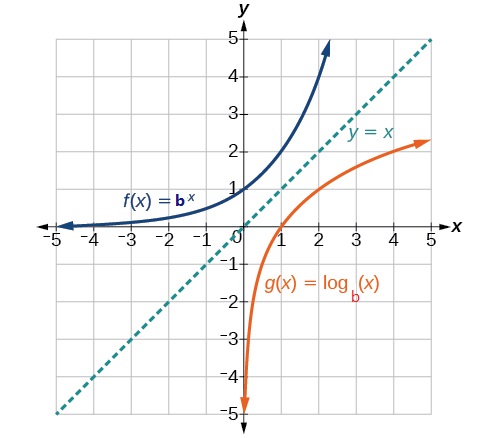
العلاقة بين الصورة الأسية والصورة اللوغاريتمية:

إذا كان $c>0, b>0, b\ne 1$ ؛ فإن:

 

 

 

 

 

 

---

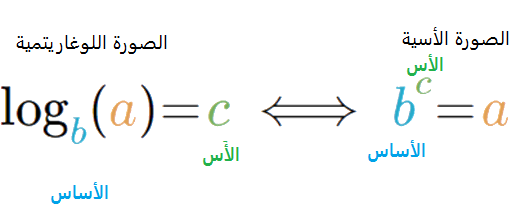
* ثانيًا:استعمال تعريف اللوغاريتم في التحويل بين الصورتين الأسية واللوغاريتمية:

 

يمكن استعمال تعريف اللوغاريتم في تطبيقات رياضية عدة:

 

(أ) لتحويل المعادلة من الصورة اللوغاريتمية إلى الصورة الأسية .

 

مثال: اكتب كل معادلة لوغاريتمية مما يأتي في صورة أسية:

$$\begin{gathered} \mathit{a}\mathbf{)} \mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{4}}\mathbf{ }\mathbf{64}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{3}\mathbf{ }\mathbf{ } \mathit{b}\mathbf{)} \mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{17}}\mathbf{\left(}\mathbf{17}\mathbf{\right)}\mathbf{=}\mathbf{ }\mathbf{1}\mathbf{ } \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathit{c}\mathbf{)}\mathbf{ }\mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{2}}\mathbf{\left(}\frac{\mathbf{1}}{\mathbf{16}}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{-}\mathbf{4}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{d}\mathbf{)}\mathbf{ }\mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{11}}\mathbf{\left(}\mathbf{1}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{0} \end{gathered}$$

 

الحل:

$$\begin{gathered} \mathit{a}\mathbf{)} {\mathbf{4}}^3\mathbf{ }\mathbf{=}\mathbf{64}\mathbf{ }\mathbf{ }\mathbf{ } \mathit{b}\mathbf{)} {\mathbf{17}}^{\mathbf{1}}\mathbf{=}\mathbf{ }\mathbf{17}\mathbf{ } \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathit{c}\mathbf{)}\mathbf{ }{\mathbf{2}\mathbf{ }}^{\mathbf{-}\mathbf{4}}\mathbf{ }\mathbf{=}\frac{\mathbf{1}}{\mathbf{16}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{d}\mathbf{)}\mathbf{ }{\mathbf{11}}^{\mathbf{0}}\mathbf{=}\mathbf{1} \end{gathered}$$

---

(ب) لتحويل المعادلة من الصورة الأسية إلى الصورة اللوغاريتمية.

 

مثال: اكتب كل معادلة أسية مما يأتي في صورة لوغاريتمية:

$$\begin{gathered} \mathit{a}\mathbf{)} {\mathbf{2}}^5\mathbf{ }\mathbf{=}\mathbf{32}\mathbf{ }\mathbf{ } \mathit{b}\mathbf{)} {\mathbf{343}}^{\frac{\mathbf{1}}{\mathbf{3}}}\mathbf{=}\mathbf{ }\mathbf{7}\mathbf{ } \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathit{c}\mathbf{)}\mathbf{ }{\mathbf{6}\mathbf{ }}^{\mathbf{-}\mathbf{2}}\mathbf{ }\mathbf{=}\frac{\mathbf{1}}{\mathbf{36}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{d}\mathbf{)}\mathbf{ }{\mathbf{54}}^{\mathbf{0}}\mathbf{=}\mathbf{1} \end{gathered}$$

الحل:

$$\begin{gathered} \mathit{a}\mathbf{)} \mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{2}}\mathbf{ }\mathbf{32}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{5}\mathbf{ } \mathit{b}\mathbf{)} \mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{343}}\mathbf{ }\mathbf{\left(}\mathbf{7}\mathbf{\right)}\mathbf{=}\mathbf{ }\frac{\mathbf{1}}{\mathbf{3}}\mathbf{ } \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathit{c}\mathbf{)}\mathbf{ }\mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{6}}\mathbf{\left(}\frac{\mathbf{1}}{\mathbf{36}}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{d}\mathbf{)}\mathbf{ }\mathit{l}\mathit{o}{\mathit{g}}_{\mathbf{54}}\mathbf{\left(}\mathbf{1}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{0} \end{gathered}$$

---

(ج) إيجاد قيمة العبارة اللوغاريتمية باستعمال قوانين الأسس:

 

*يمكنك إيجاد قيمة العبارة اللوغاريتمية باتباع الخطوات الآتية:

1) افرض أن المقدار اللوغاريتمي يساوي y

2) اكتب المقدار بالصورة الأسية

3) قم بمساواة الأساسات لتتساوى الأسس

 

مثال: جد قيمة كل مما يأتي دون استخدام الآلة الحاسبة:

$a) {\log }_3\left(243\right) b) {\log }_{15}\left(\sqrt[3]{15}\right) c) {\log }_{144}\left(12\right) d) {\log }_5\left(\frac{1}{625}\right)$

 

الحل:

$b) {\log }_{15}(\sqrt[3]{15})$
${\log }_{15}\left(\sqrt[3]{15}\right) =y$	بافتراض أن المقدار يساوي y
${15}^y = \sqrt[3]{15}$	الصيغة الأسية
${15}^y = {15}^{\frac{1}{3}}$	$\sqrt[3]{15} = {15}^{\frac{1}{3}}$
$y=\frac{1}{3}$	بمساواة الأسس
$\therefore lo{g}_{15}\left(\sqrt[3]{15}\right) =\frac{1}{3}$

$a) {\log }_3(243)$
$lo{g}_3\left(243\right)=y$	بافتراض أن المقدار يساوي y
$3^y = 243$	الصيغة الأسية
$3^y=3^5$	$243 = 3^5$
$y=5$	بمساواة الأسس
$\therefore lo{g}_3\left(243\right) =5$

 

 

 

 

 

 

 

 

 

 

 

 

$d) {\log }_5(\frac{1}{625})$
${\log }_5\left(\frac{1}{625}\right) = y$	بافتراض أن المقدار يساوي y
$5^y =\frac{1}{625}$	الصيغة الأسية
$5^y = \frac{1}{5^4}$	$625=5^4$
$5^y = 5^{-4}$	$\frac{1}{5^4}=5^{-4}$
$y=-4$	بمساواة الأسس
$\therefore lo{g}_5\left(\frac{1}{625}\right) =-4$

$c) {\log }_{144}(12)$
${\log }_{144}\left(12\right) =y$	بافتراض أن المقدار يساوي y
${144}^y = 12$	الصيغة الأسية
${\left({12}^2\right)}^y = 12$	$144={12}^2$
$12{ }^{2y} = 12$	قانون قوة الأسس
$2 y = 1$	بمساواة الأسس
$y=\frac{1}{2}$	بحل المعادلة
$\therefore lo{g}_{144}\left(12\right) =\frac{1}{2}$

 

 

 

 

 

 

 

 

 

 

 

 

---

* ثالثًا: الخصائص الأساسية للوغاريتمات:

إذا كان:$b>0 , b\ne 1$ ؛ فإنّ: $$\begin{gathered} \bullet {\log }_{b }1 =0 , b^0=1 \\ \bullet {\log }_{b }b =1 , b^1=b \\ \bullet {\log }_{b }{b}^x =x , b^x=b^x \\ \bullet b^{{}^{lo{g}_{b}x}} =x, x>0 , lo{g}_{b}x=lo{g}_{b}x \end{gathered}$$

 

* ملاحظة:${\log }_b 0$ غير معرف؛ لأن $b^x\ne 0$ لأي قيمة x

 

مثال: جد قيمة كل مما يأتي دون استخدام الآلة الحاسبة:

$a) {\log }_{4}1 b) {\log }_{14}\left(\sqrt{14}\right) c) {\log }_{24}\left(24\right) d)8^{{\log }_{8}7}$

 

الحل: دون استخدام الآلة الحاسبة وباستخدام الخصائص السابقة يتم إيجاد القيمة:

$a) {\log }_{4}1 =0$	الخاصية الأولى: ${\log }_{b }1 =0$
$$\begin{gathered} b) {\log }_{14}(\sqrt{14}) \\ {\log }_{14}(\sqrt{14}) ={\log }_{14}{\left(14\right)}^{\frac{1}{2}}= \frac{1}{2} \end{gathered}$$	الخاصية الثالثة: ${\log }_{b }{b}^x =x$
$c) {\log }_{24}\left(24\right) =1$	الخاصية الثانية: ${\log }_{b }b =1$
$d)8^{lo{g}_{8}7}=7$	الخاصية الرابعة: $b^{{}^{lo{g}_{b}x}} =x,$

 

---

* رابعًا: تمثيل الاقتران اللوغاريتمي بيانيًا:

لتمثيل الاقتران اللوغاريتمي بيانيًا ، عليك اتباع الخطوات الآتية:

1) استعمل العلاقة العكسية بين الاقتران الأسي واللوغاريتمي لتمثيل الاقتران اللوغاريتمي الذي صورته:$y={\log }_{b}x$ يكافئ $x=b^y$

2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران باختيار قيم للمتغير y ، ثم إيجاد قيم x المرتبطة بها عن طريق التعويض بالمعادلة.

3)  مثل الاقتران في المستوى الإحداثي بتعيين الأزواج المرتبة ، ثم صل بينها بمنحنى متصل

 

مثال: مثل كل اقتران مما يأتي بيانيًا، ثم حدد مجاله ومداه ومقطعيه من المحورين الإحداثيين وخطوط تقاربه، مبينًا إذا كان متناقصًا أم متزايدًا:

$a) {\log }_7 x b) {\log }_{\frac{1 }{9}} x$

 

الحل:

 

$a) {\log }_7 x$

 

1) استعمل العلاقة العكسية بين الاقتران الأسي واللوغاريتمي: ${\log }_7 x =y \to x= 7^y$

2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:

3)  مثل الاقتران في المستوى الإحداثي بتعيين الأزواج المرتبة ، ثم صل بينها بمنحنى متصل :

4) حدد مجاله ومداه ومقطعيه من المحورين الإحداثيين وخطوط تقاربه، مبينًا إذا كان متناقصًا أم متزايدًا:

مجال الاقتران : هو الفترة $(0, \infty )$

مدى الاقتران : هو الأعداد الحقيقية

المقطع x هو 1 (أي يقطع محور x عند النقطة (0, 1)، أي عندما y=0)

لا يقطع محور y  أبدًا ؛ لأن $x>0$ دائمًا.

خط التقارب : الاقتران له خط تقارب رأسي هو المحور y

الاقتران متزايد

---

$b) {\log }_{\frac{1 }{9}} x$

1) ${\log }_{\frac{1 }{9}} x = y \to x= {\left(\frac{1}{9}\right)}^y$

2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:

 

$x={\left(\frac{1}{9}\right)}^y$	81	9	1	$\frac{1}{9}$	$\frac{1}{81}$
y	-2	-1	0	1	2
(x, y)	(81, -2)	(9, -1)	(1, 0)	($\frac{1}{9}$ , 1)	($\frac{1}{81}$ , 2)

3)  تمثيل الاقتران في المستوى الإحداثي:

4) حدد:

مجال الاقتران : هو الفترة $(0, \infty )$

مدى الاقتران : هو الأعداد الحقيقية

المقطع x هو 1 (أي يقطع محور x عند النقطة (0, 1)، أي عندما y=0)

لا يقطع محور y  أبدًا ؛ لأن $x>0$ دائمًا.

خط التقارب : الاقتران له خط تقارب رأسي هو المحور y

الاقتران متزايد

---

* خصائص الاقتران اللوغاريتمي:

يبين التمثيل البياني الآتي الاقتران اللوغاريتمي $f\left(x\right)={\log }_{b}x$ الذي صورته: ، حيث:b عدد حقيقي، $b\ne 1, b>0$ ،

 

 

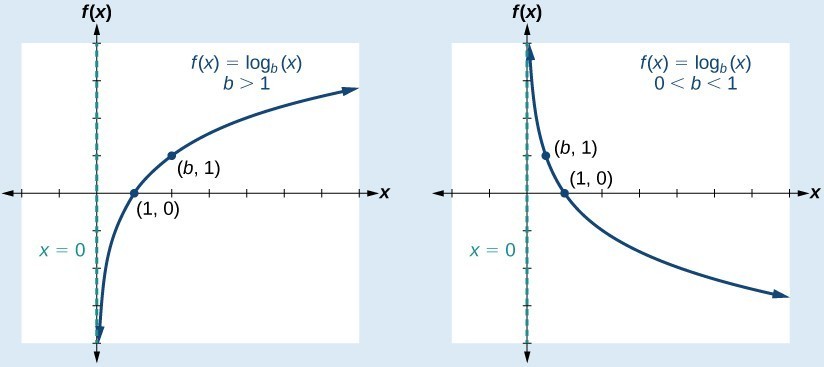
وتتمثل خصائصه فيما يأتي:

• مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة ${\mathrm{ℝ}}^{+}$؛ أي الفترة $(0, \infty )$
• مدى الاقتران : هو مجموعة الأعداد الحقيقية $\mathrm{ℝ}$.
• الاقتران متزايد إذا كان $b>1$
• الاقتران متناقص إذا كان $0 <b <1$
• خط التقارب : يوجد خط تقارب رأسي للاقتران هو المحور y
• الاقتران يقطع المحور x  في نقطة واحدة هي (0, 1) ، ولا يقطع المحور y

---

* خامسًا: مجال الاقتران اللوغاريتمي في صورة : $f\left(x\right)=lo{g}_{b}g\left(x\right)$

مجال الاقتران اللوغاريتمي الذي صورته $f\left(x\right)={\log }_{b}g\left(x\right)$ ، حيث: $b\ne 1, b>0$ هو:

جميع قيم x  في مجال g(x)، التي يكون عندها $g\left(x\right)>0$

 

* خطوات إيجاد مجال الاقتران اللوغاريتمي الذي صورته $f\left(x\right)={\log }_{b}g\left(x\right)$:

1) أنشئ المتباينة g(x) أكبر من صفر  ($g\left(x\right)>0$)

2) قم بحل المتباينة الناتجة وتذكر تغيير اتجاه رمز المتباينة عند الضرب أو القسمة على عدد سالب.

3) جد المجال بتحديد الفترة الناتجة من المتباينة، ويمكنك الاستعانة بخط الأعداد.

 

 

مثال: جد مجال كل اقتران لوغاريتمي مما يأتي، وخط تقاربه الرأسي:

$a) {\log }_7(x+9) b) f\left(x\right)={\log }_6(12-3x)$

 

$a) {\log }_7(x+9)$
$x+9 >0$	$g\left(x\right)>0$
$x>-9$	بحل المتباينة من خلال طرح 9 من الطرفين (الطرح لا يغير رمز التباين).
إذن، مجال الاقتران هو $(-9, \infty )$
خط التقارب الرأسي للاقتران هو $x=-9$

 

$b) f(x)={\log }_6(12-3x)$
$12-3x >0$	$g\left(x\right)>0$
$-3x>-12$	بحل المتباينة بطرح 12 من الطرفين
$x<4$	بقسمة طرفي المتباينة على 3- ، وتغيير اتجاه المتباينة (قسمة طرفي المتباينة على عدد سالب يغير رمز التباين)
إذن، مجال الاقتران هو $(-\infty , 4)$
خط التقارب الرأسي للاقتران هو $x=4$

 

 

 

 

 

 

 

 

 

 

---