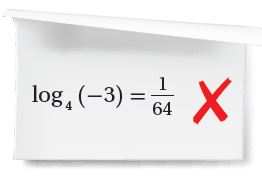مسألة اليوم صفحة 26:
يستعمل الاقتران : لحساب قوة زلزال وفق مقياس ريختر،
حيث شدة الزلزال المراد قياسه، و أقل شدة للزلزال الذي يمكن للإنسان الإحساس به.
ماذا يمثل الرمز في هذا الاقتران؟
الحل:
هو اختصار لكلمة لوغاريتم ويعني معكوس الاقتران الأسي ، فإذا كان فنقول أن لوغاريتم a للأساس هو ، وبالرموز
أتحقق من فهمي 1 صفحة 27:
أكتب كل معادلة لوغاريتمية مما يأتي في صورة أسية:
أتحقق من فهمي 2 صفحة 27:
أكتب كل معادلة أسية مما يأتي في صورة لوغاريتمية:
أتحقق من فهمي 3 صفحة 28:
أجد قيمة كل مما يأتي دون استخدام الآلة الحاسبة:
الحل:
| بافتراض أن المقدار يساوي y | |
| الصيغة الأسية | |
| بمساواة الأسس | |
| بافتراض أن المقدار يساوي y | |
| الصيغة الأسية | |
| بمساواة الأسس | |
| بافتراض أن المقدار يساوي y | |
| الصيغة الأسية | |
| بمساواة الأسس | |
| بافتراض أن المقدار يساوي y | |
| الصيغة الأسية | |
| قانون قوة الأسس | |
| بمساواة الأسس | |
| بحل المعادلة | |
أتحقق من فهمي 4 صفحة 29:
أجد قيمة كل مما يأتي دون استخدام الآلة الحاسبة:
أتحقق من فهمي 5 صفحة 31:
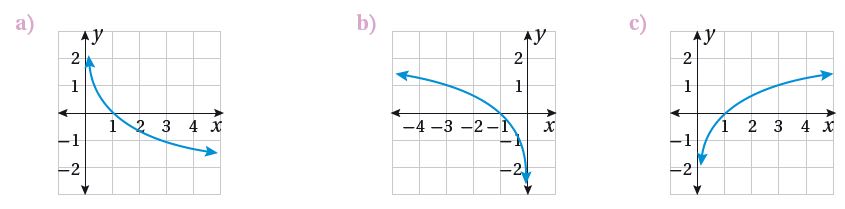
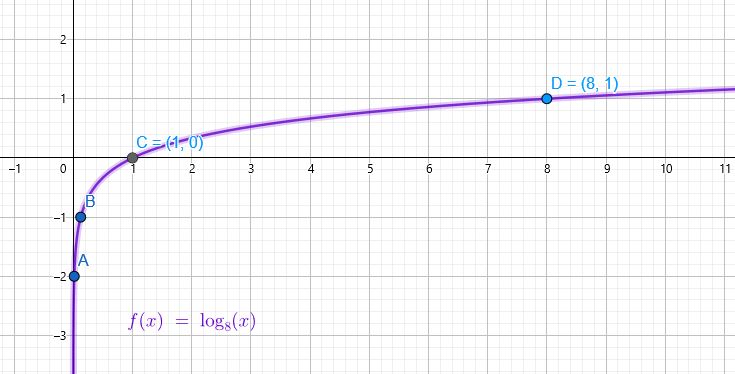
أمثل كل اقتران مما يأتي بيانيًا، ثم أحدد مجاله ومداه ومقطعيه من المحورين الإحداثيين وخطوط تقاربه، مبينًا إذا كان متناقصًا أم متزايدًا:
الحل:
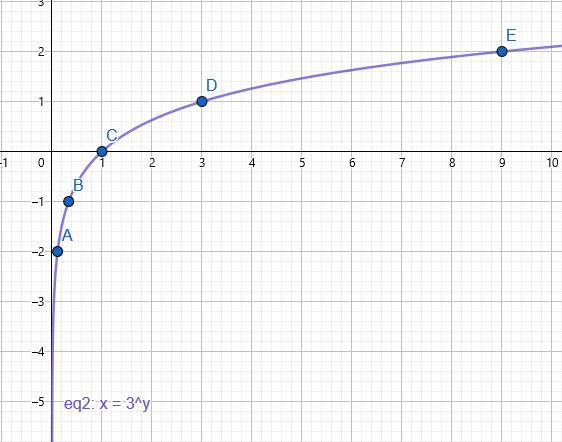
1) استعمل العلاقة العكسية بين الاقتران الأسي واللوغاريتمي:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 1 | 3 | 9 | |||
| y | -2 | -1 | 0 | 1 | 2 |
| (x, y) | (, -2) | (, -1) | (1, 0) | (3, 1) | (9, 2) |
3) مثل الاقتران في المستوى الإحداثي بتعيين الأزواج المرتبة ، ثم صل بينها بمنحنى متصل :
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو مجموعة الأعداد الحقيقية
المقطع x هو 1 (أي يقطع محور x عند النقطة (0, 1)، أي عندما x=1)
لا يوجد مقطع y ؛ لأن دائمًا.
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
1)
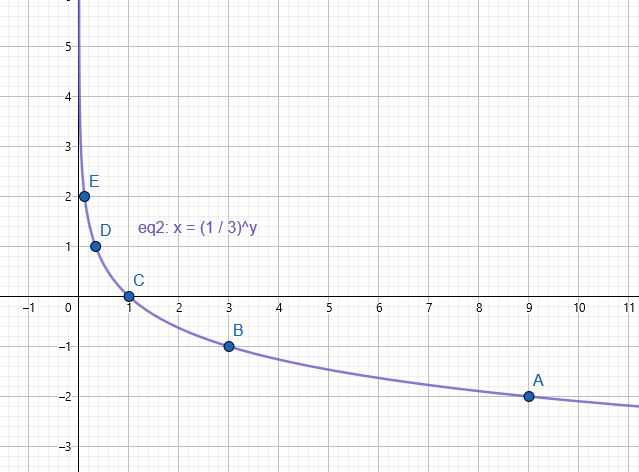
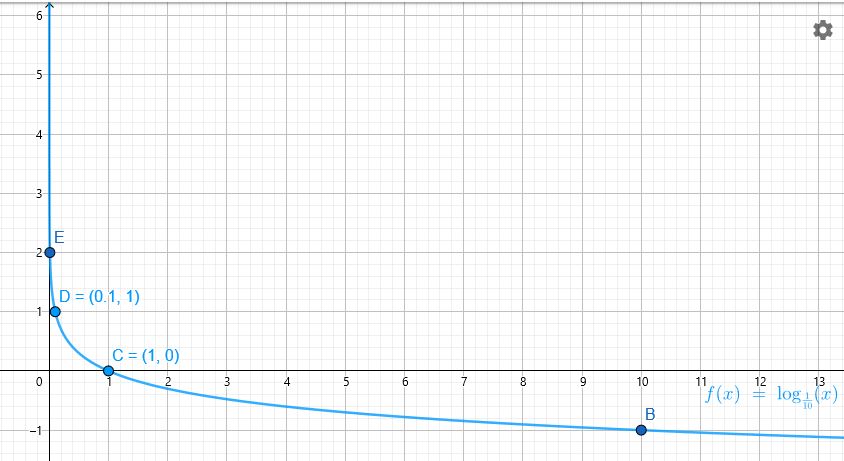
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 9 | 3 | 1 | |||
| y | -2 | -1 | 0 | 1 | 2 |
| (x, y) | (9, -2) | (3, -1) | (1, 0) | (, 1) | (, 2) |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو الأعداد الحقيقية
المقطع x هو 1 (أي يقطع محور السينات x عند النقطة (0, 1)، أي عندما x=1)
لا يوجد مقطع y .
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متناقص
أتحقق من فهمي 6 صفحة 33:
أجد مجال كل اقتران لوغاريتمي مما يأتي:
| بحل المتباينة من خلال طرح 5 من الطرفين | |
|
بقسمة طرفي المتباينة على 1- ، وتغيير اتجاه المتباينة (قسمة طرفي المتباينة على عدد سالب يغير رمز التباين) |
|
| إذن، مجال الاقتران هو الفترة | |
| بحل المتباينة من خلال طرح 9 من الطرفين | |
|
بقسمة طرفي المتباينة على 3 (قسمة طرفي المتباينة على عدد موجب لا يغير رمز التباين) |
|
| إذن، مجال الاقتران هو الفترة | |
أتدرب وأحل المسائل صفحة 33:
أكتب كل معادلة لوغاريتمية مما يأتي في صورة أسية:
أكتب كل معادلة أسية مما يأتي في صورة لوغاريتمية:
أجد قيمة كل مما يأتي من دون استخدام الآلة الحاسبة:
| بافتراض أن المقدار يساوي y | |
| الصيغة الأسية | |
| بمساواة الأسس | |
| بافتراض أن المقدار يساوي y | |
| الصيغة الأسية | |
| قانون قوة الأسس | |
| بمساواة الأسس | |
| بحل المعادلة | |
(طريقة أخرى)
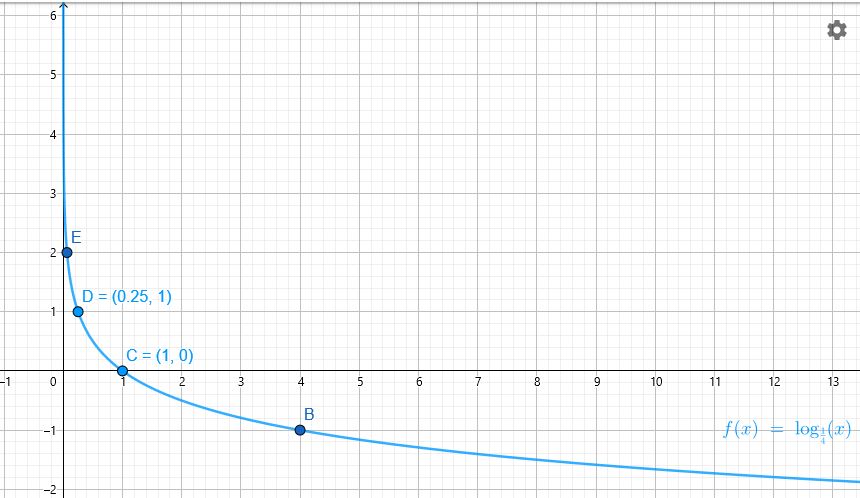
أمثل كل اقتران مما يأتي بيانيًا، ثم أحدد مجاله ومداه ومقطعيه من المحورين الإحداثيين وخطوط تقاربه، مبينًا إذا كان متناقصًا أم متزايدًا:
1) الصورة الأسية:
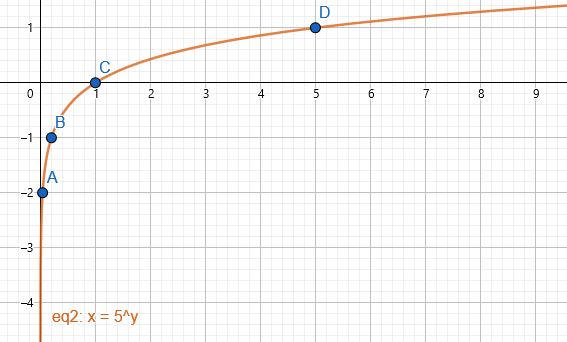
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 1 | 5 | 25 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو مجموعة الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
1) الصورة الأسية:
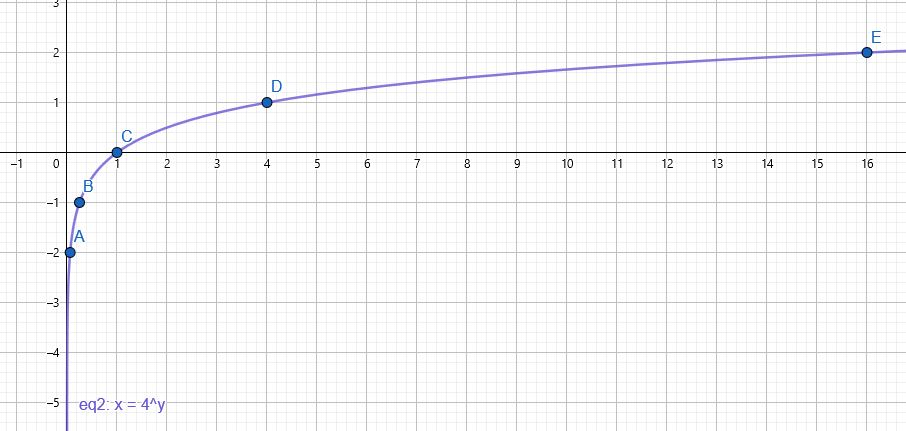
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 1 | 4 | 16 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y أبدًا
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
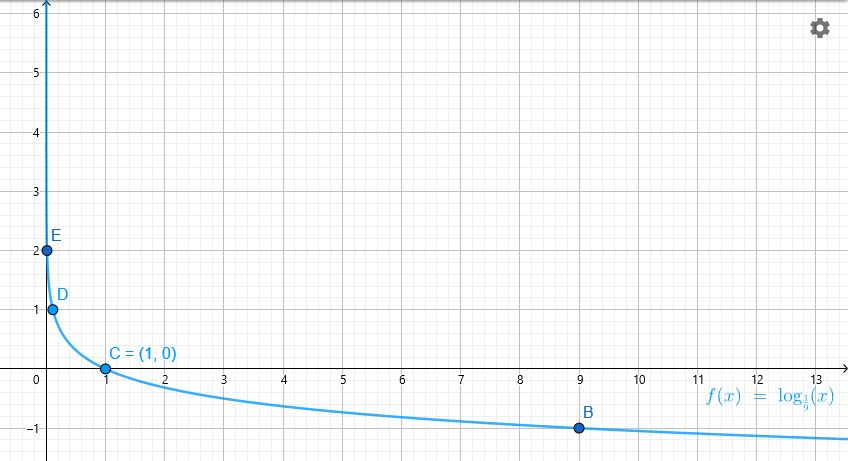
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 25 | 5 | 1 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
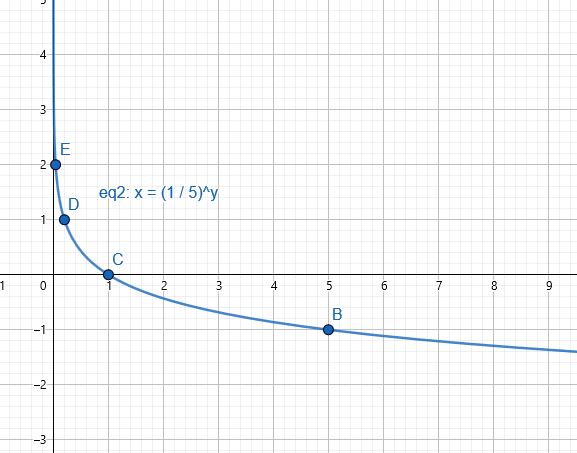
مجال الاقتران :هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متناقص
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 64 | 8 | 1 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
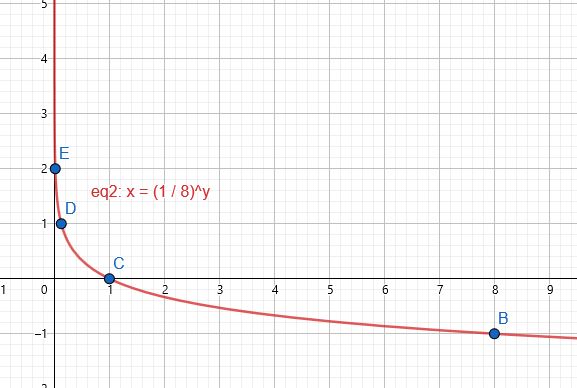
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متناقص
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 10 | 100 | ||||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
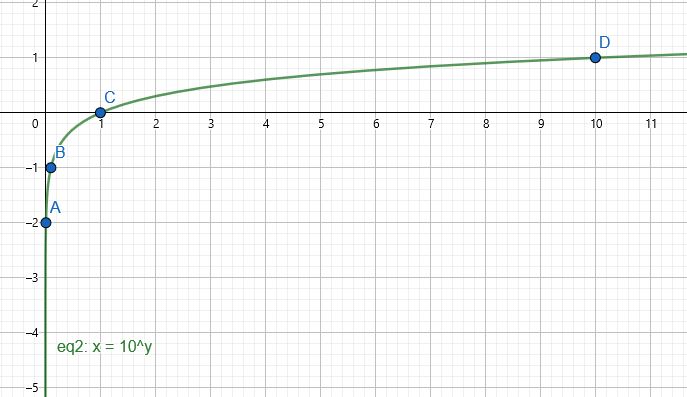
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 1 | 6 | 36 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
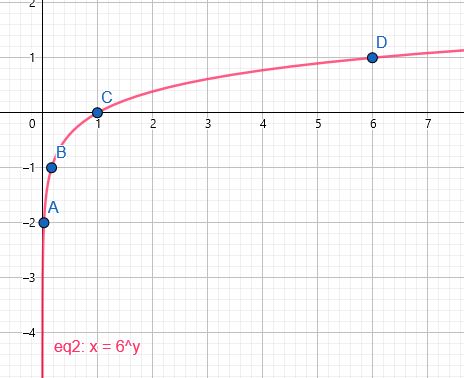
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة أي
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
أجد مجال كل اقتران لوغاريتمي مما يأتي:
الحل :
34) أجد قيمة التي تجعل منحنى الاقتران: يمر بالنقطة .
الحل :
| عوض النقطة بالاقتران حيث: | |
| الاقتران المعطى | |
| بتعويض النقطة بالاقتران | |
| الصورة الأسية | |
| إذا تساوت الأسس تتساوى الأساسات | |
35) أجد قيمة التي تجعل منحنى الاقتران: يمر بالنقطة .
| الاقتران المعطى | |
| بتعويض | |
| بتعويض | |
| الصورة الأسية | |
| بحل المعادلة | |
| قيمة موجبة لأن أساس اللوغاريتم لا يكون سالبًا |
إعلانات: يمثل الاقتران: مبيعات شركة (بآلاف الدنانير) من منتج جديد،
حيث المبلغ (بمئات الدنانير) الذي تنفقه الشركة على إعلانات المنتج.
وتعني القيمة: أنَّ إنفاق على الإعلانات يحقق إيرادات قيمتها من بيع المنتج:
36) أجد 37) أفسر معنى القيم التي أوجدتها في الفرع السابق
الحل :
| الاقتران المعطى | |
| بتعويض a=4 بالاقتران | |
| بالتبسيط حيث | |
|
التفسير: إنّ إنفاق JD 400 على الإعلانات يحقق إيرادات قيمتها JD 30000 من بيع المنتج. |
|
| الاقتران المعطى | |
| بتعويض a=24 بالاقتران | |
|
بالتبسيط حيث:
|
|
|
التفسير: إنّ إنفاق JD 2400 على الإعلانات يحقق إيرادات قيمتها JD 50000 من بيع المنتج. |
|
| الاقتران المعطى | |
| بتعويض a=4 بالاقتران | |
|
بالتبسيط حيث: |
|
|
التفسير: إنّ إنفاق JD 12400 على الإعلانات يحقق إيرادات قيمتها JD 70000 من بيع المنتج. |
|
مهارات التفكير العليا:
تبرير: أكتب بجانب كل اقتران مما يأتي رمز تمثيله البياني المناسب، مبررًا إجابتي:
الحل :
| الاقتران | رمز التمثيل البياني | التبرير |
|
اقتران لوغاريتمي متزايد حيث مجاله ، ويمر منحناه بالنقطة حيث:
|
||
|
الاقتران اللوغاريتمي مجاله: ويمر منحناه بالنقطة حيث: ويمكن استخدام صورته الأسية:
وتظهر هذه الأزواج المرتبة بالتمثيل البياني b |
||
|
الاقتران اللوغاريتمي متناقص ، مجاله ، ويمر منحناه بالنقطة حيث: |
تحدٍّ : أجد مجال كل اقتران لوغاريتمي مما يأتي، محددًا خط (خطوط) تقاربه الرأسي:
الحل :
| لجميع الأعداد الحقيقية عدا الصفر | |
| مجال الاقتران اللوغاريتمي : | |
| خط التقارب الرأسي المحور y | |
|
ملاحظة: يمكن إيجاد المجال من خلال: 1) إيجاد أصفار المعادلة التربيعية (x=0) 2) تمثيل حلول المعادلة على خط الأعداد(خطوط التقارب). 3) تحديد إشارة الأعداد على يمين ويسار الحلول بتعويض عدد مثلًا على كل جهة لتحديد إشارة الاقتران.
4) فيكون المجال جميع الأعداد الحقيقية عدا الصفر : |
|
| بحل المتباينة التربيعية | |
|
|
مجال الاقتران اللوغاريتمي موجب دائمًا أكبر من صفر (استخدم خط الأعداد لتحديد الإشارات) |
|
خطوط التقارب الرأسي: (جذرا المعادلة التربيعية ) |
|
43) أكتشف الخطأ : كتبت منى المعادلة الأسية: في صورة لوغاريتمية كما يأتي:
أكتشف الخطأ الذي وقعت فيه منى، ثم أصححه.
الحل :
الصورة اللوغاريتمية هي ، بحيث أن
إذن الخطأ هو وجود () بالصورة اللوغاريتمية، حيث يجب أن تكون أكبر من صفر ()
والأس يصبح الناتج بالصورة اللوغاريتمية
التصحيح:
الصورة الأسية هي :
الصورة اللوغاريتمية:
كتاب التمارين صفحة 11:
أكتب كل معادلة لوغاريتمية مما يأتي في صورة أسية:
أكتب كل معادلة أسية مما يأتي في صورة لوغاريتمية:
أجد قيمة كل مما يأتي دون استخدام الآلة الحاسبة:
أمثل كل اقتران مما يأتي بيانيًا، ثم أحدد مجاله ومداه ومقطعيه من المحورين الإحداثيين وخطوط تقاربه، مبينًا إذا كان متناقصًا أم متزايدًا:
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 1 | 8 | 64 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متناقص
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 16 | 4 | 1 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متناقص
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
| 81 | 9 | 1 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متناقص
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
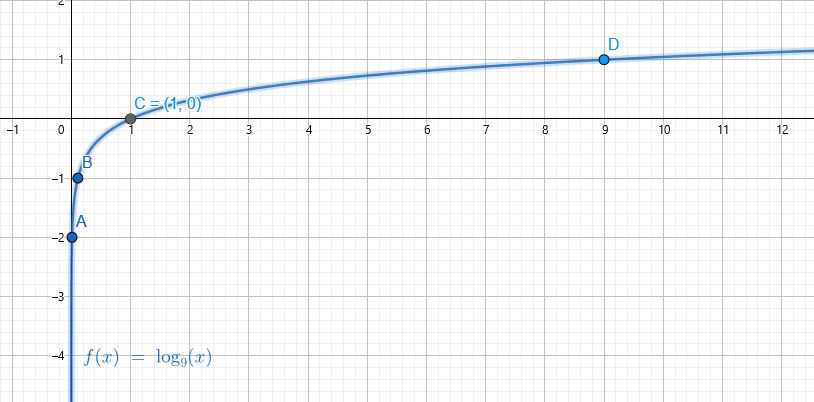
| 1 | 9 | 81 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
1) الصورة الأسية:
2) أنشئ جدولًا للقيم لإيجاد الأزواج المرتبة اللازمة لتمثيل الاقتران:
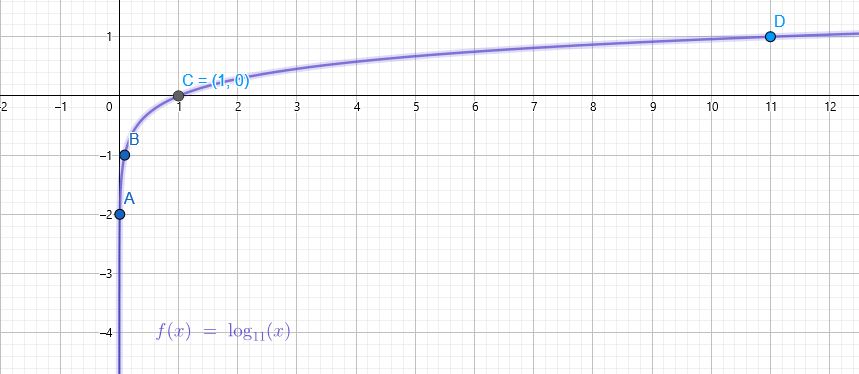
| 1 | 11 | 121 | |||
| y | -2 | -1 | 0 | 1 | 2 |
3) تمثيل الاقتران في المستوى الإحداثي:
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة
مدى الاقتران : هو الأعداد الحقيقية
المقاطع : المقطع x هو 1
لا يوجد مقطع y
خط التقارب : الاقتران له خط تقارب رأسي هو المحور y
الاقتران متزايد
أجد مجال كل اقتران لوغاريتمي مما يأتي:
الحل:
34) ضوء: تمثل المعادلة: العلاقة بين شدة الضوء بوحدة lumen والعمق بالأمتار في إحدى البحيرات.
كم تبلغ شدة الضوء عند عمق ؟
الحل:
| المعادلة المعطاة | |
| بتعويض | |
| الصورة الأسية | |
| بالضرب التبادلي | |
| باستخدام الآلة الحاسبة |
تبلغ شدة الضوء عند عمق تقريبًا: