رياضيات

الانسحابُ في الْمُسْتَوى الِْإحْداثِيِّ

فكرة الدرس : أرسم انسحابًا على المستوى الإحداثي.

المصطلحات : الانسحاب، الصورة.

الانسحاب : هو انتقال الشكل من مكان إلى آخر من دون تغيير أبعاده أو تدويره، ويُطلق على الشكل الناتج من الانسحاب اسم (الصورة).

                                            

مثال  1

أصف كل انسحاب مما يأتي معتمدًا على الشكل الآتي:

1) $A \to D$                          2) $C \to D$ 3) $E \to C$                         4) $B \to E$

 

 

 

 

 

 

 

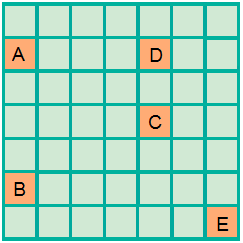الحل :

انسحاب 4 وحدات إلى اليمين .	1) $A \to D$
انسحاب وحدتين إلى الأعلى .	2) $C \to D$
انسحاب وحدتين إلى اليسار و 3 وحدات إلى الأعلى .	3) $E \to C$
انسحاب 6 وحدات إلى اليمين ووحدة واحدة إلى الأسفل.	4) $B \to E$

 

 

 

 

 

 

---

لعمل انسحاب شكل بمقدار  a  وحدة أفقيا ، و b   وحدة رأسيا على المستوى الإحداثي، أحرك كل رأس من رؤوسه بمقدار  a  وحدة أفقيا، و  b  وحدة

رأسيا.

مثال : 

أرسم المثلث ABD الذي إحداثيات رؤوسه : $A (-4 , 4) , B (1 , 2) , C (-2 , 1)$ ، ثمّ أجد إحداثيات رؤوسه تحت تأثير انسحاب 3 وحدات إلى اليمين و 6 وحدات إلى الأسفل . 

الحل : 

الخطوة 1 أرسم المثلث على المستوى الإحداثي.   أحدد النقاط التي تمثل رؤوس المثلث على المستوى الإحداثي.    أصل بين النقاط  لرسم المثلث.
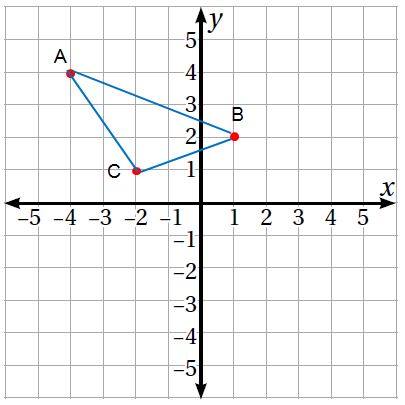الخطوة 2 أسحب رؤوس المثلث. أسحب كل من رؤوس المثلث 3 وحدات إلى اليمين، و  6  وحدات إلى الأسفل. أي إن إحداثيات رؤوس الصورة هي :   $A\text{'} (-1 , -2) , B\text{'} (4 , - 4) , C\text{'} (1 , -5)$

 

 

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

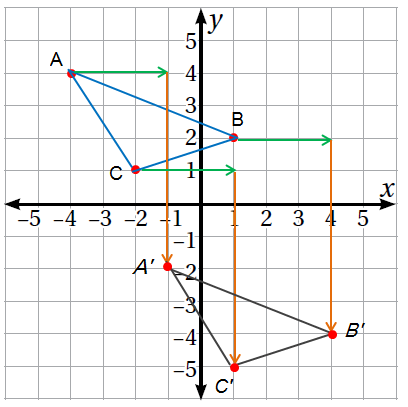• يُمكن إيجاد قاعدة عامة  ، واستعمالها لتحديد صورة نقطة على المستوى الإحداثي تحت تأثير انسحاب مُعطى من دون أن أرسم.

مفهوم أساسي ( انسحاب زوج مرتب على المستوى الإحداثي)  بالكلمات لعمل انسحاب للزوج المرتب ( x , y ) بمقدار  a وحدة أفقيًا، و b وحدة رأسيًا على المستوى الإحداثي ، أجمع a  مع الإحداثي x، و b مع الإحداثي  .y  بالرموز  : $(x , y) \to (x+a , y + b)$ إذا كانت $a$  موجبة فالانسحاب إلى اليمين، وإذا كانت سالبة فالانسحاب إلى اليسار. إذا كانت $b$ موجبة فالانسحاب إلى الأعلى، وإذا كانت سالبة فالانسحاب إلى الأسفل.

 

 

 

 

 

 

 

 

 

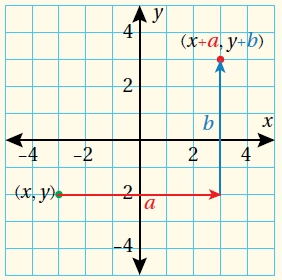مثال 

أجد إحداثيات صور النقاط المعطاة في ما يأتي تحت تأثير انسحاب مقداره 3 وحدات إلى اليمين ، و 5 وحدات إلى الأسفل:

1) A (2 , 3)                                     2) B (7 , 0)                                    3) C (4 , -6)                    

الحل : 

1) A (2 , 3) 

قاعدة الانسحاب	$(x , y) \to (x+3 , y-5)$
أعوض الإحداثيين	$A (2 , 3) \to A\text{'} (2 + 3 , 3 -5)$
إحداثيا الصورة	$A (2 , 3) \to A\text{'} (5 ,-2)$

 

 

 

 

 

 2) B (7 , 0) 

قاعدة الانسحاب	$(x , y) \to (x+3 , y-5)$
أعوض الإحداثيين	$B (7 , 0) \to B\text{'} (7 +3 , 0 -5)$
إحداثيا الصورة	$B (7 , 0) \to B\text{'} (10 ,-5)$

 

 

 

 

 3) C (4 , -6) 

قاعدة الانسحاب	$(x , y) \to (x+3 , y-5)$
أعوض الإحداثيين	$C (4 , -6) \to C\text{'} (4 +3 , -6 -5)$
إحداثيا الصورة	$C (4 , -6) \to B\text{'} (7 ,-11)$

 

 

 

 

 

 

---

 

• يمكن تحديد قاعدة الانسحاب الذي ينقل شكل إلى صورته على المستوى الإحداثي، وذلك بتحديد المسافة الأفقية والمسافة الرأسية بين الشكل وصورته.

مثال 

أجد قاعدة الانسحاب التي تنقل النجمة في الشكل المجاور من الموقع A إلى الموقع B

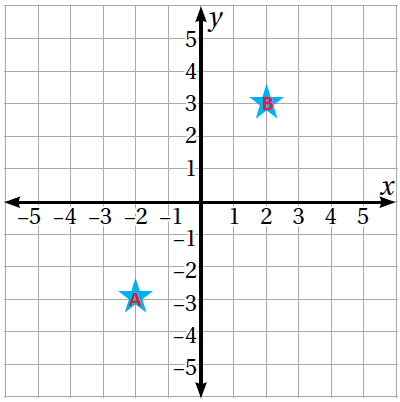
الحل : 

إحداثيا الموقع A هما (3- ، 2-) وإحداثيا الموقع B هما (3 ، 2) 

ألاحظ أنّ المسافة الأفقية بين الموقع A والموقع B هي 4 وحدات في اتجاه اليمين (الإشارة موجبة) و 6 وحدات إلى الأعلى (الإشارة موجبة) ، إذن

قاعدة الانسحاب هي : $(x , y) \to (x + 4 , y + 6)$