التمثيل الرياضي للموجات
التهيئة
|
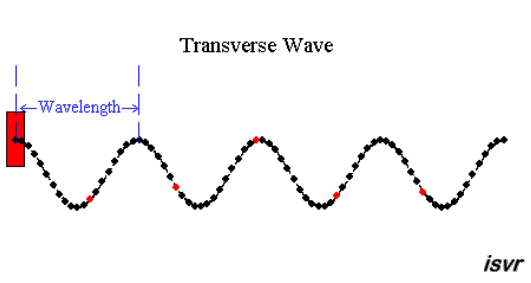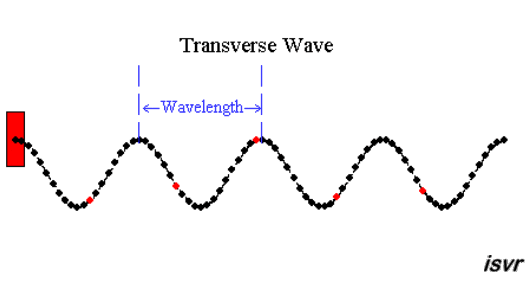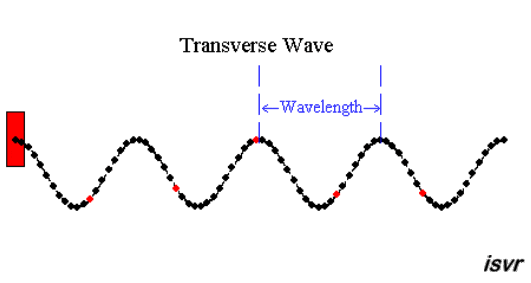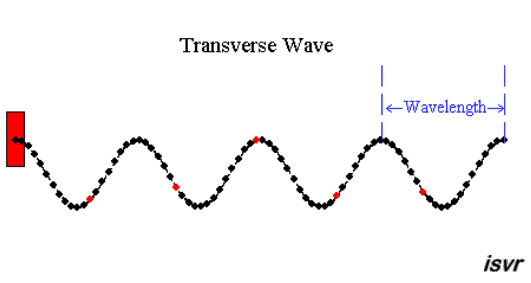
تنقـل الموجـات الطاقـة، وتختلف فـي صفاتهـا نتيجـة اختـلاف مصادرها.,تقسم الموجات حسب طبيعتها وحاجته لوسط معين إلى انتشاره إلى نوعين: - موجات ميكانيكية: وتمتاز بحاجتها لوسط مادي لانتقالها حيث تنتقل على شكل اضراب في الوسط. تقسم الموجات الميكانيكية إلى نوعين: 1- موجات مستعرضة Transvers Waves: حيث تهتز دقايق الوسط باتجاه متعامد مع انتشار الموجة ، كما في الشكل التالي، حيث الطول الموجي ( ) Wavelength : هو المسافة بين أي نقطتن متماثلتين ومتتاليتين. 2- موجات طولية Longitudinal Waves : وهي موجات تهتز دقائق الوسط بنفس اتجاه انتشار الموجات. لاحظ الشكل التالي:
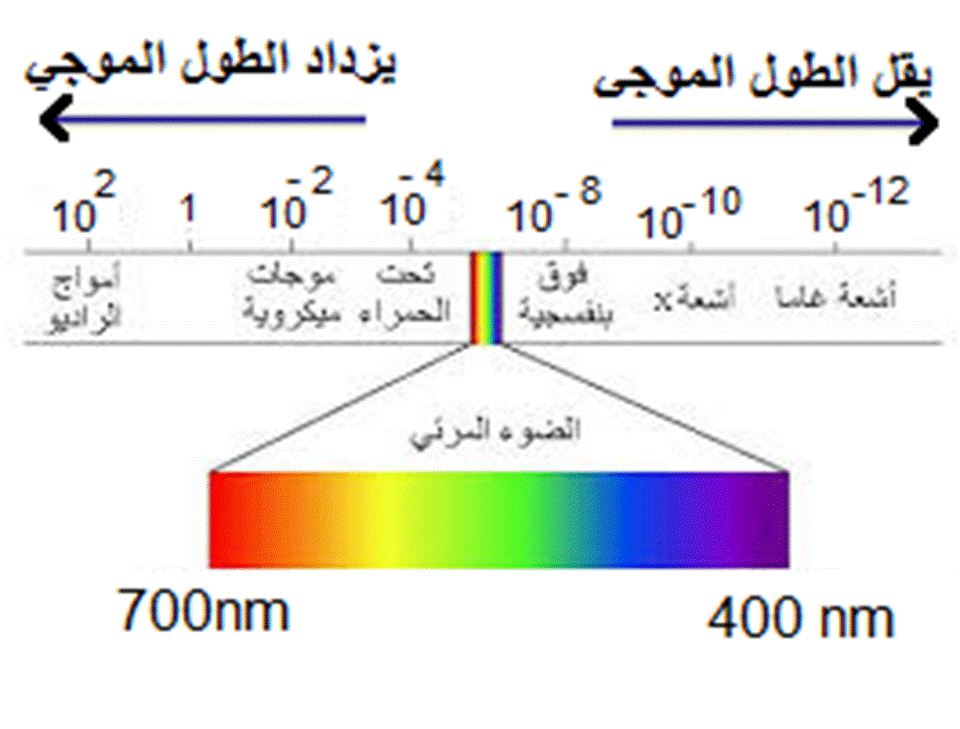
- موجات كهرومغناطيسية: موجات إشعاعية تضم أنواع مختلفة من الأشعة المرئية (ألوان الطيف السبعة. وإشعاع غير مرئي (الأشعة تحت الحمراء، والأشعة السينية وأشعة الراديو وأشعة جاما. وتشكل الموجات الكهرمغناطيسية ما يعرف بالطيف الكهرمغناطيسي الذي يتميز بما يأتي: 1- يتكون من مجالين كهلابائي ومغناطيسي ويتذبذب كل منهما على الآخر بشكل متعامد. 2- تلاحظ من الشكل في الأعلى أن موجات الطيف الكهرومغناطيسي هي موجات مستعرضة. 3- تنتقل جميع الموجات (الأطياف) الكهرومغناطيسية في الفراغ بسرعة () مهما كان ترددها. 4- لها طبيعة مزدوجة ( موجية وجسيمية)، أي يسلك هذا الطيف سلوك الموجات ويظهر في ظواهر بصفات جسيمية( مادية) ويتكون من حزم من الطاقة ( كمة) أي من وحدات أساسية من الطاقة كل كمة واحدة تسمى فوتون. الشكل. الطيف الكهرومغناطيسي. |
|||
|
وصف الموجات: - يتم وصف الموجات من خلال الطول الموجي()والسعة ( A ) والتردد (f ) والزمن الدوري (T) والسرعة ( v ) وتعطى سرعة جميع الموجات بدلالة الطول الموجي والتردد كما يلي:
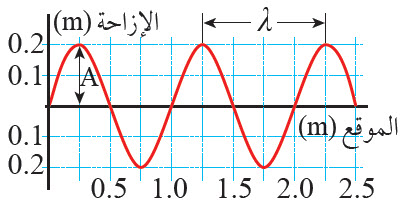
- يمكن تمثيل الحركة الموجية بيانا بطريقتين؛ الطريقة الأولى منحنی الإزاحة - الموقع)، والطريقة الثانية منحنى (الإزاحة - الزمن). منحنى (الإزاحة – الموقع: Displacement-position Graph) يصف هذا المنحنى البياني إزاحة جسيمات الوسط عن نقطة الاتزان عند مرور الموجة فيه، فالمنحنى يشبه صورة ثابتة (Snapshot)بين الموجة في لحظة زمنية معينة؛ أي عند تثبيت الزمن. كما يظهر في الشكل، إذ يمثل التدريج على محور (x) مواقع دقائق الوسط المهتزة وبعدها عن مصدر الموجة، ويمثل التدريج على محور (y) الإزاحة لدقائق الوسط عن نقطة الاتزان إلى أعلى وأسفل. ويظهر في هذا التمثيل البياني كل من الطول الموجي، والسعة.
|
|||
|
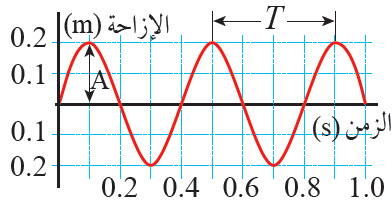
منحنی (الإزاحة – الزمن: Displacement-time Graph) يصف هذا المنحني البياني شكل الموجة بالنسبة إلى الزمن؛ إذ يصف الإزاحة الرأسية للجسيم واحد من جسيمات الوسط عننقطة اتزانه، وكيف يتغير موقع هذا الجسيم مع مرور الزمن. دون أن ننظر إلى جسيمات أخرى من الوسط، كما يبين الشكل.ألاحظ أن النقاط التي تتساوى في إزاحتها على المنحني، لا تعود الجسيمات مختلفة، بل تمثل مواقع جسيم واحد من الوسط عندلحظات زمنية دورية مختلفة؛ فالجسيم الواحد يصل إلى أعلى موقع، ثم ينخفض إلى أسفل موقع، ثم يعود إلى موقع اتزانه خلال دورة واحدة. وألاحظ على الشكل تلك الدورة ممثلة بالزمن الدوري للموجة، كما ألاحظ سعة الموجة ممثلة بأقصى إزاحة رأسية للجسيم نفسه. |
|||
 |
|||
|
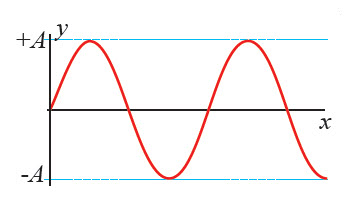
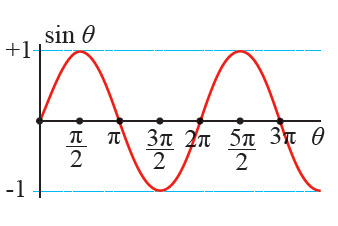
اقتران الموجة Wave Function إلى خصائص أخرى للموجات، والتعامل معالحركة الموجية بشكل أكثر دقة؛ لا بد من استخدام المعادلات الرياضية، والنظر إلى الموجة على أنها علاقة رياضية بين عدد من المتغيرات. وقد وجد تشابه بين منحنى الموجة ومنحنيات الاقترانات المثلثية؛ جيب الزاوية وجيب تمام الزاوية، ويمكن وصف الموجة عندما يتفق تمثيلها البياني مع اقتران الجيب بأنها موجة جيبية. عندما أثبت حبلا من أحد طرفيه وأشده قليلا، ثم أحرك طرفه الآخر حركة توافقية بسيطة، تنتشر فيه سلسلة من الموجات المستعرضة، فتحدث إزاحة لكل جزء من أجزاء الحبل إلى الأعلى والأسفل، أي إن الإزاحة بالنسبة إلى موقع الاتزان تتخذ قيما سالبة وأخرى موجبة، ويكون التمثيل البياني للموجة مشابها لأحد الاقترانات المثلثية وهو الاقتران الجيبي، الذي يصف العلاقةبين الزاوية (θ) وجيبها (sinθ)، كما جرى في وصف الحركة التوافقية البسيطة. وتسمى الزاوية (θ) زاوية الطور وهي تحدد شكل منحنى العلاقة الجيبية الناتج عن الاقتران: |
ألاحظ التشابه بين التمثيل البياني لانتشار موجة مستعرضة في حبل مشدود، والاقتران الجيبي للزاوية (θ). |
||
|
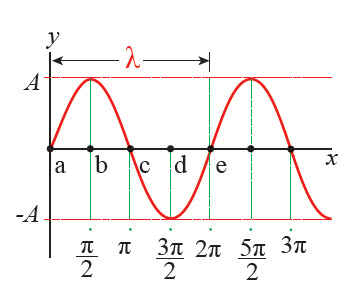
يصف اقتران الموجة التغير في موقع أي جسيم بالنسبة إلى متغيرين، هما؛ ُبعد الجسيم عن نقطة الأصل (x)، والزمن (t) مقاسًا من بداية الحركة الموجية، بافتراض أن الموجات جميعها متساوية في الطور، أي إنها تبدأ الاهتزاز من زاوية طور (θ = 0)، بإزاحة رأسية (y = 0). والموجات في حقيقة الأمر قد تختلف في الطور. لذا يمكنني إضافة ثابت الطور إلى اقتران الموجة، ليصبح على الصورة العامة الآتية: فتصبح زاوية الطور: θ = kx - ωt + ϕ إذ يشير الرمز (A) إلى سعة الموجة، ويمثل المقدار (kx) زاوية الطور للموجة، ويشير الرمز (k) إلى مقدار ثابت يسمى الرقم الموجي( k )،ويعرف بالعلاقة: باستخدام الرقم الموجي؛ يمكن حساب زاوية الطور التي تقابل أي موقع (x) عند الزمن 0 وثابت الطور 0 كما يأتي: فمثلًا في الشكل التالي عند الموقع (b) () تقابلها زاوية الطور:
ومنها نجد أن الإزاحة الرأسية عند النقطة (b) أعوض زاوية الطور: y(xb,0) = A sin () = A وكذلك لإيجاد الإزاحة الرأسية عند الموقع (a)؛ أعوض الموقع (xa = 0) في الاقتران الجيبي، فأحصل على: y(xa,0) = A sin (0) = 0 أما الموقع (c) فإنه يبعد عن نقطة الأصل بمقدار نصف طول موجي( ) فتكون زاوية الطور:
أي تكون الإزاحة الرأسية صفرًا، تقابله زاوية طور مقدارها ().ويمكن التحقق من ذلك بملاحظة الشكل. |
|||
|
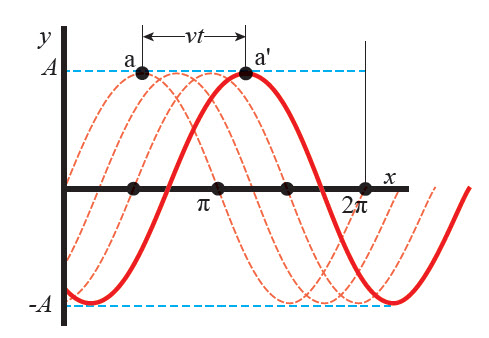
الإزاحة بدلالة الموقع والزمن ألاحظ أن الإزاحات الرأسية عند مواقع النقاط (…, a, b, c) رصدت في لحظة زمنية واحدة في بداية الحركة، عندما (t = 0). لكن الموجة تتقدم خلال زمن (t) نحو اليمين بسرعة (v) فتقطع كل نقطة على الموجة مسافة مقدارها (vt) نحو اليمين، كما يبين الشكل ألاحظ أن الإزاحة الرأسية للنقطة (a) عند الموقع (x) هي الإزاحة الرأسية نفسها للنقطة (a) عند الموقع (x - vt). وبشكل عام فإن الاقتران الموجي الذي يصف اعتماد حركة الموجة على كل من الموقع والزمن يعطى بالعلاقة: |
 |
مثال 1: تنتشر موجة جيبية افقياً في حبل مشدود باتجاه اليمين ( x + ) سعتها () وطولها الموجي ( )
وترددها ( )بناءاً على الشكل التالي أجد ما يأتي:
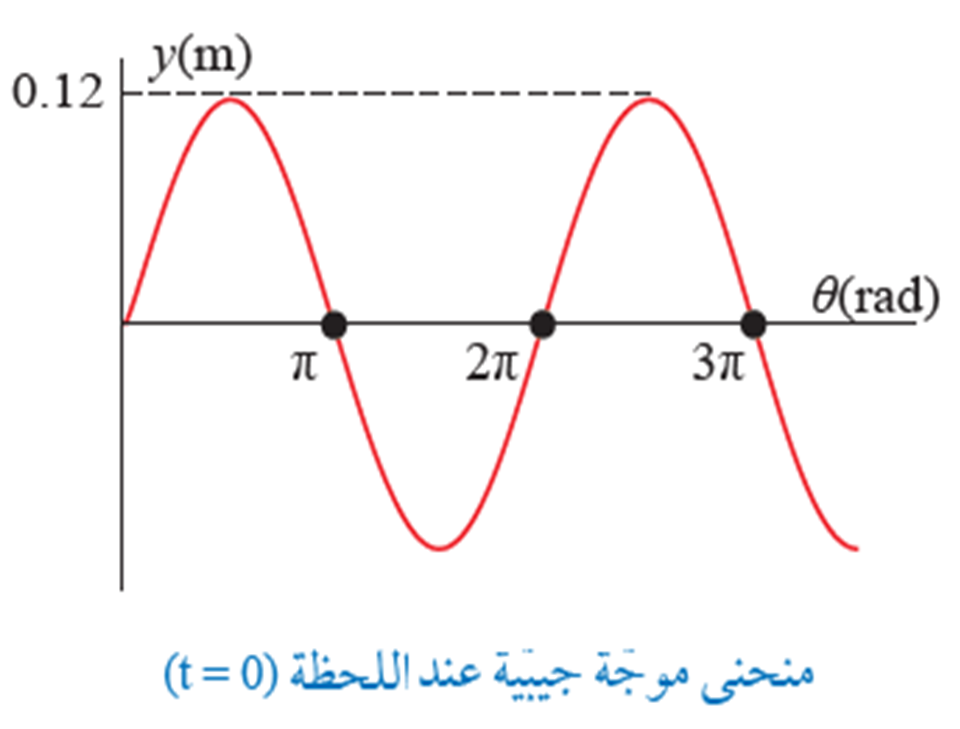
أ- مقدار الرقم الموجي( k ):
ب- أكتب اقتران الموجة عند اللحظة ( t=0 ).
جـ- الإزاحة الرأسية ( y ) للحبل عند الموقع ( ) واللحظة ( t=0 ).
الحل: أ- الرقم الموجي ( k ) :
ب- اقتران الموجة: لدينا سعة الموجة ( )
فيكون اقنران الموجة:
جـ- الإزاحة الراسية:
مثال 2: تنتشر موجة جيبية أفقياً في حبل مشدود بانجاه ( x +) وتوصف بالاقتران الآتي:
حيث تقاس ( x,y ) بوحدة المتر وتقاس (t) بوحدة ثانية، أجد مايلي:
أ- السعة ، التردد الزاوي الرقم الموجي.
ب- الطول الموجي ، سرعة الموجة.
جـ- الإزاحة الرأسية لجزء من الحبل يبعد عن نقطة الأصل ( ) عند اللحظة ( )
الحل: أ- بمقارنة الاقتران المعطى مع الاقتران العام للازاحة الرأسيى:
نجد : ,
ب- الطول الموجي( ) :
سرعة الموجة( ):
جـ- الإزاحة الرأسية:
ثابت الطور
ناقشنا حتى الآن إقتران موجة يصف التغير في الموقع ( y ) بالنسبة لمتغيرين ( x ) بعد الجسيم عن نقطة الأصل والزمن (t )
عند بداية الحركة ( )تكون ( ) وزاوية الطور ( ) وبعد فترة زمنية (t ) تكون زاوية الطور ( ).
جميع الموجات التي تتحرك بهذه الكيفية تكون متساوية في الطور، لكن لو كان هناك موجة مختلفة في الطور عند ( t=0 ) أي لحظة بداية الحركة،
عندها ستكون زاوية الطور ( ) حيث ( ) يسمى ثابت الطور. ويصبح لدينا الصورة العامة لاقتران تغير الموقع:
اختلاف الطور :
يمثل الشكل التالي منحنى الإزاحة - زاويةالطور، ويوجد مجموعة من النقاط على المنحنى.
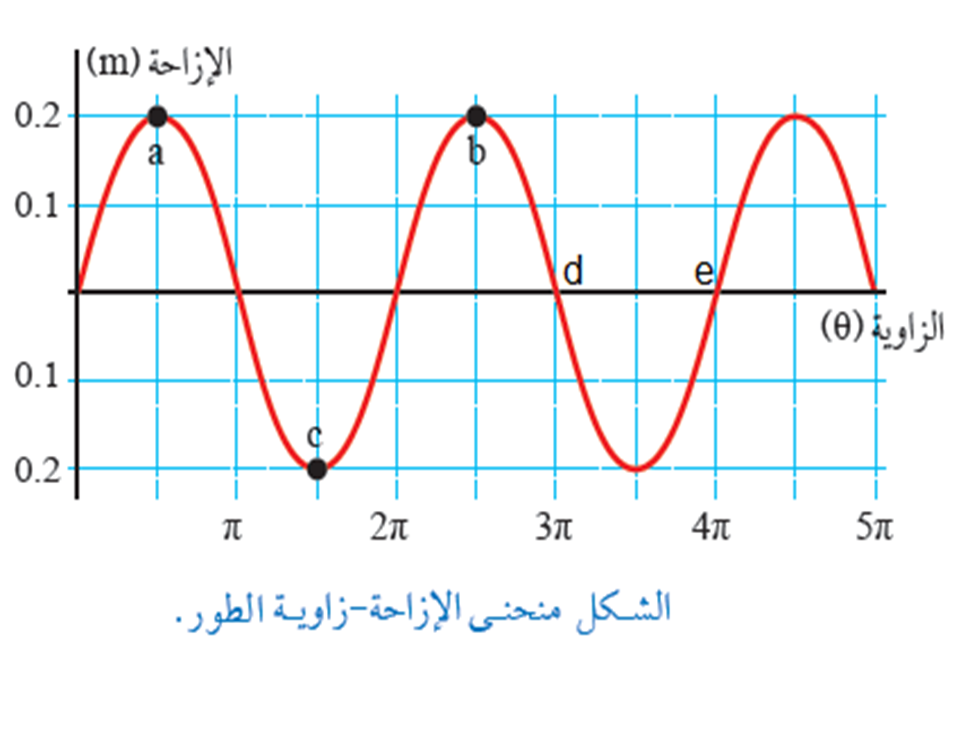
من الشكل نلاحط أن النقطة ( b ) سبقت كلاً من النقطتين ( a , c )يمكن والنقطة ( e ) سبقت جميع النفاط الواردة
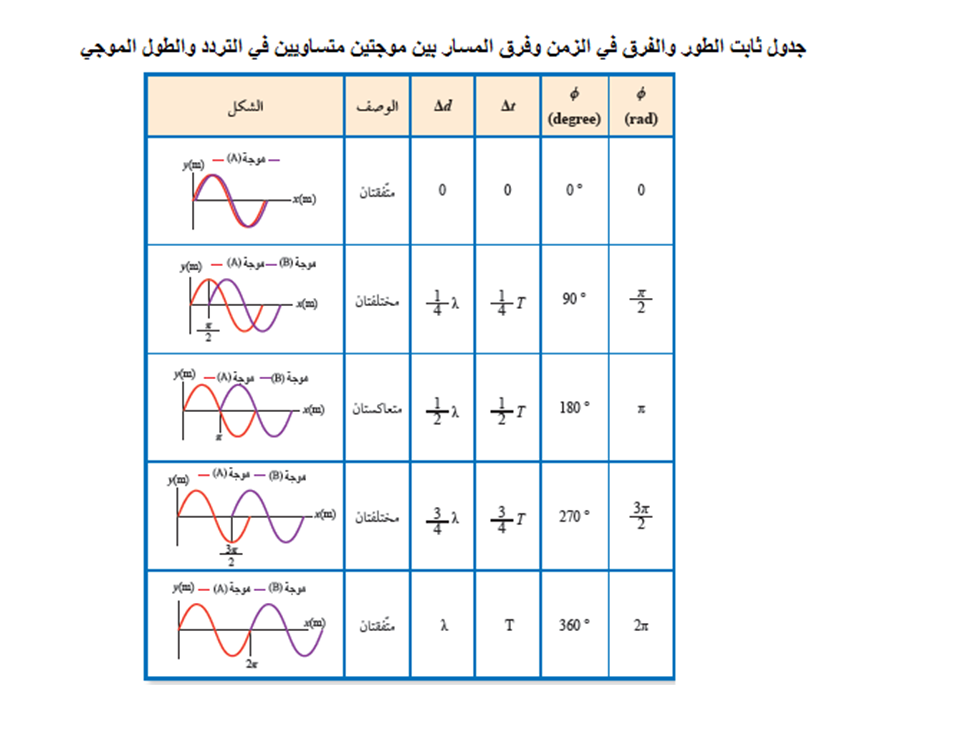
ولكل نقطة زاوية طور تختلف عن الأخرى، كما في الجدول التالي:
| النقطة | a | b | c | d | e |
| الطور |
يمكن حساب اختلاف الطور بين أي نقطتين، فمثلاً الفرق في زاوية الطور بين النقطتين ( a ) و ( b ):
أي أن النقطة (b ) تسبق النقطة (a )بمسافة تساوي طول موجي واحد أو بمقدار
زمن دوري واحد( T ).
و اختلاف زاوية الطور بين النقطتين (d ) و (e ) حيث يمثلان نقاط تقاطع المنحنى مع( ) الأفقي:
أي أن النقطة ( e ) تسبق النقطة ( d ) بمسافة تعادل نصف طول موجي
أو بزمن يساوي نصف زمن دورى، والنقطتان متعاكستان في إتجاه الإزاحة وهكذا يمكن حساب اختلاف الطور
إما عن طريق زاوية الطور أوبدلالة الطول الموجي أو بدلالة الفارق الزمني بالنسبة للزمن الدوري.
|
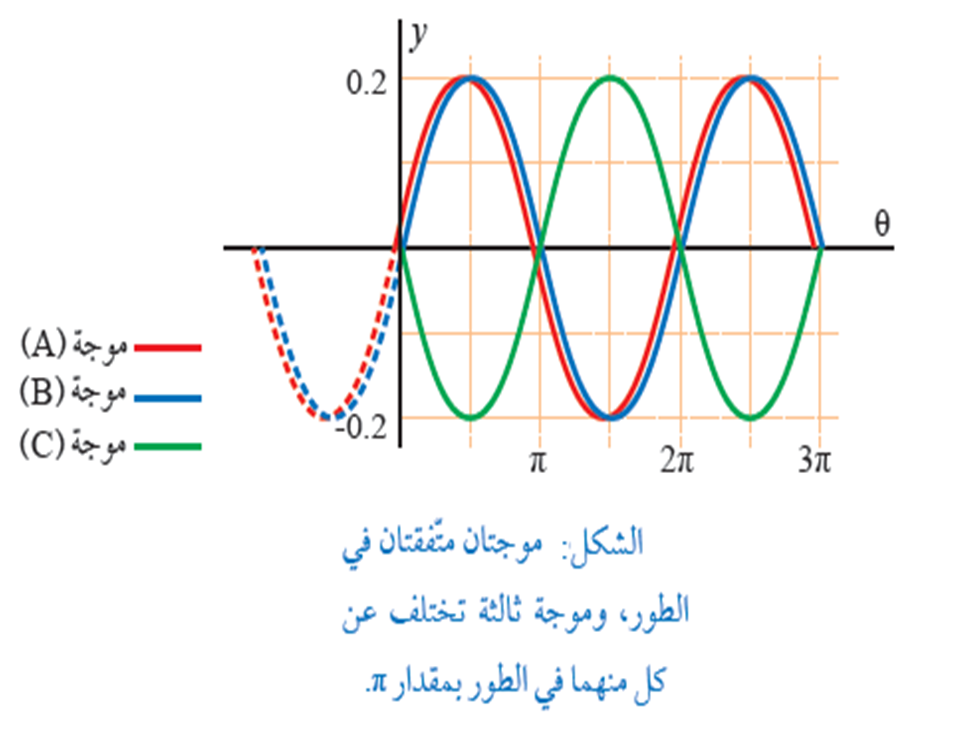
يمثل الشكل المجاور موجتين ( A, B )متفقتين في الطور حيث اختلاف زاوية الطور بينهما ( ) كذلك ينطبق الاتفاق في الطور عندما يكون الاختلاف في زاوية الطور: حيث n: عدد صحيح. بينما من الشكل نلاحظ أن الموجتين (A,C ) مختلفتان في الطور بمقدار . كذلك الموجتان ( B, C ) مختلفتان في الطور بمقدار .
|
 |
|
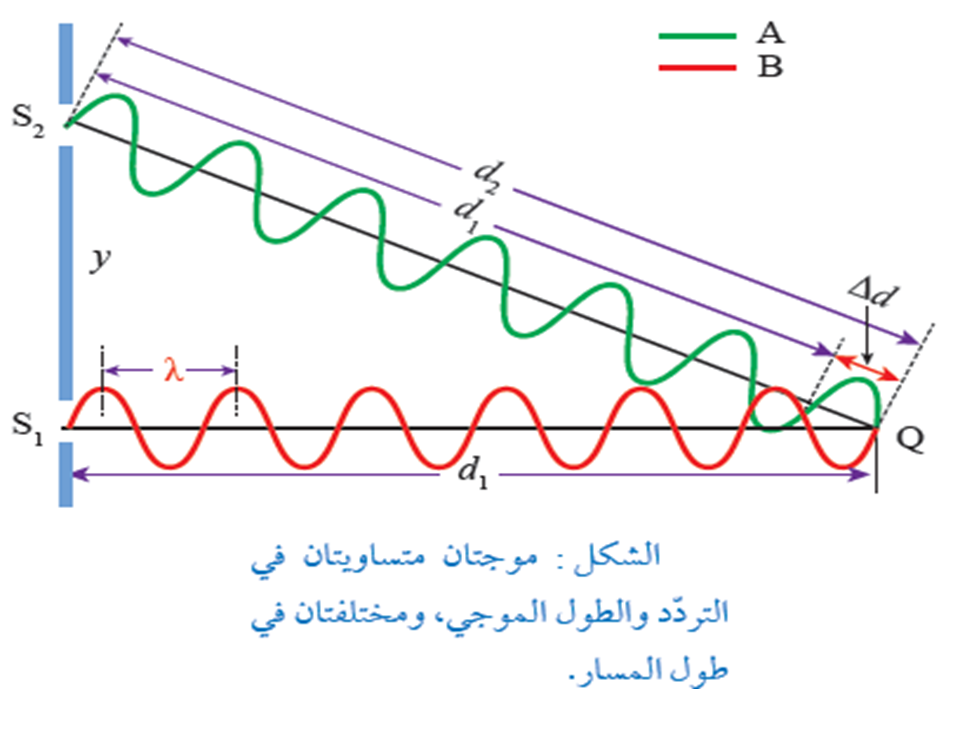
يبين الشكل المجاور موجتين ( A, B ) متساويتان في السعة والتردد وصادرتين من مصدرين ( ). ونلاحظ أن لهما زاوية الطور نفسها عند المصدرين، ويصبحان مختلفتان في الطور عندما يصلا النقطة(Q). من الشكل نلاحظ أن: المسار ( ) والمسار ( )بالتالي يكون فرق المسار بين الموجتين لحظة الوصول إلى النقطة( Q ) يكون: , وفرق المسار هذا بين الموجتين يعادل فرق طور ( )
|
 |
مثال 3: تنتشر موجة جيبية أفقياً في حبل مشدود باتجاه اليمين ( ( x + ) ، وتوصف بما يلي: سعتها ( ) وزمنها الدوري ( )
وسرعتها ( ) وثابت الطور ( ). أجد ما يأتي:
أ- أكتب الاقتران الموجي.
ب- احسب الإزاحة الرأسية عند ( )
الحل: أ- لكتابة الاقتران نحتاج ( ) لذلك يجب ايجاد كل من ( )
بالتالي يكون الاقتران الموجي:
ب- مقدار الإزاحة الرأسية:
|
مثال 4: موجتان ( A,B ) الطول الموجي لكل منهما ( ) تنتشران في الوسط نفسه، والشكل المجاور يبن منحنى ( الإزاحة - الزمن ) للموجتين معاً، بناءاً على الشكل، أجد ما يأتي: أ- الزمن الدوري والتردد لكل من الموجتين( A,B ) ب- الفارق الزمني الذي تأخرت به إحدى الموجتين عن الأخرى. جـ- الفرق في زاوية الطور. د- فرق المسار بين الموجتين.
|
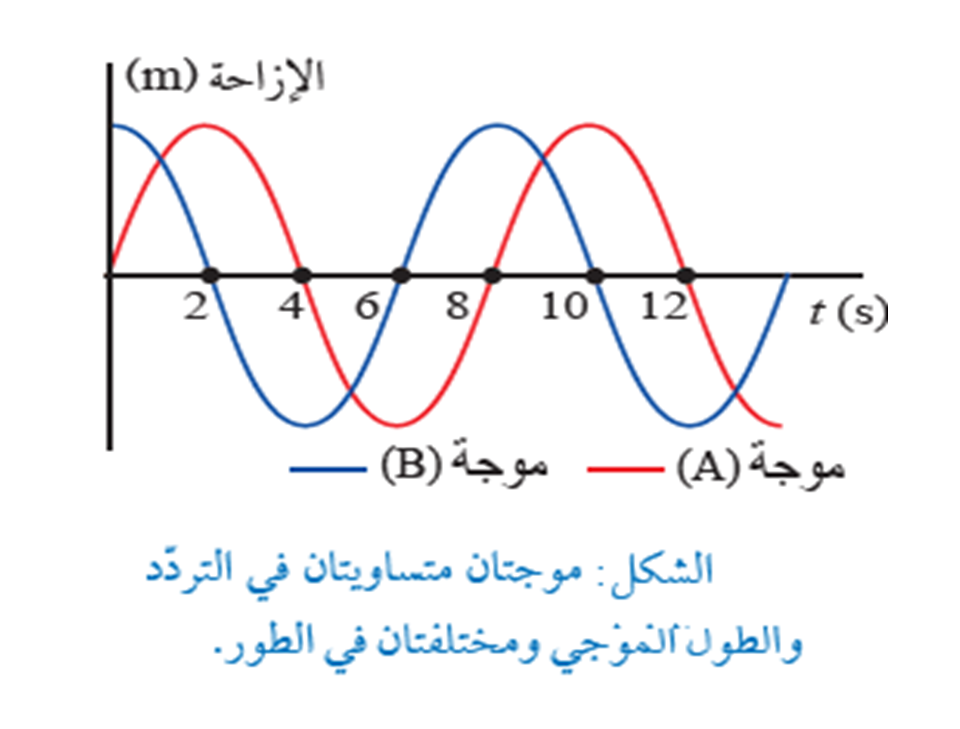 |
الحل: أ- من الشكل
ب- من الشكل نلاحظ أن الموجة (ِ A) تأخرت في حركتها عن الموجة ( B ) بمقدار ( ) وربع الموجة يعادل ثانيتين.
أي أن الموجة ( B ) بدأت حركتها قبل الموجة ( A ) بثانيتين، أي:
جـ - الفرق في زاوية الطور:
د- فرق المسار: