الفيزياء فصل ثاني

التمثيل الرياضي للموجات

تنقـل الموجـات الطاقـة، وتختلف فـي صفاتهـا نتيجـة اختـلاف مصادرها.,تقسم  الموجات حسب طبيعتها

وحاجته لوسط معين إلى انتشاره إلى نوعين:

   - موجات ميكانيكية:  وتمتاز بحاجتها إلى وسط مادي لانتقالها حيث تنتقل على شكل اضراب في الوسط.

تقسم الموجات الميكانيكية إلى نوعين:

- موجات مستعرضة: حيث تهتز دقائق الوسط باتجاه متعامد مع انتشار الموجة.

- موجات طولية: حيث تهتز دقائق الوسط بنفس اتجاه انتشار الموجات.

   - موجات كهرومغناطيسية: موجات إشعاعية تضم أنواع مختلفة  من الأشعة المرئية (ألوان الطيف السبعة).

    وإشعاع غير مرئي (الأشعة تحت الحمراء، والأشعة السينية وأشعة الراديو وأشعة جاما) يتميز بما يأتي:

• يتكون من مجالين كهلابائي  ومغناطيسي ويتذبذ كل منهما على الآخربشكل متعامد.
• تلاحظ من  الشكل في الأعلى أن  موجات الطيف الكهرومغناطيسي  هي  موجات مستعرضة.
• تنتقل جميع الموجات ( الأطياف )  الكهرومغناطيسية في الفراغ بسرعة (10⁸m/s× 3) مهما كان ترددها
• لها طبيعة مزدوجة ( موجية  وجسيمية)، أي يسلك هذا الطيف سلوك الموجات ويظهر في ظواهر بصفات جسيمية (مادية)

       ويتكون من حزم من الطاقة (كمه) أي من وحدات أساسية من الطاقة كل كمة واحدة تسمى فوتون.

 وصف الموجات 

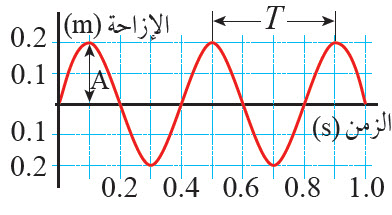
توصف الموجات من خلال الطول الموجي (l) والسعة (A) والتردد (ƒ) والزمن الدوري (T) والسرعة (v)

وتعطى سرعة  جميع الموجات  بدلالة الطول الموجي والتردد كما يلي:    l ×  ƒ= v

 يمكن تمثيل الحركة الموجية بيانيًا بطريقتين؛ الطريقة الأولى (منحنی الإزاحة - الموقع)، والطريقة الثانية منحنى (الإزاحة - الزمن).

      

اقتران الموجة
يصف اقتران الموجة التغير في موقع أي جسيم بالنسبة إلى متغيرين، هما؛ ُبعد الجسيم عن نقطة الأصل(x)،

والزمن (t) مقاسًا من بداية الحركة الموجية، بافتراض أن الموجات جميعها متساوية في الطور، أي إنها تبدأ الاهتزاز من زاوية طور

 (θ = 0)، بإزاحة رأسية (y = 0). والموجات في حقيقة الأمر قد تختلف في الطور، لذا يمكن إضافة ثابت الطور إلى اقتران الموجة،

 ليصبح على الصورة العامة الآتية:
      y = A sin (kx - ωt + ϕ)                                     

فتصبح زاوية الطور: θ = kx - ωt + ϕ

إذ يشير الرمز (A) إلى سعة الموجة، ويمثل المقدار (kx - $\omega$t +$\varphi$ ) زاوية الطور للموجة، ويشير الرمز (k) إلى مقدار

ثابت يسمى الرقم الموجي ( k ). والزاوية ($\varphi$ ) ثابت الطور.     

 الإزاحة بدلالة الموقع والزمن

الاقتران الموجي الذي يصف اعتماد حركة الموجة على كل من الموقع  والزمن يعطى  بالعلاقة:

                                         y(x, t) = A sin(kx - ωt)                  

اختلاف الطور

  - عند مقارنة موجتين متساويتين في التردد والسعة والطول الموجي؛ فإن زاوية الطور مهمة في هذه المقارنة، فعندما تبدأ الموجتان الحركة في اللحظة نفسها،

     وتكون الإزاحة متساوية( مقداراً واتجاها) عند الزوايا جميعها لكل من الموجتين؛ يمكن القول إن الموجتين متفقتان في الطور.

 - ينطبق الاتفاق في الطور أيضا على موجتين تبدأ إحداهما بعد بداية الأخرى بزاوية طور قياسها  ( 2π )، أو مضاعفات هذا القياس.

- يمكن أن يكون الاختلاف في الطور ناتج عن الفرق بين المسافة التي قطعتها موجتين .

- يمكن حساب اختلاف الطور إما عن طريق زاوية  الطور أو بدلالة  الطول الموجي أو بدلالة  الفارق الزمني بالنسبة للزمن الدوري.