حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 10
أُعَبِّرُ عنْ كلٍّ مِنَ المجموعاتِ الآتيةِ مُستعملًا طريقةَ سردِ العناصرِ، وطريقةَ الصِّفةِ المُمَيِّزَةِ:
a) مجموعةُ الأعدادِ الكُلية التي تقلّ عن 8
b) مجموعة مُضاعفات العددِ 3 التي تقل عن 18
c) مجموعة حلِّ المُعادلة 0 = 3x – 2
الحل :
a) مجموعةُ الأعدادِ الكُلية التي تقلّ عن 8
طريقة سردِ العناصرِ : { 7 , 6 , 5 , 4 , 3 , 2 , 1 , 0} = A
طريقةُ الصِّفة المُميّزة :
b) مجموعةُ مُضاعفاتِ العددِ 3 الَّتي تقلُّ عَنْ 18
طريقة سرد العناصر : { 15 , 12 , 9 , 6 , 3} = B
طريقةُ الصِّفة المُميّزة :
c) مجموعة حلِّ المُعادلة 0 = 3x – 2
أحل المعادلة أولًا :
طريقة سرد العناصر : { } = C
طريقةُ الصِّفة المُميّزة :
أتحقق من فهمي صفحة 11
أكتبُ كلَّ مجموعة ممّا يأتي بطريقة سرد العناصر، ثمَّ أُحَدِّدُ ما إذا كانت خالية، أمْ مفردة، أمْ منتهية، أم غير منتهية:
a) P = { x | x > 10, x ∈ W } b) O = { x | x = 2k, k ∈ Z }
c) D = { x | 0.5x + 10 = 0} d) D = { x | x < 0, x ∈ W }
e)
الحل :
a) P = { x | x > 10, x ∈ W }
تمثِّلُ P مجموعةَ الأعدادِ الكلية التي تزيد عن 10 ، وَتُكتَبُ بطريقة سرد العناصر، كما يأتي:
P = {11, 12 , 13 ,…} ، وهي مجموعةُ غيرُ منتهية.
b) O = { x | x = 2k, k ∈ Z }
تمثِّلُ O مجموعة الأعدادِ الزوجية ، وتُكتب بطريقة سرد العناصر، كما يأتي:
O = {…, -6, -4, -2, 0 , 2, 4, 6, …} ، وهي مجموعة غير منتهية.
c) D = { x | 0.5x + 10 = 0}
تمثِّل D مجموعة حلِّ المُعادلة 0 = 0.5x + 10 ، وتُكتب بطريقة سرد العناصر، كما يأتي:
D = {-20} ، وهي مجموعة مُفردة.
d) D = { x | x < 0, x ∈ W }
تمثِّلُ D مجموعة الأعداد الصحيحة السالبة ، وتُكتب بطريقة سرد العناصر كما يأتي:
D = { …, -3 , -2 , -1 } ، وهي مجموعة غير منتهية.
تمثِّل T مجموعة مربعات الأعداد الكلية التي تقل عن 5 ، وَتُكتَبُ بطريقةِ سردِ العناصِرِ، كما يأتي:
T = {0 , 1 , 4 , 9 , 16 } ، وهي مجموعة منتهية.
أتحقق من فهمي صفحة 12
أكتب مجموعة حلِّ كلِّ مُتباينة ممّا يأتي باستعمال الصِّفة المُميزة:
a) 2x + 10 ≤ 14 b) 3x + 3 < 4x - 5
الحل :
a) 2x + 10 ≤ 14
| المُتباينةُ الأصليَّةُ | |
| بطرح 10 من طرفي المتباينة | |
| بِقِسمَةِ طرفَيِ المُتباينةِ على 2 | |
| بالتبسيطِ |
إذن ، مجموعةُ الحلِّ هِيَ
b) 3x + 3 < 4x - 5
| المُتباينةُ الأصليَّةُ | |
| بطرح 3 من طرفي المتباينة | |
| بِطرح 4x من طرفَيِ المُتباينةِ | |
| بِضرب طرفَيِ المُتباينة قي 1 - ، وتغييرِ اتّجاهِ رمزِ المتباينة | |
| بالتبسيطِ |
إذن ، مجموعةُ الحلِّ هِيَ
أتحقق من فهمي صفحة 15
أكتبُ كلَّ مُتباينةٍ ممّا يأتي باستعمالِ رمزِ الفترةِ، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
a) x ≤ -2 b) x ≥10 c) x < 8 d) x > -7
الحل :
a) x ≤ -2
رمزُ الفترةِ :
التمثيلُ على خطِّ الأعدادِ:
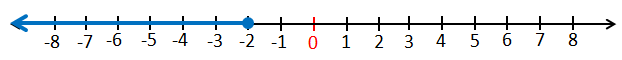
b) x ≥10
رمزُ الفترةِ :
التمثيلُ على خطِّ الأعدادِ:

c) x < 8
رمزُ الفترةِ :
التمثيلُ على خطِّ الأعدادِ:
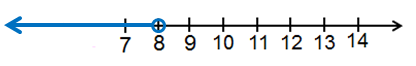
d) x > -7
رمزُ الفترةِ :
التمثيلُ على خطِّ الأعدادِ:

أسئلة أتدرب وأحل المسائل
أُعَبِّرُ عَنْ كلٍّ مِنَ المجموعاتِ الآتيةِ مستعملًا طريقةَ سردِ العناصِرِ، وَطريقةَ الصِّفةِ المُمَيِّزَةِ:
1) مجموعةُ الأعدادِ الكُليَّةِ الَّتي تزيدُ على أوْ تُساوي 20 2) مجموعةُ مُضاعفاتِ العددِ 4 الَّتي تقلُّ عَنْ 50
3) مجموعةُ الأعدادِ الفرديَّةِ الَّتي تزيدُ على أوْ تُساوي 11 4) مجموعةُ الأعدادِ الصَّحيحةِ الَّتي تقلُّ عَنْ 4-
5) مجموعةُ الأعدادِ الزوجيَّةِ الَّتي تقلُّ عَنْ أوْ تُساوي 100 6) مجموعةُ حلِّ المُعادلةِ 0 = 5x – 30
7) مجموعةُ مُضاعفاتِ العددِ 5 الَّتي تقلُّ عَنْ 4 8) مجموعةُ الأعدادِ الكُليَّةِ الَّتي تقعُ بينَ العددَيْنِ 1 وَ 15
الحل :
1) مجموعةُ الأعدادِ الكُليَّةِ الَّتي تزيدُ على أوْ تُساوي 20
طريقة سردِ العناصرِ : {... , 24 , 23 , 22 , 21 , 20} = A
طريقةُ الصِّفة المُميّزة :
2) مجموعةُ مُضاعفاتِ العددِ 4 الَّتي تقلُّ عَنْ 50
طريقة سردِ العناصرِ : { 48 ,44 , 40 ,36 ,32 ,28 ,24 ,24 , 20 , 16 , 12 , 8 , 4} = B
طريقةُ الصِّفة المُميّزة :
3) مجموعةُ الأعدادِ الفرديَّةِ الَّتي تزيدُ على أوْ تُساوي 11
طريقة سردِ العناصرِ : { ..., 19 , 17 , 15 , 13 , 11} = C
طريقةُ الصِّفة المُميّزة :
4) مجموعة الأعداد الصحيحة التي تقلّ عن 4-
طريقة سردِ العناصرِ : { 5- , 6- , 7- , 8- , ...} = D
طريقةُ الصِّفة المُميّزة :
5) مجموعةُ الأعدادِ الزوجيَّةِ الَّتي تقلُّ عَنْ أوْ تُساوي 100
طريقة سردِ العناصرِ : { 100 , 98 , 96 , 94 , ...} = E
طريقةُ الصِّفة المُميّزة :
6) مجموعةُ حلِّ المُعادلةِ 0 = 5x – 30
طريقة سردِ العناصرِ : {6} = F
طريقةُ الصِّفة المُميّزة :
7) مجموعةُ مُضاعفات العددِ 5 التي تقلُّ عن 4
طريقة سرد العناصر : { } = G
طريقةُ الصِّفة المُميّزة :
8) مجموعةُ الأعدادِ الكُليَّةِ الَّتي تقعُ بينَ العددَيْنِ 1 وَ 15
طريقة سردِ العناصرِ : = H
طريقةُ الصِّفة المُميّزة :
أكتبُ كلَّ مجموعةٍ ممّا يأتي بطريقةِ سردِ العناصِرِ، ثمَّ أُحَدِّدُ ما إذا كانتْ خاليةً، أمْ مفردةً، أمْ منتهيةً، أمْ غيرَ منتهيةٍ:
9) A = {x | x ∈ W, x ≤ 1} 10) B ={x | 3x + 1 = 0}
11) C = {x | x < 2, x ∈ Z } 12) D = {x | x2 = x, x ∈ Z }
13) E = {x | x = 6k, k ∈ W, x < 5} 14) T = {x | x = k3 , k ∈ W, x < 80}
الحل :
9) A = {x | x ∈ W, x ≤ 1}
تمثِّلُ A مجموعةَ الأعدادِ الكلية الَّتي تقل عن أو تساوي 1، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
ِA = {... , -2 , -1 , 0 , 1} ، وهي مجموعةُ غيرُ منتهيةٍ.
10) B ={x | 3x + 1 = 0}
تمثِّلُ B مجموعةَ حل المعادلة 3x + 1 = 0 ، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
، وهي مجموعةُ مُفردة.
11) C = {x | x < 2, x ∈ Z }
تمثِّلُ C مجموعةَ الأعدادِ الصحيحة الَّتي تقل عن 2 ، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
C = {...-2 , -1 , 0 , 1 } ، وهي مجموعةُ غيرُ منتهيةٍ.
12) D =
أحل المعادلة :
تمثِّلُ D مجموعةَ حل المعادلة ، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
D = {0 , 1} ، وهي مجموعةُ منتهيةٍ.
13) E = {x | x = 6k, k ∈ W, x < 5}
تمثِّلُ E مجموعةَ مضاعفات العدد 6 الَّتي تقل عن 5 ، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
، وهي مجموعةُ خالية.
14) T = {x | x = , k ∈ W, x < 80}
تمثِّلُ T مجموعةَ مُكعبات الأعداد الكلية التي تقل عن 80 ، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
T = {0 , 1 , 8 , 27 , 64} ، وهي مجموعةُ منتهيةٍ.
أكتبُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي باستعمالِ الصِّفةِ المُمَيِّزَةِ:
15) 7 + 6x < 19 16) 2(y + 2)-3y ≥ -1 17) 18x - 5 ≤ 3(6x -2)
الحل :
| إذن مجموعة حل المتباينة هي : |
15) 7 + 6x < 19 |
|
إذن مجموعة حل المتباينة هي :
|
16) 2(y + 2)-3y ≥ -1 |
|
عبارة خاطئة ، إذن مجموعة حل المتباينة
|
17) 18x - 5 ≤ 3(6x -2) |
أكتبُ كلَّ مُتباينةٍ ممّا يأتي باستعمالِ رمزِ الفترةِ، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
18) x < -7 19) x > 12 20) x ≤ 1 21) x ≥ -20
الحل :
18) x < -7
رمزُ الفترةِ :
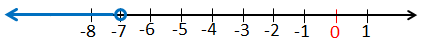
19) x > 12
رمز الفترة :
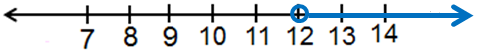
20) x ≤ 1
رمز الفترة :

21) x ≥ -20
رمز الفترة :

أكتبُ المُتباينةَ المُمَثَّلَةَ على خطِّ الأعدادِ في كلٍّ ممّا يأتي، ثمَّ أُعَبِّرُ عنها باستعمالِ رمزِ الفترةِ:

الحل :
22 ) المتباينة : ، التعبير باستخدام رمز الفترة :
23) المتباينة : ، التعبير باستخدام رمز الفترة :
مهاراتُ التفكيرِ العُليا
24) أكتشفُ الخطأَ: أعادَ أحمدُ كتابةَ الفترةِ [ 8- ,∞ -) باستعمالِ الصِّفةِ المُمَيِّزَةِ، كما هُوَ مُبَيَّنٌ جانبًا.
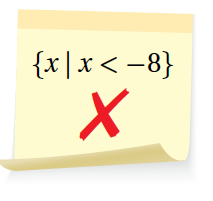
أُبَيِّنُ الخطأَ الَّذي وقعَ فيهِ أحمدُ، وَأُصَحِّحُهُ.
الحل :
الخطأ الذي وقع فيه أحمد بوضع رمز المتباينة بدون المساواة ؛ لأنّ رمز الفترة مغلق عند x = -8
والصحيح :
25) تَحَدٍّ: أكتبُ المجموعةَ باستعمالِ الصِّفةِ المُمَيِّزَةِ.
الحل :
26) أكتشفُ المُختَلِفَ: أيٌّ ممّا يأتي مختلفٌ؟ أبرّرُ إجابتي:
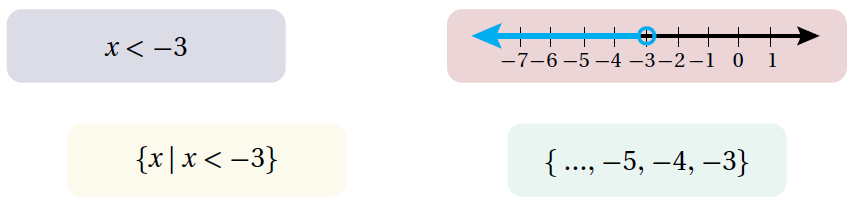
الحل :
المختلف : لأنها مجموعة تنتمي إلى مجموعة الأعداد الكلية W، بينما باقي المجموعات تنتمي إلى مجموعة الأعداد الحقيقية R.
أسئلة كتاب التمارين
أُعَبِّرُ عَنْ كُلٍّ مِنَ المجموعاتِ الآتيةِ، مُستعملً طريقةَ سردِ العناصرِ، وَطريقةَ الصِّفةِ المُمَيِّزَةِ:
1) مجموعةُ الأعدادِ الكُلِّيَّةِ الَّتي تقلُّ عَنْ 17 2) مجموعةُ مُضاعفاتِ العددِ 10 الَّتي تقلُّ عَنْ 12
3) مجموعةُ حلِّ المُعادلةِ : 4) مجموعةُ الأعدادِ الكُلِّيَّةِ الَّتي تزيدُ على 200
5) مجموعةُ الأعدادِ الصَّحيحةِ الَّتي تقلُّ عَنْ 6) مجموعةُ الأعدادِ الصَّحيحةِ السالبةِ.
الحل :
1) مجموعةُ الأعدادِ الكُلِّيَّةِ الَّتي تقلُّ عَنْ 17
طريقة سردِ العناصرِ : {16 , 15 , 14 ,13, 12 , 11 , 10 , 9 , 8 ,7 , 6 , 5 , 4 , 3 , 2 , 1 , 0} = A
طريقةُ الصِّفة المُميّزة :
2) مجموعةُ مُضاعفاتِ العددِ 10 الَّتي تقلُّ عَنْ 12
طريقة سردِ العناصرِ : {10}
طريقةُ الصِّفة المُميّزة :
3) مجموعةُ حلِّ المُعادلةِ :
طريقة سردِ العناصرِ : { 4-}
طريقةُ الصِّفة المُميّزة :
4) مجموعةُ الأعدادِ الكُلِّيَّةِ الَّتي تزيدُ على 200
طريقة سردِ العناصرِ : {... ، 204 ، 203 , 202 , 201}
طريقةُ الصِّفة المُميّزة :
5) مجموعةُ الأعدادِ الصَّحيحةِ الَّتي تقلُّ عَنْ
طريقة سردِ العناصرِ :
طريقةُ الصِّفة المُميّزة :
6) مجموعةُ الأعدادِ الصَّحيحةِ السالبةِ.
طريقة سردِ العناصرِ : { 1- ، 2- ، 3- , 4- , ... }
طريقةُ الصِّفة المُميّزة :
أكتبُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي باستعمالِ الصِّفة المُمَيِّزَةِ:
7) 6z - 15 > 4z + 11 8) 3y + 6 < 2y - 8 9)
10) 3(x - 2) ≥ 15 11) -5 ≤ 4x + 7 12) 5x - 7 > 3x + 4
الحل :
| مجموعة حل المتباينة هي : |
7) 6z - 15 > 4z + 11
|
| مجموعة حل المتباينة هي : |
8) 3y + 6 < 2y - 8 |
| مجموعة حل المتباينة هي : |
9)
|
| مجموعة حل المتباينة هي : |
10) 3(x - 2) ≥ 15
|
| مجموعة حل المتباينة هي : |
11) -5 ≤ 4x + 7 |
| مجموعة حل المتباينة هي : |
12) 5x - 7 > 3x + 4
|
أكتبُ كلَّ مجموعةٍ ممّا يأتي بطريقةِ سردِ العناصرِ، ثمَّ أُحَدِّدُ ما إذا كانتْ خاليةً، أمْ مفردةً، أمْ منتهيةً، أمْ غيرَ منتهيةٍ:
13) A = { x | x ∈ Z, x < 5} 14) B = { x | 5x - 1= 0}
15) C = { x | x < 7, x ∈ W} 16) D = { x | x = k-1, k ∈ W, k < 11}
17) E = { x | x = 8k, k ∈ W, x > 20} 18) T = { x | x = 2k, k ∈ Z, x > 10}
الحل :
13) A = { x | x ∈ Z, x < 5}
A = { … , -1 , 0 , 1 , 2 , 3 , 4 } ، وهي مجموعة غير منتهية.
14) B = { x | 5x - 1 = 0}
، وهي مجموعة مُفردة.
15) C = { x | x < 7, x ∈ W}
A = { 0 , 1 , 2 , 3 , 4 , 5 , 6 } ، وهي مجموعة منتهية.
16) D = { x | x = k - 1, k ∈ W, k < 11}
D = { 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 , 0 , -1} ، وهي مجموعة منتهية.
17) E = { x | x = 8k, k ∈ W, x > 20}
D = { 24 , 32 , 40 , 48 , ... } ، وهي مجموعة غير منتهية.
18) T = { x | x = 2k, k ∈ Z, x > 10}
T = { 12 , 14 , 16 , 18 , ... } ، وهي مجموعة غير منتهية.
أكتبُ المُتباينةَ الممثَّلَةَ على خطِّ الأعدادِ في كلٍّ ممّا يأتي، ثمَّ أُعَبِّرُ عنها باستعمالِ رمزِ الفترةِ:

الحل :
19) المتباينة : ،
20) المتباينة : ،
21) المتباينة : ،
22) المتباينة : ،
أكتبُ كلَّ مُتباينةٍ ممّا يأتي باستعمالِ رمزِ الفترةِ، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
23) x < 15 24) x > -5 25) x ≤ -10 26) x ≥ 30
الحل :
23) x < 15
التعبير برمز الفترة :
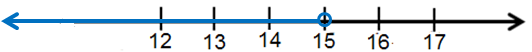
24) x > -5
التعبير برمز الفترة :

25) x ≤ -10
التعبير برمز الفترة :