العلوم

أستكشف : قياس السرعة على سطح منحدر 

الموادُّ والأدواتُ:لوحٌ خشبيٌّ طولُهُ ( 1m) وعرضُهُ( 10cm) (يمكنُ الاستبدالُ بهِ ما يتوافرُ في البيئةِ حولَنا، لكنْ لا بدَّ منْ قياسِ طولِهِ قبلَ التجربةِ)، وكرةٌ، وساعةُ توقيتٍ.
إرشاداتُ السلامةِ: أتجنّبُ اللَّعبَ بالكراتِ في الغرفةِ الصفّيّةِ؛ لأنَّ ذلكَ قدْ يتسبّبُ في ضررٍ بالغٍ.
خطواتُ العملِ:
1. أجرِّبُ: أضعُ طرفَ اللَّوحِ على ارتفاعِ ( 10cm).(يمكنُني رفعُهُ بالاستعانةِ بكتُبي). يجبُ أنْ يبقى الارتفاعُ ثابتًا طوالَ التجربةِ. ألصقُ قطعةَ شريطٍ لاصقٍ على بدايةِ اللَّوحِ لتشيرَ إلى خطِّ البدايةِ، ثمَّ ألصقُ قطعةً أُخرى لتشيرَ إلى خطِّ النهايةِ.
2. أتواصلُ: أطلبُ إلى زميلي الأوّلِ في المجموعةِ أنْ يضعَ الكرةَ عندَ نقطةِ البدايةِ، وإِلى زميلي الآخرِ أنْ يقيسَ الزمنَ بساعةِ التوقيتِ عندَما يسمعُني أقولُ "أبدا"، أوْ "توقَّفْ" لحظةَ بدايةِ الحركةِ ونهايتِها (أتأكَّدُ أنَّ الطولَ بينَ البدايةِ والنهايةِ 1m).
3 . ألاحظُ: أتركُ الكرةَ تتدحرجُ معَ تشغيلِ ساعةِ التوقيتِ. عندَما تصلُ الكرةُ إلى نقطةِ النهايةِ أوقفُ تشغيلَ الساعةِ، ثمَّ أُدوِّنُ الزمنَ في جدولٍ.
4. أسجِّلُ البياناتِ: لتقليلِ الخطأ في التجربةِ، يُفضَّلُ إعادةُ الخطوةِ السابقةِ ( 5) مراتٍ، وتدوينُ الزمنِ في كلِّ مرَّةٍ، ثمَّ حسابُ متوسِّطِ الزمنِ للمحاولاتِ جميعِها.
5. أقيسُ: أُضيفُ عمودًا جديدًا إلى الجدولِ، ثمَّ أحسبُ فيهِ ناتجَ قسمةِ المسافةِ بينَ نقطةِ البدايةِ والنهايةِ على الزمنِ.
6. أستنتجُ: أكتبُ النتيجةَ التي توصَّلْتُ إليها.
7. أتواصلُ: أتحدَّثُ إلى زملائي، وأصفُ لهُمُ الكميّةَ الفيزيائيّةَ التي نَتَجَتْ منْ قسمةِ المسافةِ على الزمنِ.
التفكيرُ النّاقدُ: لوِ استخدمتُ كرةً كتلَتُها أكبرُ، وكرّرتُ التجربةَ بحيثُ تقطعُ الكرةُ المسافةَ نفسَها؛ هل سيتغيَّرُ زمنُ الوصولِ؟

لا تعتمد السرعة على كتلة الجسم، فعندما تكون المسافة على المنحدر ثابتة، فإن سرعة الأجسام لا تتغير بتغير كتلها. أي أن زمن وصولها نفسه.

 

الحركةُ Motion

• نعيشُ في عالَمٍ متحرِّكٍ؛ فالرّياحُ تهبُّ والسياراتُ تسيرُ، والأطفالُ يقضونَ وقتًا ممتعًا في الركضِ. لذلكَ فإنّنا نحتاجُ إلى طريقةٍ منظّمةٍ لوصفِ حركةِ الأجسامِ.
• الحركةُ Motion تَغَيُّرٌ مستمرٌّ في موقعِ جسمٍ ما مقارنةً بأجسامٍ ثابتةٍ حولَهُ.
• الموقعُ Position فهوَ بُعْدُ الجسمِ عنْ نقطةٍ إسنادٍ (نقطةٍ مرجعيةٍ).
• لتحديدِ موقعِ الجسمِ، ينبغي تحديدُ نقطةٍ مرجعيّةٍ نستندُ إليها، تسمّى نقطةَ إسنادٍ Reference Point

                                      

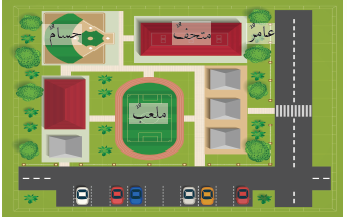
• عند دراسة الشكل أعلاه ، بعدَ تفرُّقِ الصديقينِ حسامٍ وعامرٍ في أثناءِ رحلةٍ مدرسيّةٍ إلى حدائقِ الملكِ عبدِاللهِ الثاني ابنِ الحسينِ،هاتفَ حسامٌ صديقَهُ عامرًا؛ ليسألَهُ عنْ مكانِهِ بدقَّةٍ. وقدْ تمكَّنَ كلٌّ منْهُما منْ تحديدِ مكانِهِ بالنسبةِ إلى مَعْلَمٍ ثابتٍ يُعَدُّ نقطةً مرجعيَّةً إليْهِ. فعامرٌ مثلاً يقفُ شرقَ المتحفِ، وحسامٌ شمالَ غربِ الملعبِ.

 

أتحقَّقُ: أُحدِّدُ موقع حسامٌ في ساحةِ المدرسةِ بالنسبةِ إلى ساريةِ العلَمِ.

تحديد موقع سارية العلم في المدرسة ومن ثم تحديد موقع حسام بالنسبة للسارية.

 

المسافةُ والإزاحةُ Distance and Displacement

• عندَما نريدُ وصفَ حركةِ جسمٍ ما يتحرَّكُ في خطٍّ مستقيمٍ فإنَّنا نحتاجُ إلى قياسِ المسافةِ التي يتحرَّكُها ، وإيجادِ الزّمنِ الذي يستغرقُهُ في قطعِ هذهِ المسافةَ. 
• تُعرَّفُ المسافةُ Distance بأنّها الطولُ الكلّيُّ للمسارِ الذي يسلُكُهُ الجسمُ في أثناءِ انتقالِهِ بينَ نقطتينِ. وتُقاسُ بوحدةِ المترِ (m)، أوْ مضاعفاتِها، مثلِ: الكيلو مترِ (km)، أوْ أجزاءٍ منْها، مثلِ: السنتيمترِ (cm)، والملّيمترِ (mm).
• تعدُّ المسافةُ كميّةً قياسيَّةً Scalar Quantity ؛ أيْ إنّهُ يكفي لتحديدِها معرفةُ مقدارِها فقطْ؛ فنقولُ: إنَّ المسافةَ بينَ محافظةِ عمّانَ والزرقاءِ ( 30 km) تقريبًا، ويُرمَزُ إلى المسافةِ بالرمزِ (S).
• قدْ يوجدُ أكثرُ منْ مسارٍ يصلُ بينَ نقطتينِ. ويُسمى أقصرُ مسارٍ مستقيمٍ يصلُ بينَ نقطةِ بدايةِ الحركةِ ونهايتِها الإزاحةَ Displacement
• تعتبر الإزاحة  كميَّةٌ متّجهةٌ  Vector Quantity ؛ أيْ إنَّهُ يلزمُ لتحديدِها معرفةُ مقدارِها واتّجاهِها معًا، ويُرمَزُ إلى الإزاحةِ بالرمزِ (Δx).
• يُكتَبُ الرمزُ(Δ) ويُقرَأُ (دلتا) للتعبيرِ عنِ الفرقِ بينَ الموقعِ النهائيِّ للجسمِ وموقعِهِ في البدايةِ منْ دونِ الاهتمامِ بالمسارِ الذي سلكَهُ الجسمُ بينَهُما.

 

الربط بالرياضيات 

تُعدُّ قمَّةُ إيفريستْ أعلى نقطةٍ على سطحِ الأرضِ؛ إذْ بلغَ ارتفاعُها عنْ سطحِ البحرِ ( 8848m ) ،أحسبُ هذا الارتفاعَ بالكيلومتراتِ(km).

8.848Km
يُعدُّ صقرُ الشاهينِ منْ أكثرِ الجوارحِ انتشارًا في العالَمِ، ويبلغُ طولُ المسافةِ بينَ طرَفَيْ جناحَيْهِ في أثناءِ فَرْدِهِما ( 120cm ). أحسبُ هذهِ المسافةَ بوحدةِ المترِ (m).

1.2m

 

مثال 1 

إذا عرفتُ أنَّ طولَ ضلعِ المربّعِ في الشكلِ يساوي ( 5cm).أحسبُ المسافةَ التي يقطعُها جسمٌ عندَ انتقالِهِ منَ النقطةِ (a) إلى (b)، والإزاحةَ التي يحقِّقُها في الشكلِ الآتي:

                                                                
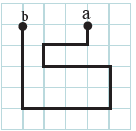
الحلُّ:
المسافةُ : طولُ المسارِ الكلّيِّ الذي تحرَّكَهُ الجسمُ (S):
S = 5 x17
= 85cm
الإزاحةُ: الفرقُ بينَ نقطةِ البدايةِ ونقطةِ النهايةِ (Δx):
Δ_x = x_b - x_a
= 15 cm
باتجاهِ الغربِ.

 

أتحقَّقُ: هلْ منَ الممكنِ أنْ يكونَ مقدارُ الإزاحةِ صفرًا؟ أوضِّحُ إجابتي بالرّسْمِ.

نعم، ذلك ممكن إذا تحرك الجسم وعاد إلى المكان نفسه، مثل حركة سيارة على الدوار عندما يتحرك دائرة كاملة، يجب الانتباه إلى أن تكون البداية والنهاية عند النقطة نفسها؛ حتى تكون الإزاحة تساوي صفرًا.

 

الربط بالحياة 

منْ مناسك الحجِّ عندَ المسلمينَ السَّعْيُ بينَ الصَّفا والْمَرْوَةِ؛ إذْ يبدأُ الحاجُّ منَ الصّفا وينتهي بالمروةِ قاطعًا ( 395m)، ويسمّى هذا شَوْطًا. فإذا بدأَ حاجٌّ السعيَ بالصفا وانتهى
بالمروةِ بعدَ قطعِ سبعةِ أشواطٍ، فما المسافةُ والإزاحةُ التي قطعَها الحاجُّ منْ بدايةِ السَّعيِ إلى نهايتِهِ؟

S = 7×395=2765 m
Δ =395 m

 

أبحثُ :أبحثُ عنْ كمّيّاتٍ فيزيائيَّةٍ متَّجهةٍ، ثمَّ أكتبُها في دفتري.

القوة، والسرعة، والتسارع

 

السرعةُ القياسيَّةُ Speed

• في سباقِ الجريِ نهتمُّ بمعرفةِ المسافةِ التي سيقطعُها المتسابقونَ، والزمنِ الذي يستغرقُهُ كلٌّ منْهُمْ في قطعِ هذهِ المسافةِ؛ فإذا قسمْنا المسافةَ المقطوعةَ على الزمنِ فإنَّ الناتجَ يمثلُ السرعةَ القياسيَّةَ، وهيَ كمّيّةٌ قياسيّةٌ تُحَدَّدُ بالمقدارِ فقطْ. 

 

• تُعرَّفُ السرعةُ القياسيةُ Speed لجسمٍ ما بأنَّها مقدارُ المسافةِ S التي يقطعُها جسمٌ ما في مدَّةٍ زمنيَّةٍ محدَّدةٍ  t، ويُرمَزُ إليْها بالرمزِ v. ورياضيًّا، فإنَّ:
  السرعةَ =المسافةَ المقطوعةَ ÷ الزمنِ الكُلّيِّ
  وتُكتَبُ العلاقةُ بالرموزِ    v = S÷ t
   
• تُقاسُ السرعةُ بوحدةِ مترٍ لكلِّ ثانيةٍ (m/s) ، أوْ كيلومترٍ لكلِّ ساعةٍ (km/h)
• يتحرَّكُ الجسمُ بسرعةٍ ثابتةٍ عندَما يقطعُ مسافاتٍ متساويةً في أزمنةٍ متساويةٍ. فنقولُ حينَها: إنَّ الجسمَ يتحرَّكُ حركةً منتظمةً Uniform Motion. فمثلً، إذا كنتُ أجلسُ بجانبِ والدي في السيارةِ، وراقبتُ عدّادَ السرعةِ مدَّةً منَ الزمنِ، ووجدتُ أنَّهُ يشيرُ إلى الرقمِ نفسِهِ؛ فهذا يعني أنَّ السيارةَ تتحرَّكُ بسرعةٍ ثابتةٍ.
• عندما أذهبُ إلى مدرستي فإنَّني أُسرِعُ أحيانًا، وأُبطِئُ أحيانًا أُخرى؛ نتيجةَ الازدحامِ، أوِ التّعبِ، أوْ حالةِ الطقسِ؛ أيْ إنَّ سرعتي تتغيَّرُ باستمرارٍ. فالجسمُ يتحرَّكُ بسرعةٍ مُتغيِّرَةٍ عندَما يقطعُ مسافاتٍ غيرَ متساويةٍ في أزمنةٍ متساويةٍ؛ لذا فإنَّنا نحسبُ ما يُسمّى السرعةَ القياسيّةَ المتوسّطةَ Average Speed ، وفي هذه الحالةِ نصفُ حركةَ الجسمِ بأنَّها حركةٌ غيرُ منتظمةٍ. ورياضيًّا، فإنَّ:

          السرعةَ المتوسّطةَ =المسافةَ الكليّةَ المقطوعةَ÷الزمنِ الكُلّيِّ المستغرَقِ

 

مثال 2 

كمِ المسافةُ التي تقطعُها سيارةٌ تتحرَّكُ بسرعةٍ ثابتةٍ مقدارُها ( 12m/s )، في ( 10 ) دقائقَ؟
الحلُّ:
نحتاجُ إلى تحويلِ الزمنِ منَ الدقائقِ إلى الثواني، علمًا أنََّ الدقيقةَ الواحدةَ تساوي ( 60 ) ثانيةً:
S = v×t
= 12 × 600
= 7200m

 

 

 

مثال 3

يقطعُ رجلٌ مسافةَ ( 450m ) بسرعةٍ متوسّطةٍ مقدارُها ( 3m/s ). ما الزمنُ الذي احتاجَ إليْهِ ليقطعَ هذهِ المسافةَ؟
الحلُّ:
نحتاجُ إلى تحويلِ الزمنِ منَ الدقائقِ إلى الثواني، علمًا أنََّ الدقيقةَ الواحدةَ تساوي ( 60 ) ثانيةً:
t = S÷v
= 450÷3
= 150s  

 

تجربة : قياسُ السرعةِ المتوسِّطةِ

الموادُّ والأدواتُّ: مترٌ، وساعةُ توقيتٍ.
ملحوظةٌ: منَ الممكنِ إجراءُ التجربةِ في ساحةِ المدرسةِ.
إرشاداتُ السلامةِ: أتعاملُ بحذَرٍ معَ الحافَةِ الحادّةِ لِمترِ القياسِ، وأتَّبعُ توجيهاتِ المعلِّمِ.
خطواتُ العملِ:
1. أجرِّبُ: أحدِّدُ على الأرضِ مسافةَ ( 5m ) ومسافةَ ( 10m ).
2. أتواصلُ: أطلبُ إلى زميلي أنْ يمشيَ كِلتا المسافتَيْنِ، ثمَّ أحسُبُ الزمنَ المستغرقَ في كلِّ حالةٍ باستخدامِ ساعةِ التوقيتِ.
3. أطبّقُ: أحسُبُ مقدارَ سرعةِ زميلي المتوسِّطةِ باستخدامِ معادلةِ السرعةِ.
4. أكرِّرُ القياسَ، لكنْ على مسافاتٍ أطوَلَ.
التحليلُ والاستنتاجُ:
1. أقارنُ بينَ مقدارِ سرعةِ زميلي في كلِّ الحالاتِ.

تختلف سرعة زميلي حسب الزمن المقطوع خلال المسافة المقطوعة 
2. أستنتجُ: هلْ يختلفُ مقدارُ سرعةِ زميلي معَ اختلافِ المسافةِ المقطوعةِ؟ لماذا؟

يتفاوت الطلبة في سرعتهم، فالطالب الأسرع هو الطالب الذي يقطع المسافة المطلوبة في وقت أقصر.

 

السرعةُ المتَّجِهَةُ Velocity

• يعتمدُ كثيرٌ منَ الأنشطةِ في حياتِنا، مثلِ الملاحةِ الجويّةِ، على معرفةِ الحالةِ الجويَّةِ، بما في ذلكَ معرفةُ مقدارِ سرعةِ الرياحِ واتجاهِها؛ لذلكَ تهتمُّ الأرصادُ الجويّةُ قياسِ سرعةِ الرياحِ وتحديدِ اتجاهِها. فمثلا، يمكنُ القولُ: تهبُّ رياحٌ شرقيّةٌ سرعتُها ( 60km/h ).
• تُسمّى السرعةُ التي تُحَدَّدُ بالمقدارِ والاتجاهِ السرعةَ المُتَّجِهَةَ Velocity ، وتُعرَّفُ بأنَّها الإزاحةُ ( Δx ) التي يحقِّقُها جسمٌ ما في مدَّةٍ زمنيّةٍ محدَّدةٍ (t)، ويُرمَزُ إليْها بالرمزِ (v ).
• يُعَبَّرُ عنِ السرعةِ المتّجهةِ رياضِيًّا بالعلاقة الآتية:

                                                                            v=Δx/t

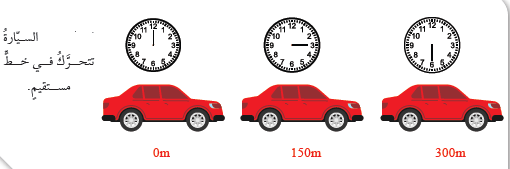
• عندَ ملاحظةِ الشكلِ أدناه نجدُ أنَّ السيارةَ تتحرَّكُ في خطٍّ مستقيمٍ، حيثُ تقطعُ ( 150m ) كلَّ ( 15s )، أيْ إنَّها تتحرَّكُ بسرعةٍ ثابتةٍ ( 10m/s ) باتجاهِ الشرقِ

                                                  

أبحثُ :أبحثُ عنْ حيواناتٍ أُخرى سرعتُها كبيرةٌ.

الغزال ، النمر ، الأسد 
 

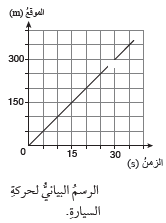
• يمكنُ وصفُ حركةِ السيارةِ باستخدامِ المنحنَياتِ البيانِيَّةِ، ومعرفةُ إنْ كانتْ حركتُها منتظمةً. فعندَما نرسُمُ بيانِيًّا (الموقعُ (x) – الزمنِ ( t)) نحصلُ على خطٍّ مستقيمٍ، فنستنتجُ منْ ذلكَ أنَّ حركةَ السيارةِ حركةٌ منتظمةٌ ، أنظر الشكل أدناه

                                                        

مثال 4 

يمثِّلُ الشكلُ منحنى (الموقعِ - الزّمنِ) لرجلٍ يقودُ درّاجتَهُ نحوَ الشمالِ، أصفُ حركةَ الرجلِ.

                                                                                                           
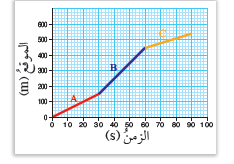
الحلُّ:
أستنتجُ منَ الشّكلِ أنَّ الرجلَ يتحرَّكُ حركةً غيرَ منتظمةٍ؛ إذْ إنَّ حركتَهُ في كلِّ مرحلةٍ استغرقَتْ ( 30s )، ولكنْ كانتِ الإزاحةُ المتحقِّقةُ مختلفةً؛ ففي المرحلةِ الأولى (A) كانَ مقدارُ الإزاحةِ 150m،وفي المرحلةِ الثانيةِ (B)كانَ مقدارُها 300m وفي المرحلةِ الأخيرةِ (C)كانَ مقدارُها 90m.إذا تأمَّلتُ الرسمَ البيانيَّ سأجِدُ أنَّ التغيُّرَ في موقعِ الرجلِ على دراجتِهِ (540m) في زمنِ ( 90s )، أيْ إنَّ متوسِّطَ سرعتِهِ ( 6m/s ).

 

أتحقَّقُ: ما أهمّيَّةُ الرسمِ البيانِيِّ لتغيُّرِ موقعِ الجسمِ معَ الزمنِ في وَصْفِ الحركةِ؟

يمكن من الرسم البياني معرفة هل الحركة منتظمة أو لا، ونحدد مقدار سرعة الجسم، وفترات التوقف عن الحركة.

 

أتأمل الشكل : أصفُ الحركةَ إذا علمتُ أنَّها لقطَّةٍ تتحرَّكُ. أُحدِّدُ الزمنَ التي توقَّفَتْ فيهِ القطَّةُ عنِ الحركةِ.

                                                                               

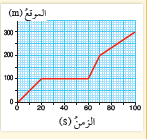
حركة القطة غير منتظمة، حيث تقطع مسافات غير متساوية في فترات زمنية متساوية، ويشير الشكل إلى توقف القطة في الفترة( 60 - s (20