الحركةُ Motion
- نعيشُ في عالَمٍ متحرِّكٍ؛ فالرّياحُ تهبُّ والسياراتُ تسيرُ، والأطفالُ يقضونَ وقتًا ممتعًا في الركضِ. لذلكَ فإنّنا نحتاجُ إلى طريقةٍ منظّمةٍ لوصفِ حركةِ الأجسامِ.
- الحركةُ Motion تَغَيُّرٌ مستمرٌّ في موقعِ جسمٍ ما مقارنةً بأجسامٍ ثابتةٍ حولَهُ.
- الموقعُ Position فهوَ بُعْدُ الجسمِ عنْ نقطةٍ إسنادٍ (نقطةٍ مرجعيةٍ).
- لتحديدِ موقعِ الجسمِ، ينبغي تحديدُ نقطةٍ مرجعيّةٍ نستندُ إليها، تسمّى نقطةَ إسنادٍ Reference Point
المسافةُ والإزاحةُ Distance and Displacement
- عندَما نريدُ وصفَ حركةِ جسمٍ ما يتحرَّكُ في خطٍّ مستقيمٍ فإنَّنا نحتاجُ إلى قياسِ المسافةِ التي يتحرَّكُها ، وإيجادِ الزّمنِ الذي يستغرقُهُ في قطعِ هذهِ المسافةَ.
- تُعرَّفُ المسافةُ Distance بأنّها الطولُ الكلّيُّ للمسارِ الذي يسلُكُهُ الجسمُ في أثناءِ انتقالِهِ بينَ نقطتينِ. وتُقاسُ بوحدةِ المترِ (m)، أوْ مضاعفاتِها، مثلِ: الكيلو مترِ (km)، أوْ أجزاءٍ منْها، مثلِ: السنتيمترِ (cm)، والملّيمترِ (mm).
- تعدُّ المسافةُ كميّةً قياسيَّةً Scalar Quantity ؛ أيْ إنّهُ يكفي لتحديدِها معرفةُ مقدارِها فقطْ؛ فنقولُ: إنَّ المسافةَ بينَ محافظةِ عمّانَ والزرقاءِ ( 30 km) تقريبًا، ويُرمَزُ إلى المسافةِ بالرمزِ (S).
- قدْ يوجدُ أكثرُ منْ مسارٍ يصلُ بينَ نقطتينِ. ويُسمى أقصرُ مسارٍ مستقيمٍ يصلُ بينَ نقطةِ بدايةِ الحركةِ ونهايتِها الإزاحةَ Displacement
- تعتبر الإزاحة كميَّةٌ متّجهةٌ Vector Quantity ؛ أيْ إنَّهُ يلزمُ لتحديدِها معرفةُ مقدارِها واتّجاهِها معًا، ويُرمَزُ إلى الإزاحةِ بالرمزِ (Δx).
- يُكتَبُ الرمزُ(Δ) ويُقرَأُ (دلتا) للتعبيرِ عنِ الفرقِ بينَ الموقعِ النهائيِّ للجسمِ وموقعِهِ في البدايةِ منْ دونِ الاهتمامِ بالمسارِ الذي سلكَهُ الجسمُ بينَهُما.
السرعةُ القياسيَّةُ Speed
- في سباقِ الجريِ نهتمُّ بمعرفةِ المسافةِ التي سيقطعُها المتسابقونَ، والزمنِ الذي يستغرقُهُ كلٌّ منْهُمْ في قطعِ هذهِ المسافةِ؛ فإذا قسمْنا المسافةَ المقطوعةَ على الزمنِ فإنَّ الناتجَ يمثلُ السرعةَ القياسيَّةَ، وهيَ كمّيّةٌ قياسيّةٌ تُحَدَّدُ بالمقدارِ فقطْ.
- تُعرَّفُ السرعةُ القياسيةُ Speed لجسمٍ ما بأنَّها مقدارُ المسافةِ S التي يقطعُها جسمٌ ما في مدَّةٍ زمنيَّةٍ محدَّدةٍ t، ويُرمَزُ إليْها بالرمزِ v. ورياضيًّا، فإنَّ:
السرعةَ =المسافةَ المقطوعةَ ÷ الزمنِ الكُلّيِّ
وتُكتَبُ العلاقةُ بالرموزِ v = S÷ t
- تُقاسُ السرعةُ بوحدةِ مترٍ لكلِّ ثانيةٍ (m/s) ، أوْ كيلومترٍ لكلِّ ساعةٍ (km/h)
- يتحرَّكُ الجسمُ بسرعةٍ ثابتةٍ عندَما يقطعُ مسافاتٍ متساويةً في أزمنةٍ متساويةٍ. فنقولُ حينَها: إنَّ الجسمَ يتحرَّكُ حركةً منتظمةً Uniform Motion. فمثلً، إذا كنتُ أجلسُ بجانبِ والدي في السيارةِ، وراقبتُ عدّادَ السرعةِ مدَّةً منَ الزمنِ، ووجدتُ أنَّهُ يشيرُ إلى الرقمِ نفسِهِ؛ فهذا يعني أنَّ السيارةَ تتحرَّكُ بسرعةٍ ثابتةٍ.
- عندما أذهبُ إلى مدرستي فإنَّني أُسرِعُ أحيانًا، وأُبطِئُ أحيانًا أُخرى؛ نتيجةَ الازدحامِ، أوِ التّعبِ، أوْ حالةِ الطقسِ؛ أيْ إنَّ سرعتي تتغيَّرُ باستمرارٍ. فالجسمُ يتحرَّكُ بسرعةٍ مُتغيِّرَةٍ عندَما يقطعُ مسافاتٍ غيرَ متساويةٍ في أزمنةٍ متساويةٍ؛ لذا فإنَّنا نحسبُ ما يُسمّى السرعةَ القياسيّةَ المتوسّطةَ Average Speed ، وفي هذه الحالةِ نصفُ حركةَ الجسمِ بأنَّها حركةٌ غيرُ منتظمةٍ. ورياضيًّا، فإنَّ:
السرعةَ المتوسّطةَ =المسافةَ الكليّةَ المقطوعةَ÷الزمنِ الكُلّيِّ المستغرَقِ
السرعةُ المتَّجِهَةُ Velocity
- يعتمدُ كثيرٌ منَ الأنشطةِ في حياتِنا، مثلِ الملاحةِ الجويّةِ، على معرفةِ الحالةِ الجويَّةِ، بما في ذلكَ معرفةُ مقدارِ سرعةِ الرياحِ واتجاهِها؛ لذلكَ تهتمُّ الأرصادُ الجويّةُ قياسِ سرعةِ الرياحِ وتحديدِ اتجاهِها. فمثلا، يمكنُ القولُ: تهبُّ رياحٌ شرقيّةٌ سرعتُها ( 60km/h ).
- تُسمّى السرعةُ التي تُحَدَّدُ بالمقدارِ والاتجاهِ السرعةَ المُتَّجِهَةَ Velocity ، وتُعرَّفُ بأنَّها الإزاحةُ ( Δx ) التي يحقِّقُها جسمٌ ما في مدَّةٍ زمنيّةٍ محدَّدةٍ (t)، ويُرمَزُ إليْها بالرمزِ (v ).
- يُعَبَّرُ عنِ السرعةِ المتّجهةِ رياضِيًّا بالعلاقة الآتية:
v=Δx/t
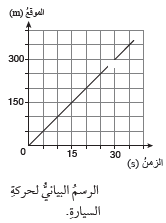
- يمكنُ وصفُ حركةِ السيارةِ مثلا باستخدامِ المنحنَياتِ البيانِيَّةِ، ومعرفةُ إنْ كانتْ حركتُها منتظمةً. فعندَما نرسُمُ بيانِيًّا (الموقعُ (x) – الزمنِ ( t)) نحصلُ على خطٍّ مستقيمٍ، فنستنتجُ منْ ذلكَ أنَّ حركةَ السيارةِ حركةٌ منتظمةٌ ، أنظر الشكل أدناه