أتحقق من فهمي
ص: 10
إذا كان :
a) أحدد مجال f(x)
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية كلها.
b) أجد قيمة كل من f(5)، و f(2).
بما أن إذن:
بما أن إذن:
c) أمثل الاقتران f(x) بيانيا، وأحدد مداه.
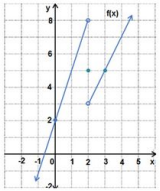
مدى الاقتران هو مجموعة الأعداد الحقيقية.
أتحقق من فهمي
ص: 11
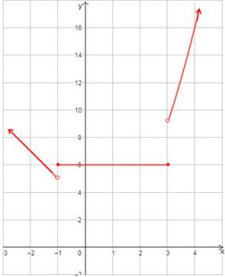
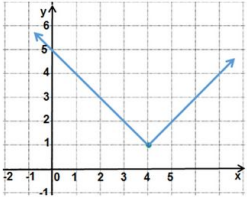
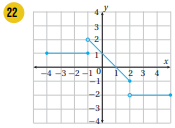
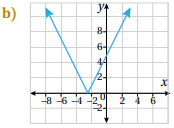
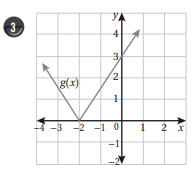
أكتب قاعدة الاقتران f(x) الممثل بيانيا في الشكل المجاور.
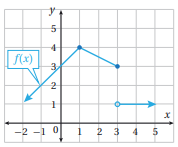
الجانب الأيسر من الرسم المقطع الصادي= 3، والميل=1، الجانب الأوسط الميل = ، وتمر بالنقطة ، الجانب الأيسر الاقتران ثابت فيصبح الاقتران كما يأتي:
أتحقق من فهمي
ص: 12
زادت شركة رواتب موظفيها الشهرية وفق الأسس الآتية: الرواتب التي تقل عن 400 دينار زيدت بنسبة ، والرواتب من 400 دينار إلى أقل من 600 دينار زيدت بنسبة ، والرواتب من 600 دينار وأكثر زيدت 50 دينارا. أكتب اقترانا متشعبا لحساب الراتب الجديد لموظفي الشركة.
الفئة الأولى تأخذ راتبها %100 بالإضافة إلى %20 ما مجموعه %120 من الراتب
الفئة الثانية تأخذ راتبها %100 بالإضافة إلى %10 ما مجموعه %110 من الراتب
الفئة الثالثة فقط إضافة 50 دينار على الراتب.
أتحقق من فهمي
ص: 14
أعيد تعريف كل من الاقترانات الآتية:
نساوي ما داخل المطلق بالصفر ونحل المعادلة ونختبر الحلول على خط الأعداد
أتحقق من فهمي
ص: 16
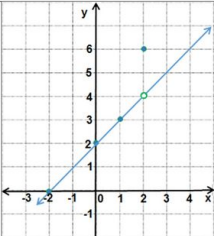
أمثل بيانيا كل اقتران مما يأتي، محددا مجاله ومداه:
المجال مجموعة الأعداد الحقيقية كلها، والمدى هو ، أو الفترة .
المجال مجموعة الأعداد الحقيقية كلها، والمدى هو ، أو الفترة
أتحقق من فهمي
ص: 18
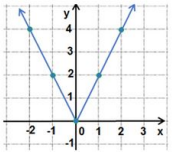
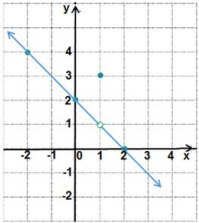
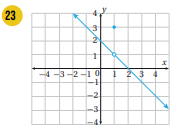
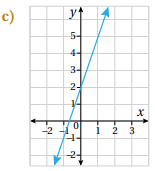
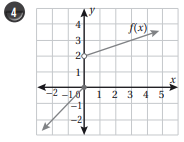
أكتب قاعدة اقتران القيمة المطلقة f(x) الممثل بيانيا في الشكل المجاور.
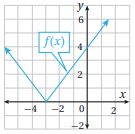
الميل هو الرأس
أتدرب وأحل المسائل
إذا كان ، فأجد كلا من:
بما أن
بما أن
بما أن
بما أن
بما أن
بما أن
أعيد تعريف كل من الاقترانات الآتية:
أمثل كلا من الاقترانات الآتية بيانيا، وأحدد مجالها ومداها:
المجال مجموعة الأعداد الحقيقية، المدى أو الفترة .
المجال مجموعة الأعداد الحقيقية، المدى
المجال مجموعة الأعداد الحقيقية، المدى أو الفترة .
المجال مجموعة الأعداد الحقيقية، المدى أو الفترة .
المجال مجموعة الأعداد الحقيقية، المدى مجموعة الأعداد الحقيقية.
المجال مجموعة الأعداد الحقيقية، المدى مجموعة الأعداد الحقيقية
المجال: مجموعة الأعداد الحقيقية، المدى:
المجال مجوعة الأعداد الحقيقية، المدى أو الفترة .
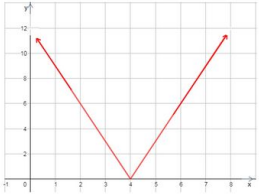
المجال مجموعة الأعداد الحقيقية، المدى أو الفترة .
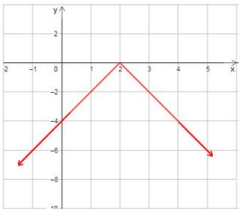
المجال مجموعة الأعداد الحقيقية، المدى أو الفترة .
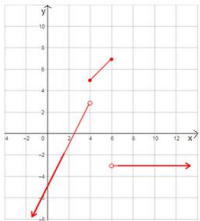
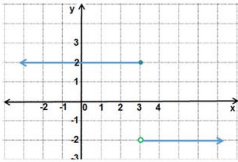
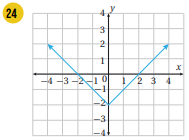
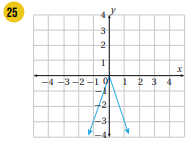
أكتب قاعدة الاقتران المتشعب الممثل بيانيا في كل من الأشكال الآتية:
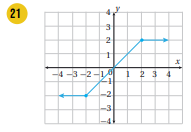
الجهة اليمنى اقتران ثابت، الجهة الوسطى مقطع الصادات =0، والميل=1، الجهة اليسرى اقتران ثابت
الجهة اليمنى اقتران ثابت، الجهة الوسطى مقطع الصادات =1، والميل=1-، الجهة اليسرى اقتران ثابت
مقطع الصادات =2، مقطع السينات=2، والميل=1-، وصورة الاقتران عند x=1 تساوي 3
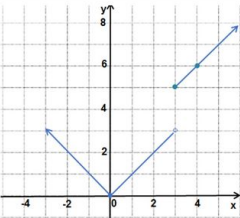
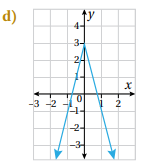
أكتب قاعدة اقتران القيمة المطلقة الممثل بيانيا في كل من الأشكال الآتية:
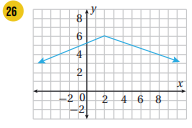
27) أعود إلى مسألة اليوم وأكتب الاقتران المتشعب الذي يمكنني استعماله لحساب ثمن المياه لأي كمية مستهلكة.
خيمة: يمثل منحنى الاقتران حافتي الوجه الأمامي لخيمة، ويمثل العمود الذي يتوسط الوجه الأمامي للخيمة المحور y، وأما المحور x فيمثله سطح الأرض.
28) أمثل الاقتران بيانيا.
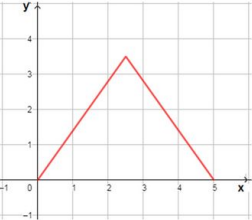
29) أجد مجال الاقتران ومداه.
مجال هذا الاقتران هو ، ومداه .
30) أعمال: يتقاضى مندوب مبيعات راتبا شهريا مقداره 500 دينار، وعمولة بنسبة لأول 20000 دينار من مبيعاته الشهرية، وإذا زادت مبيعاته على 20000 دينار يأخذ عمولة بنسبة مما يزيد على 20000 دينار. أكتب اقترانا متشعبا لحساب الدخل الشهري لهذا المندوب.
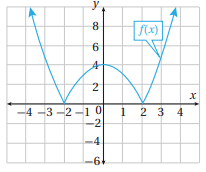
عاصفة: تبدأ العاصفة المطرية بالهطل على شكل رذاذ ثم يزداد معدل الهطل، ثم تعود ثانية للهطل على شكل رذاذ، ويمثل الاقتران ، معدل الهطل r (بالإنش لكل ساعة)، حيث t الزمن بالساعات منذ بداية الهطل.
31) أمثل اقتران معدل الهطل بيانيا.
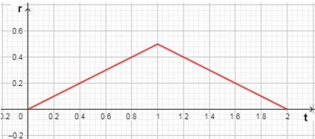
32) أجد كم ساعة استمر الهطل.
استمر الهطل ساعتان لأنه توقف بعد ساعتين، يقطع المنحنى المحور الأفقي عند 0، و 2
33) بعد كم ساعة كان أعلى معدل هطل؟ أبرر إجابتي.
كان أعلى معدل هطل بعد ساعة من بدئه، يبين الرسم أن القيمة العظمى عند
مهارات التفكير العليا
34) تبرير: أي الآتية تمثل منحنى الاقتران ؟ أبرر إجابتي:
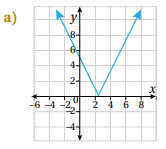
a، لأن الرأس عند ، ومفتوح للأعلى
35) تبرير: هل تمثل العلاقة المتشعبة الآتية اقترانا؟ أبرر إجابتي.
لا تشكل اقترانا بسب تداخل المجالين الجزئيين، فالفترة تقع في كل من و فسيكون للعدد 1 مثلا صورتان هما 2-،و 1 وهذا يناقض تعريف الاقتران.
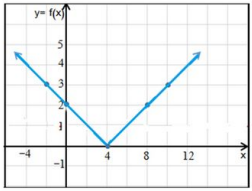
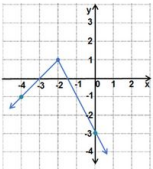
36) تبرير: أكتب قاعدة الاقتران f(x) الممثل بيانيا في الشكل المجاور مبررا إجابتي.
لأن الرسم هو لقطع مكافئ يقطع المحور x عند 2-، 2، وعكس الجزء الواقع تحت المحور x حول المحور x.
37) مسألة مفتوحة: أكتب اقتران قيمة مطلقة f(x) بحيث يكون f(4)= -5.
تحد: يمكن كتابة المقدار على صورة
38) أجد قيمة كل من p، و q.
39) أجد إحداثي كل من نقطتي تقاطع المنحنى مع محور x.
إحداثيا نقطتي تقاطع منحنى f(x) مع المحور x هما .
حل أسئلة كتاب التمارين
أعيد تعريف كل من الاقترانين الآتيين:
أكتب قاعدة الاقتران المعطى تمثيله البياني، في كل مما يأتي:
أمثل كلا من الاقترانات الآتية بيانيا، وأحدد مجاله ومداه:
| 5 | 3 | 3 | 1 | x |
| 8 | 6 | 5 | -1 | y |
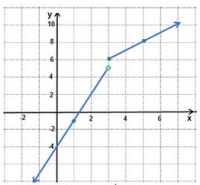
المجال: مجموعة الأعداد الحقيقية
المدى:
| 5 | 4 | 4 | 1 | 0 | 1- | x |
| 7 | 6 | 5 | 5 | 3 | 5 | y |
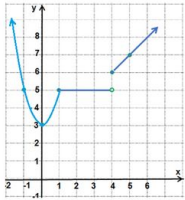
المجال: مجموعة الأعداد الحقيقية
المدى: أو الفترة
إحداثيات الرأس ، أختار نقطة قبله ونقطة بعده لأكون الجدول:
| x | 2 | 3 | 4 |
| y | 5 | 3 | 5 |
وأعين النقاط وأرسم شكل v.
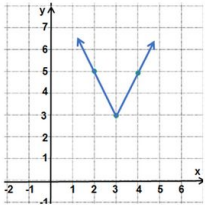
المجال: مجموعة الأعداد الحقيقية
المدى: أو الفترة .
أجد الإحداثي x لرأس القطع المكافئ ومقطعه من المحورين وقيمتين أخريين أعوضها في معادلة الاقتران لأكون الجدول:
| x | 3- | 2- | 0 | 1 | 4 | 5 |
| y | 7- | 0 | 6- | 9- | 0 | 7- |
وأعين النقاط وأرسم المنحنى.
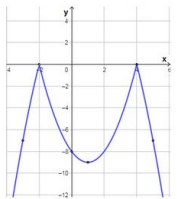
المجال: مجموعة الأعداد الحقيقية
المدى: أو الفترة .
9) كهرباء: تزود شركة الكهرباء القطاع التجاري بالطاقة الكهربائية مقابل 1.20 دينار شهريا (رسوما ثابتة)، يضاف إليها 0.121 دينار لكل كيلو واط ساعة لأول 2000 كيلو واط ساعة في الشهر، و 0.176 دينار لكل واط ساعة من كمية الاستهلاك الزائدة على 2000 كيلو واط ساعة في الشهر. أكتب الاقتران الذي يعطى قيمة فاتورة الكهرباء بدلالة كمية الاستهلاك x كيلو واط ساعة شهريا.