lesson questions solve - Grade التوجيهي علمي - رياضيات فصل ثاني - JO Academy school

الدرس الثالث: التكامل بالكسور الجزئية .

التحقق من الفهم ص 49

أجد كلاً من التكاملين الآتيين:

$a \int \frac{x - 7}{x^{2} - x - 6} d x S o l u t i o n : \frac{x - 7}{x^{2} - x - 6} = \frac{a}{x - 3} + \frac{b}{x + 2} x - 7 = a (x + 2) + b (x - 3) w h e n x = 3 \Rightarrow 3 - 7 = 5 a \Rightarrow a = \frac{- 4}{5} w h e n x = - 2 \Rightarrow - 2 - 7 = - 5 b \to b = \frac{9}{5} \frac{x - 7}{x^{2} - x - 6} = \frac{\frac{- 4}{5}}{x - 3} + \frac{\frac{9}{5}}{x + 2} \int \frac{x - 7}{x^{2} - x - 6} d x = \frac{- 4}{5} \int \frac{1}{x - 3} d x + \frac{9}{5} \int \frac{1}{x + 2} d x = \frac{- 4}{5} l n (x - 3) + \frac{9}{5} l n (x + 2) + c$

$b \int \frac{3 x - 1}{x^{2} - 1} d x S o l u t i o n : \frac{3 x - 1}{x^{2} - 1} = \frac{a}{x - 1} + \frac{b}{x + 1} 3 x - 1 = a (x + 1) + b (x - 1) w h e n x = 1 \Rightarrow 3 - 1 = 2 a \Rightarrow a = 2 w h e n x = - 1 \Rightarrow - 3 - 1 = - 2 b \Rightarrow b = 2 \frac{3 x - 1}{x^{2} - 1} = \frac{1}{x - 1} + \frac{2}{x + 1} \int \frac{3 x - 1}{x^{2} - 1} d x = \int \frac{1}{x - 1} d x + 2 \int \frac{1}{x + 1} d x = l n (x - 1) + 2 l n (x + 1) + c$

التحقق من الفهم ص 51

أجد كلاً من التكاملين الآتيين:

$a \int \frac{x + 4}{(2 x - 1) {(x - 1)}^{2}} d x S o l u t i o n : \frac{x + 4}{(2 x - 1) {(x - 1)}^{2}} = \frac{a}{2 x - 1} + \frac{b}{x - 1} + \frac{c}{{(x - 1)}^{2}} x + 4 = a {(x - 1)}^{2} + b (2 x - 1) (x - 1) + c (2 x - 1) w h e n x = \frac{1}{2} \Rightarrow \frac{9}{2} = \frac{a}{4} \Rightarrow a = 18 w h e n x = 1 \Rightarrow 5 = c \Rightarrow c = 5 w h e n x = 0 \Rightarrow 4 = 18 + b - 5 \Rightarrow b = - 9 \int \frac{x + 4}{(2 x - 1) {(x - 1)}^{2}} d x = 18 \int \frac{1}{2 x - 1} d x - 9 \int \frac{1}{x - 1} d x + 5 \int \frac{1}{{(x - 1)}^{2}} d x = 9 \int \frac{2}{2 x - 1} d x - 9 \int \frac{1}{x - 1} d x + 5 \int \frac{1}{{(x - 1)}^{2}} d x = 9 l n (2 x - 1) - 9 l n (x - 1) - \frac{5}{x - 1} + c$

$b \int \frac{x^{2} - 2 x - 4}{x^{3} - 4 x^{2} + 4 x} d x S o l u t i o n : \frac{x^{2} - 2 x - 4}{x^{3} - 4 x^{2} + 4 x} = \frac{a}{x} + \frac{b}{x - 2} + \frac{c}{{(x - 2)}^{2}} x^{2} - 2 x - 4 = a {(x - 2)}^{2} + b x (x - 2) + c x w h e n x = 0 \Rightarrow - 4 = 4 a \to a = - 1 w h e n x = 2 \Rightarrow - 4 = 2 c \to c = - 2 w h e n x = - 2 \Rightarrow 4 = 16 a + 8 b - 2 c 2 = - 16 - 32 b + 4 \to b = 2 \int \frac{x^{2} - 2 x - 4}{x^{3} - 4 x^{2} + 4 x} d x = l n (x) + 2 l n (x - 2) + \frac{2}{x - 2} + c$

التحقق من الفهم ص 52

أجد كلاً من التكاملين الآتيين:

$a \int \frac{3 x + 4}{(x - 3) (x^{2} + 4)} d x S o l u t i o n : \frac{3 x + 4}{(x - 3) (x^{2} + 4)} = \frac{a}{x - 3} + \frac{b x + c}{x^{2} + 4} 3 x + 4 = a (x^{2} + 4) + (b x + c) (x - 3) w h e n x = 3 \Rightarrow 13 = 13 a \Rightarrow a = 1 w h e n x = 0 \Rightarrow 4 = 4 - 3 c \Rightarrow c = 0 w h e n x = 1 \Rightarrow 7 = 5 + - 2 b \Rightarrow b = - 1 \int \frac{3 x + 4}{(x - 3) (x^{2} + 4)} d x = \int \frac{1}{x - 3} d x - \frac{1}{2} \int \frac{2 x}{x^{2} + 4} d x = l n (x - 3) - \frac{1}{2} l n (x^{2} + 4) + c$

$b \int \frac{7 x^{2} - x + 1}{x^{3} + 1} d x S o l u t i o n : \frac{7 x^{2} - x + 1}{x^{3} + 1} = \frac{A}{x + 1} + \frac{B x + c}{x^{2} - x + 1} 7 x^{2} - x + 1 = A (x^{2} - x + 1) + (B x + c) (x + 1) w h e n x = - 1 \Rightarrow 9 = 3 A \Rightarrow A = 3 w h e n x = 0 \Rightarrow 1 = A + C \Rightarrow 1 = 3 + C \Rightarrow C = - 2 w h e n x = 1 \Rightarrow 7 = 3 + 2 B - 4 \Rightarrow 8 = 2 B \Rightarrow B = 4 \int \frac{7 x^{2} - x + 1}{x^{3} + 1} d x = \int \frac{3}{x + 1} d x + \int \frac{4 x - 2}{x^{2} - x + 1} d x = 3 l n (x + 1) + 2 \int \frac{2 x - 1}{x^{2} - x + 1} d x = 3 l n (x + 1) + 2 l n (x^{2} - x + 1) + c$

التحقق من الفهم ص 53

أجد كلاً من التكاملين الآتيين:

$a \int \frac{4 x^{3} - 5}{2 x^{2} - x - 1} d x S o l u t i o n : \frac{4 x^{3} - 5}{2 x^{2} - x - 1} = 2 x + 1 + \frac{3 x - 4}{2 x^{2} - x - 1} \frac{3 x - 4}{2 x^{2} - x - 1} = \frac{A}{2 x + 1} + \frac{B}{x - 1} 3 x - 4 = A (x - 1) + B (2 x + 1) w h e n x = - \frac{1}{2} \Rightarrow - \frac{11}{2} = - \frac{3}{2} A \Rightarrow A = \frac{11}{3} w h e n x = 1 \Rightarrow - 1 = 3 B \Rightarrow B = - \frac{1}{3} \int \frac{3 x - 10}{x^{2} - 7 x + 12} d x = \int (2 x + 1) d x + \frac{11}{3} \int \frac{1}{2 x + 1} d x - \frac{1}{3} \int \frac{1}{x - 1} d x = 2 x^{2} + x + \frac{11}{3} l n (2 x + 1) - \frac{1}{3} l n (x - 1) + c$

$b \int \frac{x^{2} + x - 1}{x^{2} - x} d x S o l u t i o n : \frac{x^{2} + x - 1}{x^{2} - x} = 1 + \frac{2 x - 1}{x^{2} - x} \int \frac{x^{2} + x - 1}{x^{2} - x} d x = \int 1 d x + \int \frac{2 x - 1}{x^{2} - x} d x = x + l n (x^{2} - x) + c$

التحقق من الفهم ص 54

أجد كلاً من التكاملين الآتيين:

$a \int_{3}^{4} \frac{2 x^{3} + x^{2} - 2 x - 4}{x^{2} - 4} d x S o l u t i o n : \frac{2 x^{3} + x^{2} - 2 x - 4}{x^{2} - 4} = \frac{2 x^{3} - 2 x}{x^{2} - 4} + \frac{x^{2} - 4}{x^{2} - 4} = \frac{6 x}{x^{2} - 4} + 2 x + 1 \int \frac{2 x^{3} + x^{2} - 2 x - 4}{x^{2} - 4} d x = \int \frac{6 x}{x^{2} - 4} d x + \int (2 x + 1) d x \int \frac{2 x^{3} + x^{2} - 2 x - 4}{x^{2} - 4} d x = 3 \int \frac{2 x}{x^{2} - 4} d x + \int (2 x + 1) d x = 3 \ln (x^{2} - 4) + x^{2} + x + c 4 3 = (3 \ln (12) + 20) - (3 l n (8) - 12) = 3 l n (12) - 3 n (8) + 8$

$b \int_{5}^{6} \frac{3 x - 10}{x^{2} - 7 x + 12} d x S o l u t i o n : \frac{3 x - 10}{x^{2} - 7 x + 12} = \frac{A}{x - 3} + \frac{B}{x - 4} 3 x - 10 = A (x - 4) + B (x - 3) w h e n x = 4 \Rightarrow 2 = B \Rightarrow B = 2 w h e n x = 3 \Rightarrow - 1 = - A \Rightarrow A = 1 \int \frac{3 x - 10}{x^{2} - 7 x + 12} d x = \int \frac{1}{x - 3} d x + 2 \int \frac{1}{x - 4} d x = l n (x - 3) + 2 l n (x - 4) 6 5 = l n (3) + 2 l n (2) - l n (2) - 2 l n (1) = l n (3) + l n (2) = l n (1.5)$

التحقق من الفهم ص 57

أجد كلاً من التكاملين الآتيين:

$a \int \frac{s e c^{2} x}{t a n^{2} x - 1} d x S o l u t i o n : l e t u = t a n x \Rightarrow d x = \frac{d u}{s e c^{2} x} \int \frac{s e c^{2} x}{t a n^{2} x - 1} d x = \int \frac{s e c^{2} x}{u^{2} - 1} \frac{d u}{s e c^{2} x} = \int \frac{1}{u^{2} - 1} d u \frac{1}{u^{2} - 1} = \frac{A}{u - 1} + \frac{B}{u + 1} 1 = A (u + 1) + B (u - 1) w h e n u = - 1 \Rightarrow 1 = - 2 B \Rightarrow B = - \frac{1}{2} w h e n u = 1 \Rightarrow 1 = 2 A \Rightarrow A = \frac{1}{2} \int \frac{1}{u^{2} - 1} d x = \frac{1}{2} \int \frac{1}{u - 1} d u - \frac{1}{2} \int \frac{1}{u + 1} d u = \frac{1}{2} l n (u - 1) - \frac{1}{2} l n (u + 1) = \frac{1}{2} l n (t a n x - 1) - \frac{1}{2} l n (t a n x + 1) + c$

$b \int \frac{e^{x}}{(e^{x} - 1) (e^{x} + 4)} d x S o l u t i o n : l e t u = e^{x} \Rightarrow d x = \frac{d u}{e^{x}} \int \frac{e^{x}}{(e^{x} - 1) (e^{x} + 4)} d x = \int \frac{e^{x}}{(u - 1) (u + 4)} \frac{d u}{e^{x}} = \int \frac{1}{(u - 1) (u + 4)} d u \frac{1}{(u - 1) (u + 4)} = \frac{A}{u - 1} + \frac{B}{u + 4} 1 = A (u + 4) + B (u - 1) w h e n u = - 4 \Rightarrow 1 = - 5 B \Rightarrow B = - \frac{1}{5} w h e n u = 1 \Rightarrow 1 = 5 A \Rightarrow A = \frac{1}{5} \int \frac{1}{(u - 1) (u + 4)} d x = \frac{1}{5} \int \frac{1}{u - 1} d u - \frac{1}{5} \int \frac{1}{u + 4} d u = \frac{1}{5} l n (u - 1) - \frac{1}{5} l n (u + 4) = \frac{1}{2} l n (e^{x} - 1) - \frac{1}{2} l n (e^{x} + 4) + c$

تمارين ومسائل

أجد كلاً من التكاملات الآتية:

$1 \int \frac{x - 10}{x (x + 5)} d x S o l u t i o n : \frac{x - 10}{x (x + 5)} = \frac{a}{x} + \frac{b}{x + 5} x - 10 = a (x + 5) + b (x) w h e n x = 0 \Rightarrow - 10 = 5 a \Rightarrow a = - 2 w h e n x = - 5 \Rightarrow - 15 = - 5 b \Rightarrow b = 3 \int \frac{x - 10}{x (x + 5)} d x = - 2 \int \frac{1}{x} d x + 3 \int \frac{1}{x + 5} d x = - 2 l n (x) + 3 l n (x + 5) + c$

$2 \int \frac{2}{x^{2} - 1} d x S o l u t i o n : \frac{2}{x^{2} - 1} = \frac{a}{x - 1} + \frac{b}{x + 1} 2 = a (x + 1) + b (x - 1) w h e n x = 1 \Rightarrow 2 = 2 a \Rightarrow a = 1 w h e n x = - 1 \Rightarrow 2 = - 2 b \Rightarrow b = 1 \int \frac{2}{x^{2} - 1} d x = \int \frac{1}{x - 1} d x + \int \frac{1}{x + 1} d x = l n (x - 1) + l n (x + 1) + c$

$3 \int \frac{4}{(x - 2) (x - 4)} d x S o l u t i o n : \frac{4}{(x - 2) (x - 4)} = \frac{a}{x - 2} + \frac{b}{x - 4} 4 = a (x - 4) + b (x - 2) w h e n x = 2 \Rightarrow 4 = - 2 a \Rightarrow a = - 2 w h e n x = 4 \Rightarrow 4 = 2 b \Rightarrow b = 2 \int \frac{4}{(x - 2) (x - 4)} d x = - 2 \int \frac{1}{x - 2} d x + 2 \int \frac{1}{x - 4} d x = - 2 l n (x - 2) + 2 l n (x - 4) + c$

$4 \int \frac{3 x + 4}{x^{2} + x} d x S o l u t i o n : \frac{3 x + 4}{x^{2} + x} = \frac{a}{x} + \frac{b}{x + 1} 3 x + 4 = a (x + 1) + b (x) w h e n x = 0 \Rightarrow 4 = a \Rightarrow a = 4 w h e n x = - 1 \Rightarrow 1 = - b \Rightarrow b = - 1 \int \frac{3 x + 4}{x^{2} + x} d x = 4 \int \frac{1}{x} d x - \int \frac{1}{x + 1} d x = 4 l n (x) - l n (x + 1) + c$

$5 \int \frac{x^{2}}{x^{2} - 4} d x S o l u t i o n : \frac{x^{2}}{x^{2} - 4} = \frac{x^{2} - 4}{x^{2} - 4} + \frac{4}{x^{2} - 4} \frac{x^{2}}{x^{2} - 4} = 1 + \frac{4}{x^{2} - 4} \frac{4}{x^{2} - 4} = \frac{a}{x - 2} + \frac{b}{x + 2} 4 = a (x + 2) + b (x - 2) w h e n x = 2 \Rightarrow 4 = 4 a \Rightarrow a = 1 w h e n x = - 2 \Rightarrow 4 = - 4 b \Rightarrow b = - 1 \int \frac{4}{x^{2} - 4} d x = \int 1 d x + \int \frac{1}{x - 2} d x - \int \frac{1}{x + 2} d x = x + l n (x - 2) - l n (x + 2) + c$

$6 \int \frac{3 x - 6}{x^{2} + x - 2} d x S o l u t i o n : \frac{3 x - 6}{x^{2} + x - 2} = \frac{a}{x + 2} + \frac{b}{x - 1} 3 x - 6 = a (x - 1) + b (x + 2) w h e n x = - 2 \Rightarrow - 12 = - 3 a \Rightarrow a = 4 w h e n x = 1 \Rightarrow - 3 = 3 b \Rightarrow b = - 1 \int \frac{3 x - 6}{x^{2} + x - 2} d x = 4 \int \frac{1}{x + 2} d x - \int \frac{1}{x - 1} d x = 4 l n (x + 2) - l n (x - 1) + c$

$7 \int \frac{4 x + 10}{4 x^{2} - 4 x - 3} d x S o l u t i o n : \frac{4 x + 10}{4 x^{2} - 4 x - 3} = \frac{a}{2 x - 3} + \frac{b}{2 x + 1} 4 x + 10 = a (2 x + 1) + b (2 x - 3) w h e n x = \frac{3}{2} \Rightarrow 16 = 4 a \Rightarrow a = 4 w h e n x = - \frac{1}{2} \Rightarrow 8 = - 4 b \Rightarrow b = - 2 \int \frac{4 x + 10}{4 x^{2} - 4 x - 3} d x = 4 \int \frac{1}{2 x - 3} d x - 2 \int \frac{1}{2 x + 1} d x = \frac{4}{2} \int \frac{2}{2 x - 3} d x - \frac{2}{2} \int \frac{2}{2 x + 1} d x = 2 l n (2 x - 3) - l n (2 x + 1) + c$

$8 \int \frac{2 x^{2} + 9 x - 11}{x^{3} + 2 x^{2} - 5 x - 6} d x S o l u t i o n : \frac{2 x^{2} + 9 x - 11}{x^{3} + 2 x^{2} - 5 x - 6} = \frac{a}{x - 2} + \frac{b}{x + 1} + \frac{c}{x + 3} 2 x^{2} + 9 x - 11 = a (x + 1) (x + 3) + b (x - 2) (x + 3) + c (x - 2) (x + 1) w h e n x = 2 \Rightarrow 15 = 15 a \Rightarrow a = 1 w h e n x = - 1 \Rightarrow - 18 = - 6 b \Rightarrow b = 3 w h e n x = - 3 \Rightarrow - 20 = 10 c \Rightarrow c = - 2 \int \frac{2 x^{2} + 9 x - 11}{x^{3} + 2 x^{2} - 5 x - 6} d x = \int \frac{1}{x - 2} d x + 3 \int \frac{1}{x + 1} d x - 2 \int \frac{1}{x + 3} d x = l n (x - 2) + 3 l n (x + 1) - 2 l n (x + 3) + c$

$9 \int \frac{4 x}{x^{2} - 2 x - 3} d x S o l u t i o n : \frac{4 x}{x^{2} - 2 x - 3} = \frac{a}{x - 3} + \frac{b}{x + 1} 4 x = a (x + 1) + b (x - 3) w h e n x = 3 \Rightarrow 12 = 4 a \Rightarrow a = 3 w h e n x = - 1 \Rightarrow - 4 = - 4 b \Rightarrow b = 1 \int \frac{4 x}{x^{2} - 2 x - 3} d x = 3 \int \frac{1}{x - 3} d x + \int \frac{1}{x + 1} d x = 3 l n (x - 3) + l n (x + 1) + c$

$10 \int \frac{8 x^{2} - 19 x + 1}{(2 x + 1) {(x - 2)}^{2}} d x S o l u t i o n : \frac{8 x^{2} - 19 x + 1}{(2 x + 1) {(x - 2)}^{2}} = \frac{a}{2 x + 1} + \frac{b}{x - 2} + \frac{c}{{(x - 2)}^{2}} 8 x^{2} - 19 x + 1 = a {(x - 2)}^{2} + b (2 x + 1) (x - 2) + c (2 x + 1) w h e n x = - \frac{1}{2} \Rightarrow \frac{25}{2} = \frac{25}{4} a \Rightarrow a = 2 w h e n x = 2 \Rightarrow - 5 = 5 c \Rightarrow c = - 1 w h e n x = 0 \Rightarrow 1 = 8 - 2 b - 1 \Rightarrow b = 3 \int \frac{8 x^{2} - 19 x + 1}{(2 x + 1) {(x - 2)}^{2}} d x = \int \frac{2}{2 x + 1} d x + 3 \int \frac{1}{x - 2} d x - \int \frac{1}{{(x - 2)}^{2}} d x = l n (2 x + 1) + 3 l n (x - 2) + \frac{1}{(x - 2)} + c$

$11 \int \frac{9 x^{2} - 3 x + 2}{9 x^{2} - 4} d x S o l u t i o n : \frac{9 x^{2} - 3 x + 2}{9 x^{2} - 4} = \frac{9 x^{2} - 4}{9 x^{2} - 4} + \frac{- 3 x + 6}{9 x^{2} - 4} \frac{9 x^{2} - 3 x + 2}{9 x^{2} - 4} = 1 + \frac{- 3 x + 6}{9 x^{2} - 4} \frac{- 3 x + 6}{9 x^{2} - 4} = \frac{a}{3 x - 2} + \frac{b}{3 x + 2} - 3 x + 6 = a (3 x + 2) + b (3 x - 2) w h e n x = \frac{2}{3} \Rightarrow 4 = 4 a \Rightarrow a = 1 w h e n x = - \frac{2}{3} \Rightarrow 8 = - 4 b \Rightarrow b = - 2 \int \frac{9 x^{2} - 3 x + 2}{9 x^{2} - 4} d x = \int 1 d x + \int \frac{1}{3 x - 2} d x - 2 \int \frac{1}{3 x + 2} d x = \int 1 d x + \frac{1}{3} \int \frac{3}{3 x - 2} d x - \frac{2}{3} \int \frac{3}{3 x + 2} d x = x + \frac{1}{3} l n (3 x - 2) - \frac{2}{3} l n (3 x + 2) + c$

$12 \int \frac{x^{3} + 2 x^{2} + 2}{x^{2} + x} d x S o l u t i o n : \frac{x^{3} + 2 x^{2} + 2}{x^{2} + x} = (x + 1) + \frac{2 - x}{x^{2} + x} \frac{2 - x}{x^{2} + x} = \frac{a}{x} + \frac{b}{x + 1} 2 - x = a (x + 1) + b (x) w h e n x = 0 \Rightarrow 2 = a \Rightarrow a = 2 w h e n x = - 1 \Rightarrow 3 = - b \Rightarrow b = - 3 \int \frac{x^{3} + 2 x^{2} + 2}{x^{2} + x} d x = \int (x + 1) d x + 2 \int \frac{1}{x} d x - 3 \int \frac{1}{x + 1} d x = \frac{x^{2}}{2} + x + 2 l n (x) - 3 l n (x + 1) + c$

$13 \int \frac{x^{2} + x + 2}{3 - 2 x - x^{2}} d x S o l u t i o n : - \frac{x^{2} + x + 2}{x^{2} + 2 x - 3} = - \frac{x^{2} + 2 x - 3}{x^{2} + 2 x - 3} + \frac{- x + 5}{x^{2} + 2 x - 3} - \frac{x^{2} + x + 2}{x^{2} + 2 x - 3} = - 1 + \frac{- x + 5}{x^{2} + 2 x - 3} \frac{- x + 5}{x^{2} + 2 x - 3} = \frac{a}{x - 1} + \frac{b}{x + 3} - x + 5 = a (x + 3) + b (x - 1) w h e n x = 1 \Rightarrow 4 = 4 a \Rightarrow a = 1 w h e n x = - 3 \Rightarrow 8 = - 4 b \Rightarrow b = - 2 \int \frac{x^{2} + x + 2}{x^{2} + 2 x - 3} d x = \int (- 1) d x + \int \frac{1}{x - 1} d x - 2 \int \frac{1}{x + 3} d x \int \frac{x^{2} + x + 2}{3 - 2 x - x^{2}} d x = x - l n (x - 1) + 2 l n (x + 3) + c$

$14 \int \frac{2 x - 4}{(x + 2) (x^{2} + 4)} d x S o l u t i o n : \frac{2 x - 4}{(x + 2) (x^{2} + 4)} = \frac{a}{x + 2} + \frac{b x + c}{x^{2} + 4} 2 x - 4 = a (x^{2} + 4) + (b x + c) (x + 2) w h e n x = - 2 \Rightarrow - 8 = 8 a \Rightarrow a = - 1 w h e n x = 0 \Rightarrow - 4 = 4 a + 2 c \Rightarrow c = 0 w h e n x = 1 \Rightarrow - 2 = - 5 + 3 b \Rightarrow b = 1 \int \frac{2 x - 4}{(x + 2) (x^{2} + 4)} d x = - \int \frac{1}{x + 2} d x + \int \frac{x}{x^{2} + 4} d x = - \int \frac{1}{x + 2} d x + \frac{1}{2} \int \frac{2 x}{x^{2} + 4} d x = - l n (x + 2) + \frac{1}{2} l n (x^{2} + 4) + c$

$15 \int \frac{x^{3} - 4 x^{2} - 2}{x^{3} + x^{2}} d x S o l u t i o n : \frac{x^{3} - 4 x^{2} - 2}{x^{3} + x^{2}} = \frac{2 - 5 x^{2}}{x^{3} + x^{2}} + 1 \frac{2 - 5 x^{2}}{x^{3} + x^{2}} = \frac{a}{x + 1} + \frac{b}{x} + \frac{c}{x^{2}} 2 - 5 x^{2} = a (x^{2}) + b (x + 1) (x) + c (x + 1) w h e n x = - 1 \Rightarrow - 3 = a \Rightarrow a = - 3 w h e n x = 0 \Rightarrow 2 = c \Rightarrow c = 2 w h e n x = 1 \Rightarrow - 3 = - 3 + 2 b + 4 \Rightarrow b = - 2 \int \frac{x^{3} - 4 x^{2} - 2}{x^{3} + x^{2}} d x = \int 1 d x - 3 \int \frac{1}{x + 1} d x - 2 \int \frac{1}{x} d x + 2 \int \frac{1}{x^{2}} d x = x - 3 l n (x + 1) - 2 l n (x) - \frac{2}{x} + c$

$16 \int \frac{3 - x}{2 - 5 x - 12 x^{2}} d x S o l u t i o n : \frac{3 - x}{2 - 5 x - 12 x^{2}} = \frac{a}{1 - 4 x} + \frac{b}{3 x + 2} 3 - x = a (3 x + 2) + b (1 - 4 x) w h e n x = \frac{1}{4} \Rightarrow \frac{11}{4} = \frac{11}{4} a \Rightarrow a = 1 w h e n x = - \frac{2}{3} \Rightarrow \frac{11}{3} = \frac{11}{3} b \Rightarrow b = 1 \int \frac{3 - x}{2 - 5 x - 12 x^{2}} d x = \int \frac{1}{1 - 4 x} d x + \int \frac{1}{3 x + 2} d x = - \frac{1}{4} \int \frac{- 4}{1 - 4 x} d x + \frac{1}{3} \int \frac{3}{3 x + 2} d x = - \frac{1}{4} l n (1 - 4 x) + \frac{1}{3} l n (3 x + 2) + c$

$17 \int \frac{3 x^{3} + 2 x^{2} + 12}{x^{4} + 6 x^{2}} d x S o l u t i o n : \frac{3 x^{3} + 2 x^{2} + 12}{x^{4} + 6 x^{2}} = \frac{3 x^{3}}{x^{2} (x^{2} + 6)} + \frac{2 (x^{2} + 6)}{x^{2} (x^{2} + 6)} = \frac{3 x}{x^{2} + 6} + \frac{2}{x^{2}} \int \frac{3 x^{3} + 2 x^{2} + 12}{x^{4} + 6 x^{2}} d x = \int (\frac{3 x}{x^{2} + 6} + x^{- 2}) d x = \frac{3}{2} \int \frac{2 x}{x^{2} + 6} d x + \int x^{- 2} d x = \frac{3}{2} \ln (x^{2} + 6) - x^{- 1} + c = \frac{3}{2} l n (x^{2} + 6) - \frac{1}{x} + c$

$18 \int \frac{5 x - 2}{{(x - 2)}^{2}} d x S o l u t i o n : \frac{5 x - 2}{{(x - 2)}^{2}} = \frac{5 x - 10 + 8}{{(x - 2)}^{2}} \frac{5 x - 2}{{(x - 2)}^{2}} = \frac{5 x - 10}{{(x - 2)}^{2}} + \frac{8}{{(x - 2)}^{2}} \frac{5 x - 2}{{(x - 2)}^{2}} = \frac{5 (x - 2)}{{(x - 2)}^{2}} + 8 {(x - 2)}^{- 2} \frac{5 x - 2}{{(x - 2)}^{2}} = \frac{5}{x - 2} + 8 {(x - 2)}^{- 2} \int \frac{5 x - 2}{{(x - 2)}^{2}} d x = \int \frac{5}{x - 2} d x + 8 \int {(x - 2)}^{- 2} d x = 5 l n (x - 2) - \frac{8}{x - 2} + c * * * w e c a n s o l v e i t a l s o b y p a r t i a l$

أجد كلاً من التكاملات الآتية:

$19 \int_{2}^{4} \frac{6 + 3 x - x^{2}}{x^{3} + 2 x^{2}} d x S o l u t i o n : \frac{6 + 3 x - x^{2}}{x^{3} + 2 x^{2}} = \frac{a}{x + 2} + \frac{b}{x} + \frac{c}{x^{2}} 6 + 3 x - x^{2} = a (x^{2}) + b (x + 2) (x) + c (x + 2) w h e n x = - 2 \Rightarrow - 4 = 4 a \Rightarrow a = - 1 w h e n x = 0 \Rightarrow 6 = 2 c \Rightarrow c = 3 w h e n x = 1 \Rightarrow 8 = - 1 + 3 b + 9 \Rightarrow b = 0 \int \frac{6 + 3 x - x^{2}}{x^{3} + 2 x^{2}} d x = - \int \frac{1}{x + 2} d x + \int \frac{0}{x} d x + 3 \int \frac{1}{x^{2}} d x = - l n (x + 2) + \frac{3}{x} \begin{array}{r} 4 \\ 2 \end{array}} = l n (\frac{2}{3}) + \frac{3}{4}$

$20 \int_{\frac{- 1}{3}}^{\frac{1}{3}} \frac{9 x^{2} + 4}{9 x^{2} - 4} d x S o l u t i o n : \frac{9 x^{2} + 4}{9 x^{2} - 4} = \frac{9 x^{2} - 4}{9 x^{2} - 4} + \frac{8}{9 x^{2} - 4} \frac{9 x^{2} + 4}{9 x^{2} - 4} = 1 + \frac{8}{9 x^{2} - 4} \frac{8}{9 x^{2} - 4} = \frac{a}{3 x + 2} + \frac{b}{3 x - 2} 8 = a (3 x - 2) + b (3 x + 2) w h e n x = - \frac{2}{3} \Rightarrow 8 = - 4 a \Rightarrow a = - 2 w h e n x = \frac{2}{3} \Rightarrow 8 = 4 b \Rightarrow b = 2 \int \frac{9 x^{2} + 4}{9 x^{2} - 4} d x = \int 1 d x + - 2 \int \frac{1}{3 x + 2} d x + 2 \int \frac{1}{3 x - 2} d x = \int 1 d x + - \frac{2}{3} \int \frac{3}{3 x + 2} d x + \frac{2}{3} \int \frac{3}{3 x - 2} d x \int_{\frac{- 1}{3}}^{\frac{1}{3}} \frac{9 x^{2} + 4}{9 x^{2} - 4} d x = x - \frac{2}{3} l n (3 x + 2) + \frac{2}{3} l n (3 x - 2) \begin{array}{r} \frac{1}{3} \\ \frac{- 1}{3} \end{array}} = \frac{2 - l n 81}{3} ≃ - 0.8$

$21 \int_{0}^{1} \frac{17 - 5 x}{(2 x + 3) {(2 - x)}^{2}} d x S o l u t i o n : \frac{17 - 5 x}{(2 x + 3) {(2 - x)}^{2}} = \frac{a}{2 x + 3} + \frac{b}{2 - x} + \frac{c}{{(2 - x)}^{2}} 17 - 5 x = a {(2 - x)}^{2} + b (2 x + 3) (2 - x) + c (2 x + 3) w h e n x = - \frac{3}{2} \Rightarrow \frac{49}{2} = \frac{49}{4} a \Rightarrow a = 2 w h e n x = 2 \Rightarrow 7 = 7 c \Rightarrow c = 1 w h e n x = 0 \Rightarrow 17 = 8 + 6 b + 3 \Rightarrow b = 1 \int \frac{17 - 5 x}{(2 x + 3) {(2 - x)}^{2}} d x = \int \frac{2}{2 x + 3} d x + \int \frac{1}{2 - x} d x + \int \frac{1}{{(2 - x)}^{2}} d x = l n (2 x + 3) - l n (2 - x) + \frac{1}{2 - x} 1 0 = \frac{\ln 25 - \ln 9 + \ln 4 + 1}{2} ≃ 1.7$

$22 \int_{1}^{4} \frac{4}{16 x^{2} + 8 x - 3} d x S o l u t i o n : \frac{4}{16 x^{2} + 8 x - 3} = \frac{a}{4 x - 1} + \frac{b}{4 x + 3} 4 = a (4 x + 3) + b (4 x - 1) w h e n x = \frac{1}{4} \Rightarrow 4 = 4 a \Rightarrow a = 1 w h e n x = - \frac{3}{4} \Rightarrow 4 = - 4 b \Rightarrow b = - 1 \int \frac{4}{16 x^{2} + 8 x - 3} d x = \int \frac{1}{4 x - 1} d x - \int \frac{1}{4 x + 3} d x = \frac{1}{4} \int \frac{4}{4 x - 1} d x - \frac{1}{4} \int \frac{4}{4 x + 3} d x \int_{1}^{4} \frac{4}{16 x^{2} + 8 x - 3} d x = \frac{1}{4} l n (4 x - 1) - \frac{1}{4} l n (4 x + 3) 4 1 = \frac{- l n 19 + l n 15 + l n 7 - l n 3}{4} ≃ 0.15$

$23 \int_{3}^{4} \frac{5 x + 5}{x^{2} + x - 6} d x S o l u t i o n : \frac{5 x + 5}{x^{2} + x - 6} = \frac{a}{x + 3} + \frac{b}{x - 2} 5 x + 5 = a (x - 2) + b (x + 3) w h e n x = - 3 \Rightarrow - 10 = - 5 a \Rightarrow a = 2 w h e n x = 2 \Rightarrow 15 = 5 b \Rightarrow b = 3 \int \frac{5 x + 5}{x^{2} + x - 6} d x = 2 \int \frac{1}{x + 3} d x + 3 \int \frac{1}{x - 2} d x \int_{3}^{4} \frac{5 x + 5}{x^{2} + x - 6} d x = 2 \int \frac{1}{x + 3} d x + 3 \int \frac{1}{x - 2} d x = 2 l n (x + 3) + 3 l n (x - 2) \begin{array}{r} 4 \\ 3 \end{array}} = 2 l n 7 - 2 l n 6 + 3 l n 2 ≃ 2.39$

$24 \int_{3}^{4} \frac{4}{x^{3} - 4 x^{2} + 4 x} d x S o l u t i o n : \frac{4}{x^{3} - 4 x^{2} + 4 x} = \frac{4}{x {(x - 2)}^{2}} = \frac{a}{x} + \frac{b}{x - 2} + \frac{c}{{(x - 2)}^{2}} 4 = a {(x - 2)}^{2} + b x (x - 2) + c x w h e n x = 0 \Rightarrow 4 = 4 a \Rightarrow a = 1 w h e n x = 2 \Rightarrow 4 = 2 c \Rightarrow c = 2 w h e n x = 1 \Rightarrow 4 = 1 + - b + 2 \Rightarrow b = - 1 \int \frac{4}{x^{3} - 4 x^{2} + 4 x} d x = \int \frac{1}{x} d x - \int \frac{1}{x - 2} d x + 2 \int \frac{1}{{(x - 2)}^{2}} d x \int_{3}^{4} \frac{4}{x^{3} - 4 x^{2} + 4 x} d x = l n (x) - l n (x - 2) - \frac{2}{x - 2} \begin{array}{r} 4 \\ 3 \end{array}} = l n 4 - l n 3 - l n 2 + 1 ≃ 0.59$

أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين :

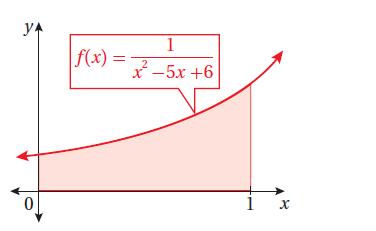
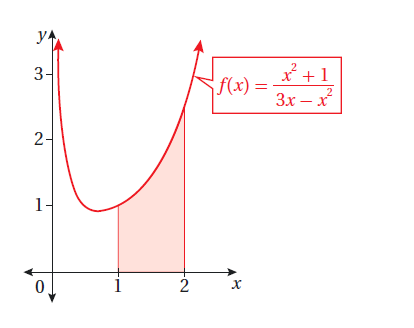
$25 \int_{0}^{1} \frac{1}{x^{2} - 5 x + 6} d x S o l u t i o n : \frac{1}{x^{2} - 5 x + 6} = \frac{a}{x - 3} + \frac{b}{x - 2} 1 = a (x - 2) + b (x - 3) w h e n x = 3 \Rightarrow 1 = a \Rightarrow a = 1 w h e n x = 2 \Rightarrow 1 = - b \Rightarrow b = - 1 \int \frac{1}{x^{2} - 5 x + 6} d x = \int \frac{1}{x - 3} d x - \int \frac{1}{x - 2} d x \int_{0}^{1} \frac{1}{x^{2} - 5 x + 6} d x = l n (x - 3) - l n (| x - 2 |) \begin{array}{r} 1 \\ 0 \end{array}} = 2 l n 2 - l n 3 ≃ 0.29$

$26 \int_{1}^{2} \frac{x^{2} + 1}{3 x - x^{2}} d x S o l u t i o n : \frac{x^{2} + 1}{3 x - x^{2}} = \frac{x^{2} - 3 x + 3 x - 1}{3 x - x^{2}} \frac{x^{2} + 1}{3 x - x^{2}} = \frac{x^{2} - 3 x}{3 x - x^{2}} + \frac{3 x + 1}{3 x - x^{2}} \frac{x^{2} + 1}{3 x - x^{2}} = - 1 + \frac{a}{3 - x} + \frac{b}{x} 3 x + 1 = a (x) + b (3 - x) w h e n x = 3 \Rightarrow 10 = 3 a \Rightarrow a = \frac{10}{3} w h e n x = 0 \Rightarrow 1 = 3 b \Rightarrow b = \frac{1}{3} \int \frac{x^{2} + 1}{3 x - x^{2}} d x = \int - 1 d x + \frac{10}{3} \int \frac{1}{3 - x} d x + \frac{1}{3} \int \frac{1}{x} d x \int_{1}^{2} \frac{x^{2} + 1}{3 x - x^{2}} d x = - x - \frac{10}{3} l n (3 - x) + \frac{1}{3} l n (x) \begin{array}{r} 2 \\ 1 \end{array}} = \frac{11 l n 3}{2} - 1 ≃ 1.54$

يبين الشكل المجاور جزءا من منحنى الاقتران 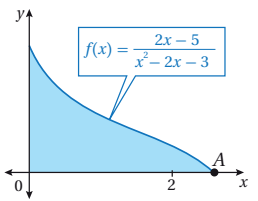$f (x) = \frac{2 x - 5}{x^{2} - 2 x - 3}$ :

$27$ أجد إحداثيي النقطة A .

$S o l u t i o n : f (x) = \frac{2 x - 5}{x^{2} - 2 x - 3} = 0 2 x - 5 = 0 \Rightarrow x = \frac{5}{2}$

$28$ أجد مساحة المنطقة المظللة .

$S o l u t i o n : A = \int_{0}^{\frac{5}{2}} \frac{2 x - 5}{x^{2} - 2 x - 3} d x \int_{0}^{\frac{5}{2}} \frac{2 x - 5}{x^{2} - 2 x - 3} d x = \int_{0}^{\frac{5}{2}} \frac{2 x - 2}{x^{2} - 2 x - 3} d x - \int_{0}^{\frac{5}{2}} \frac{3}{x^{2} - 2 x - 3} d x \int_{0}^{\frac{5}{2}} \frac{3}{x^{2} - 2 x - 3} d x = ? \frac{3}{x^{2} - 2 x - 3} = \frac{A}{x - 3} + \frac{B}{x + 1} A (x + 1) + B (x - 3) = 3 w h e n x = - 1 \Rightarrow B = - \frac{3}{4} w h e n x = 3 \Rightarrow A = \frac{3}{4} \int_{0}^{\frac{5}{2}} \frac{2 x - 5}{x^{2} - 2 x - 3} d x = \int_{0}^{\frac{5}{2}} \frac{2 x - 2}{x^{2} - 2 x - 3} d x - \int_{0}^{\frac{5}{2}} \frac{3}{x^{2} - 2 x - 3} d x = \ln (x^{2} - 2 x - 3) \frac{5}{2} 0 - \frac{3}{4} \ln (x + 3) \frac{5}{2} 0 + \frac{3}{4} \ln (x - 1) \frac{5}{2} 0 = (\ln (\frac{25}{4} - 5 - 3) - \ln (- 3)) - \frac{3}{4} (\ln (\frac{5}{2} + 3) - \ln (0 + 3)) + \frac{3}{4} (\ln (\frac{5}{2} - 1) - l n (0 - 1)) = (l n (\frac{7}{4}) - l n (3)) - \frac{3}{4} (l n (\frac{11}{2}) - l n (3)) + \frac{3}{4} (l n (\frac{3}{2}))$

أجد كلاً من التكاملات الآتية:

$29 \int \frac{\sin x}{\cos x + \cos^{2} x} d x S o l u t i o n : l e t u = \cos x \Rightarrow d x = - \frac{d u}{\sin x} \int \frac{s i n x}{c o s x + c o s^{2} x} d x = - \int \frac{\sin x}{u + u^{2}} \frac{d u}{\sin x} = \int \frac{- 1}{u + u^{2}} d u \frac{- 1}{u + u^{2}} = \frac{A}{u} + \frac{B}{u + 1} - 1 = A (u + 1) + B (u) w h e n u = 0 \Rightarrow - 1 = A \Rightarrow A = - 1 w h e n u = - 1 \Rightarrow - 1 = - B \Rightarrow B = 1 \int \frac{- 1}{u + u^{2}} d u = - \int \frac{1}{u} d u + \int \frac{1}{u + 1} d u = - l n (u) + l n (u + 1) = - l n (c o s x) + l n (c o s x + 1) + c$

$30 \int \frac{1}{x^{2} + x \sqrt{x}} d x S o l u t i o n : l e t u = \sqrt{x} \Rightarrow d x = 2 \sqrt{x} d u u^{2} = x, u^{4} = x^{2} \int \frac{1}{x^{2} + x \sqrt{x}} d x = \int \frac{1}{u^{4} + u^{3}} 2 u d u = \int \frac{2}{u^{3} + u^{2}} d u \frac{2}{u^{3} + u^{2}} = \frac{a}{u + 1} + \frac{b}{u} + \frac{c}{u^{2}} 2 = a u^{2} + b u (u + 1) + c (u + 1) w h e n u = 0 \Rightarrow 2 = c \Rightarrow c = 2 w h e n u = - 1 \Rightarrow 2 = a \Rightarrow a = 2 w h e n u = 1 \Rightarrow 2 = 2 + 2 b + 4 \Rightarrow b = - 2 \int \frac{2}{u^{3} + u^{2}} d u = 2 \int \frac{1}{u + 1} d u - 2 \int \frac{1}{u} d u + 2 \int \frac{1}{u^{2}} d u = 2 l n (u + 1) - 2 l n (u) - \frac{2}{u} = 2 l n (\sqrt{x} + 1) - 2 l n (\sqrt{x}) - \frac{2}{\sqrt{x}} + c = 2 l n (\sqrt{x} + 1) - l n (x) - \frac{2}{\sqrt{x}} + c$

$31 \int \frac{e^{2 x}}{e^{2 x} + 3 e^{x} + 2} d x S o l u t i o n : l e t u = e^{x} \Rightarrow d x = \frac{d u}{e^{x}} \int \frac{e^{2 x}}{e^{2 x} + 3 e^{x} + 2} d x = \int \frac{e^{2 x}}{u^{2} + 3 u + 2} \frac{d u}{e^{x}} = \int \frac{u}{u^{2} + 3 u + 2} d u \frac{u}{u^{2} + 3 u + 2} = \frac{a}{u + 1} + \frac{b}{u + 2} u = a (u + 2) + b (u + 1) w h e n u = - 1 \Rightarrow - 1 = a \Rightarrow a = - 1 w h e n u = - 2 \Rightarrow - 2 = - b \Rightarrow b = 2 \int \frac{u}{u^{2} + 3 u + 2} d u = - \int \frac{1}{u + 1} d u + 2 \int \frac{1}{u + 2} d u = - l n (u + 1) + 2 l n (u + 2) = - l n (e^{x} + 1) + 2 l n (e^{x} + 2) + c$

$32 \int \frac{c o s x}{(s i n^{2} x - 4) s i n x} d x S o l u t i o n : l e t u = s i n x \Rightarrow d x = \frac{d u}{c o s x} \int \frac{c o s x}{(s i n^{2} x - 4) s i n x} d x = - \int \frac{c o s x}{(u^{2} - 4) u} \frac{d u}{c o s x} = \int \frac{1}{(u^{2} - 4) u} d u \frac{1}{(u^{2} - 4) u} = \frac{a}{u} + \frac{b}{u - 2} + \frac{c}{u + 2} 1 = a (u - 1) (u + 2) + b (u) (u + 2) + c (u) (u - 2) w h e n u = 0 \Rightarrow 1 = - 2 a \Rightarrow a = - \frac{1}{2} w h e n u = 2 \Rightarrow 1 = - 2 + 8 b \Rightarrow b = \frac{3}{8} w h e n u = - 2 \Rightarrow 1 = 8 c \Rightarrow c = \frac{1}{8} \int \frac{1}{(u^{2} - 4) u} d u = - \frac{1}{2} \int \frac{1}{u} d u + \frac{3}{8} \int \frac{1}{u - 2} d u + \frac{1}{8} \int \frac{1}{u + 2} d u = - \frac{1}{2} l n (u) + \frac{3}{8} l n (u - 2) + \frac{1}{8} l n (u + 2) = - \frac{1}{2} l n (s i n x) + \frac{3}{8} l n (s i n x - 2) + \frac{1}{8} l n (s i n x + 2) + c$

$33$ أجد $\int \frac{1}{1 + e^{x}} d x$ بطريقتين مختلفتين إحداهما الكسور الجزئية ، مبرراً أجابتي :

$S o l u t i o n 1 : \int \frac{1}{1 + e^{x}} d x = \int \frac{1}{1 + e^{x}} \times \frac{e^{- x}}{e^{- x}} d x = \int \frac{e^{- x}}{e^{- x} + 1} d x = - \ln (e^{- x} + 1) + c = - l n (\frac{1}{e^{x}} + 1) + c = - l n (\frac{1 + e^{x}}{e^{x}}) + c = l n (\frac{e^{x}}{1 + e^{x}}) + c S o l u t i o n 2 : l e t u = e^{x} \Rightarrow d x = \frac{d u}{e^{x}} \int \frac{1}{1 + e^{x}} d x = \int \frac{1}{1 + u} \frac{d u}{u} = \int \frac{1}{(u^{2} + u)} d u \frac{1}{(u^{2} + u)} = \frac{a}{u} + \frac{b}{u + 1} 1 = a (u + 1) + b (u) w h e n u = 0 \Rightarrow 1 = a \Rightarrow a = 1 w h e n u = - 1 \Rightarrow 1 = - b \Rightarrow b = - 1 \int \frac{1}{(u^{2} + u)} d u = \int \frac{1}{u} d u - \int \frac{1}{u + 1} d u = l n (u) - l n (u + 1) = l n (\frac{u}{u + 1}) = l n (\frac{e^{x}}{e^{x} + 1}) + c$

$34 \int_{0}^{l n 2} \frac{1}{1 + e^{x}} d x S o l u t i o n : \int_{0}^{l n 2} \frac{1}{1 + e^{x}} d x = l n (\frac{e^{x}}{1 + e^{x}}) \begin{array}{r} l n 2 \\ 0 \end{array}} = l n (\frac{e^{l n 2}}{1 + e^{l n 2}}) - l n (\frac{e^{0}}{1 + e^{0}}) = l n (\frac{2}{3}) - l n (\frac{1}{2}) = l n (\frac{4}{3})$

$35$ أثبت أن : $\int_{4}^{9} \frac{5 x^{2} - 8 x + 1}{2 x {(x - 1)}^{2}} d x = l n (\frac{32}{3}) - \frac{5}{24}$

$S o l u t i o n : \frac{5 x^{2} - 8 x + 1}{2 x {(x - 1)}^{2}} = \frac{a}{2 x} + \frac{b}{x - 1} + \frac{c}{{(x - 1)}^{2}} 5 x^{2} - 8 x + 1 = a {(x - 1)}^{2} + 2 b x (x - 1) + 2 c x w h e n x = 0 \Rightarrow 1 = a \Rightarrow a = 1 w h e n x = 1 \Rightarrow - 2 = 2 c \Rightarrow c = - 1 w h e n x = 2 \Rightarrow 5 = 1 + 4 b + - 4 \Rightarrow b = 2 \int \frac{5 x^{2} - 8 x + 1}{2 x {(x - 1)}^{2}} d x = \frac{1}{2} \int \frac{1}{x} d x + 2 \int \frac{1}{x - 1} d x - \int \frac{1}{{(x - 1)}^{2}} d x \int_{4}^{9} \frac{5 x^{2} - 8 x + 1}{2 x {(x - 1)}^{2}} d x = \frac{1}{2} l n (x) + 2 l n (x - 1) + \frac{1}{x - 1} \begin{array}{r} 9 \\ 4 \end{array}} = (\frac{1}{2} \ln (9) + 2 \ln (9 - 1) + \frac{1}{9 - 1}) - (\frac{1}{2} l n (4) + 2 l n (4 - 1) + \frac{1}{4 - 1}) = (l n (3) + l n (64) + \frac{1}{8}) - (l n (2) + l n (9) + \frac{1}{3}) = l n (3 \times 64) + \frac{1}{8} - \ln (2 \times 9) - \frac{1}{3} = l n (\frac{3 \times 64}{2 \times 9}) - \frac{5}{24} = l n (\frac{32}{3}) - \frac{5}{24}$

$36$ أثبت أن : $\int_{9}^{16} \frac{2 \sqrt{x}}{x - 4} d x = 4 (1 + l n (\frac{5}{3}))$

$S o l u t i o n : l e t u = \sqrt{x} u^{2} = x \Rightarrow d x = 2 u d u \int \frac{2 \sqrt{x}}{x - 4} d x = \int \frac{2 u}{u^{2} - 4} 2 u d u = \int \frac{4 u^{2}}{u^{2} - 4} d u = \int \frac{4 u^{2} - 16}{u^{2} - 4} d u + \int \frac{16}{u^{2} - 4} d u \int \frac{4 u^{2}}{u^{2} - 4} d u = \int 4 d u + \int \frac{16}{u^{2} - 4} d u \frac{16}{u^{2} - 4} = \frac{a}{u - 2} + \frac{b}{u + 2} 16 = a (u + 2) + b (u - 2) w h e n u = 2 \Rightarrow 16 = 4 a \Rightarrow a = 4 w h e n u = - 2 \Rightarrow 16 = - 4 b \Rightarrow b = - 4 \int_{3}^{4} \frac{16}{u^{2} - 4} d u = 4 \int \frac{1}{u - 2} d u - 4 \int \frac{1}{u + 2} d u = 4 l n (u - 2) - 4 l n (u + 2) 4 3 = 4 (l n (u - 2) - l n (u + 2)) 4 3 = 4 l n (\frac{u - 2}{u + 2}) 4 3 = 4 (l n (\frac{1}{3}) - l n (\frac{1}{5})) = 4 l n (\frac{1}{3} \times \frac{5}{1}) = 4 l n (\frac{5}{3}) \int_{3}^{4} \frac{4 u^{2}}{u^{2} - 4} d u = \int_{3}^{4} 4 d u + \int_{3}^{4} \frac{16}{u^{2} - 4} d u = 4 + 4 l n (\frac{5}{3}) = 4 (1 + l n (\frac{5}{3}))$

$37$ أثبت أن : $\int_{0}^{1} \frac{4 x^{2} + 9 x + 4}{2 x^{2} + 5 x + 3} d x = 2 + \frac{1}{2} l n (\frac{5}{12})$

$\int_{0}^{1} \frac{4 x^{2} + 9 x + 4}{2 x^{2} + 5 x + 3} d x S o l u t i o n : \frac{4 x^{2} + 9 x + 4}{2 x^{2} + 5 x + 3} = \frac{4 x^{2} + 10 x + 6}{2 x^{2} + 5 x + 3} - \frac{x + 2}{2 x^{2} + 5 x + 3} \frac{4 x^{2} + 9 x + 4}{2 x^{2} + 5 x + 3} = 2 \frac{2 x^{2} + 5 x + 3}{2 x^{2} + 5 x + 3} - \frac{x + 2}{2 x^{2} + 5 x + 3} \frac{4 x^{2} + 9 x + 4}{2 x^{2} + 5 x + 3} = 2 - \frac{x + 2}{2 x^{2} + 5 x + 3} \int \frac{x + 2}{2 x^{2} + 5 x + 3} d x = \frac{x + 2}{2 x^{2} + 5 x + 3} = \frac{a}{2 x + 3} + \frac{b}{x + 1} x + 2 = a (x + 1) + b (2 x + 3) w h e n x = - \frac{3}{2} \Rightarrow \frac{1}{2} = - \frac{1}{2} a \Rightarrow a = - 1 w h e n x = - 1 \Rightarrow 1 = b \Rightarrow b = 1 \int \frac{x + 2}{2 x^{2} + 5 x + 3} d x = - \int \frac{1}{2 x + 3} d x + \int \frac{1}{x + 1} d x = - \frac{1}{2} l n (2 x + 3) + l n (x + 1) 1 0 = (- \frac{1}{2} \ln (5) + \frac{1}{2} l n (3)) + (l n (2) - l n (1)) = - \frac{1}{2} l n (\frac{5}{3}) + l n (2) \int_{0}^{1} \frac{4 x^{2} + 9 x + 4}{2 x^{2} + 5 x + 3} d x = 2 x 1 0 - (- \frac{1}{2} l n (\frac{5}{3}) + l n (2)) = 2 + \frac{1}{2} l n (\frac{5}{3}) - l n (2) = 2 + \frac{1}{2} (\ln (\frac{5}{3}) - \ln (4)) = 2 + \frac{1}{2} l n (\frac{5}{12})$

$38 \int \frac{\sqrt{1 + \sqrt{x}}}{x} d x S o l u t i o n : l e t u = 1 + \sqrt{x} \Rightarrow d x = 2 \sqrt{x} d u \int \frac{\sqrt{1 + \sqrt{x}}}{x} d x = \int \frac{\sqrt{u}}{x} 2 \sqrt{x} d u = 2 \int \frac{\sqrt{u}}{\sqrt{x}} d u = 2 \int \frac{\sqrt{u}}{u - 1} d u l e t w = \sqrt{u} \Rightarrow d u = 2 w d w 2 \int \frac{\sqrt{u}}{u - 1} d u = 2 \int \frac{w}{w^{2} - 1} 2 w d w = 4 \int \frac{w^{2}}{w^{2} - 1} d w = 4 \int \frac{w^{2} - 1}{w^{2} - 1} d w + 4 \int \frac{1}{w^{2} - 1} d w = 4 \int d w + 4 \int \frac{1}{w^{2} - 1} d w \frac{4}{w^{2} - 1} = \frac{a}{w - 1} + \frac{b}{w + 1} 4 = a (w + 1) + b (w - 1) w h e n w = 1 \Rightarrow 4 = 2 a \Rightarrow a = 2 w h e n w = - 1 \Rightarrow 4 = - 2 b \Rightarrow b = - 2 \int \frac{4}{w^{2} - 1} d u = 2 \int \frac{1}{w - 1} d u - 2 \int \frac{1}{w + 1} d u = 2 l n (w - 1) - 2 l n (w + 1) = 2 l n (\sqrt{u} - 1) - 2 l n (\sqrt{u} + 1) = 2 l n (\sqrt{1 + \sqrt{x}} - 1) - 2 l n (\sqrt{1 + \sqrt{x}} + 1) = 2 l n (\frac{\sqrt{1 + \sqrt{x}} - 1}{\sqrt{1 + \sqrt{x}} + 1}) \int \frac{\sqrt{1 + \sqrt{x}}}{x} d x = 4 (\sqrt{1 + \sqrt{x}}) + 2 l n (\frac{\sqrt{1 + \sqrt{x}} - 1}{\sqrt{1 + \sqrt{x}} + 1}) + c$

$39 \int \frac{x}{16 x^{4} - 1} d x S o l u t i o n : l e t u = x^{2} \Rightarrow d x = \frac{d u}{2 x} \int \frac{x}{16 x^{4} - 1} d x = \int \frac{x}{16 u^{2} - 1} \frac{d u}{2 x} = \frac{1}{2} \int \frac{1}{16 u^{2} - 1} d u \frac{1}{16 u^{2} - 1} = \frac{a}{4 u - 1} + \frac{b}{4 u + 1} 1 = a (4 u + 1) + b (4 u - 1) w h e n u = \frac{1}{4} \Rightarrow 1 = 2 a \Rightarrow a = \frac{1}{2} w h e n u = 0 \Rightarrow 1 = - 2 b \Rightarrow b = - \frac{1}{2} \frac{1}{2} \int \frac{1}{16 u^{2} - 1} d u = \frac{1}{4} \int \frac{1}{4 u - 1} d u - \frac{1}{4} \int \frac{1}{4 u + 1} d u = \frac{1}{16} \int \frac{4}{4 u - 1} d u - \frac{1}{16} \int \frac{4}{4 u + 1} d u = \frac{1}{16} l n (4 u - 1) - \frac{1}{16} l n (4 u + 1) = \frac{1}{16} l n (4 x^{2} - 1) - \frac{1}{16} l n (4 x^{2} + 1) + c$

رياضيات فصل ثاني

التوجيهي علمي

Get it for

MAC

Get it for

WINDOWS