رياضيات

المنحنى الطبيعي: هو منحنى تكراري يستخدم لنمذجة البيانات العددية المتصلة التي يتم اختيارها عشوائيًا في مواقف حياتية مختلفة بحيث يكون عدد البيانات كبير جدًا والذي يمتاز بما يلي:

منحنى متصل له شكل الجرس

تطابق الوسط الحسابي والوسيط والمنوال, ويتوسط البيانات.

تماثل البيانات حول الوسط الحسابي.

اقتراب المنحنى عند طرفيه من المحور الأفقي x دون أن يمسّه.

المساحة الكلية أسفل المنحنى الطبيعي المعياري هي 1. 

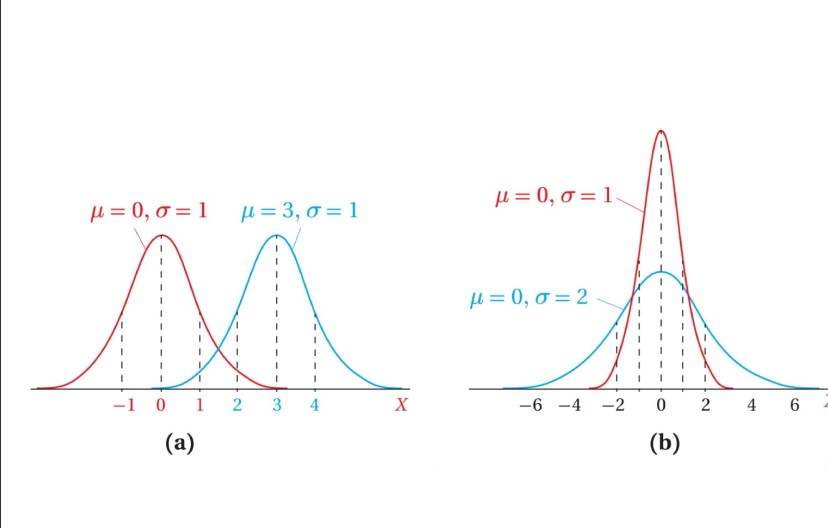
ويعتمد المنحنى الطبيعي على قيمة كل من الوسط الحسابي ($\mu$) والانحراف المعياري ($\sigma$), حيث:

1)زيادة الوسط الحسابي, تؤدي إلى انسحاب أفقي نحو اليمين

2)زيادة الانحراف المعياري تؤدي إلى زيادة انتشار وتوسع المنحنى.

لاحظ الشكل التالي:

القاعدة التجريبية:

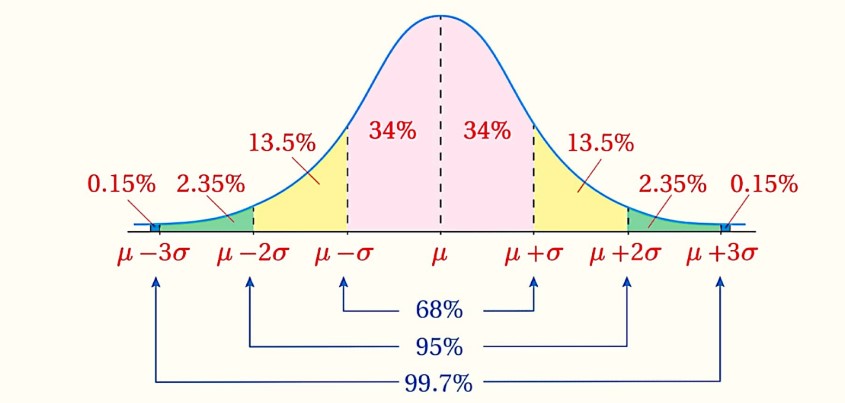
إذا اتخذت مجموعة من البيانات شكل المنحنى الطبيعي بوسط حسابي $\mu$ وانحراف معياري $\sigma$ فإنه ما يقارب:

1)%68 من البيانات تقع بين $\mu +\sigma و \mu -\sigma$

(لا يزيد البعد بينها وبين الوسط الحسابي عن انحراف معياري واحد)

2)95% من البيانات تقع بين $\mu +2\sigma و \mu -2\sigma$ (لا يزيد البعد بينها وبين الوسط الحسابي عن انحرافين معياريين) 

3) 99.7% من البيانات تقع بين $\mu +3\sigma و \mu -3\sigma$ (لا يزيد البعد بينها وبين الوسط الحسابي عن ثلاثة انحرافات معيارية)

ويمكن تلخيص القاعدة التجريبية بالشكل التالي:

مثال1: إذا اتخذت كتل مجموعة من طلبة الصف التاسع شكل المنحنى الطبيعي, فجد كلًا مما يلي:

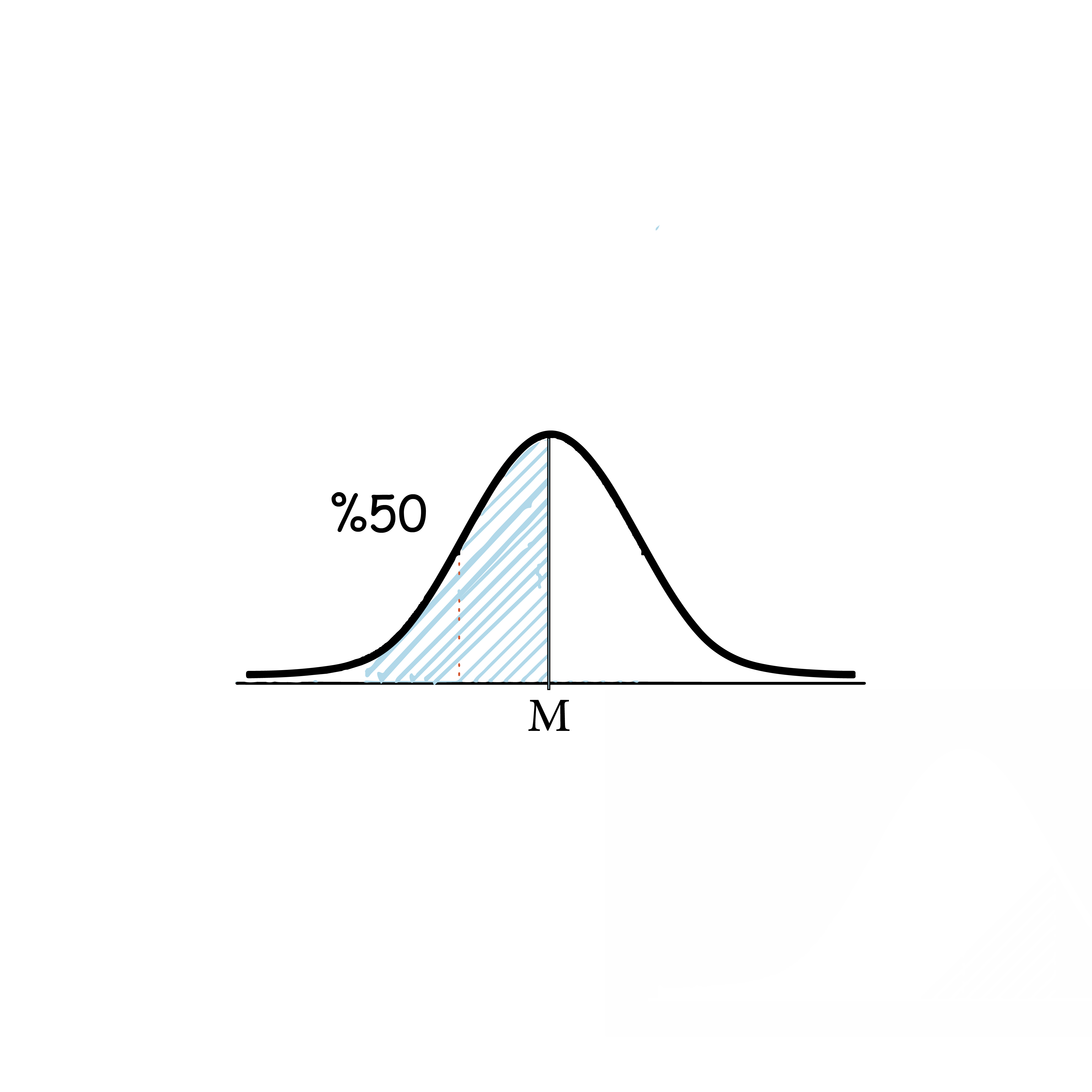
1)النسبة المئوية للطلبة الذين تقل كتلتهم عن الوسط الحسابي.

الحل: بسبب التماثل حول الوسط الحسابي, فإن 50% من الطلبة تقل كتلهم عن الوسط الحسابي.

2)النسبة المئوية للطلبة الذين تزيد كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحراف معياري واحد.

الحل: لاحظ الشكل المجاور:

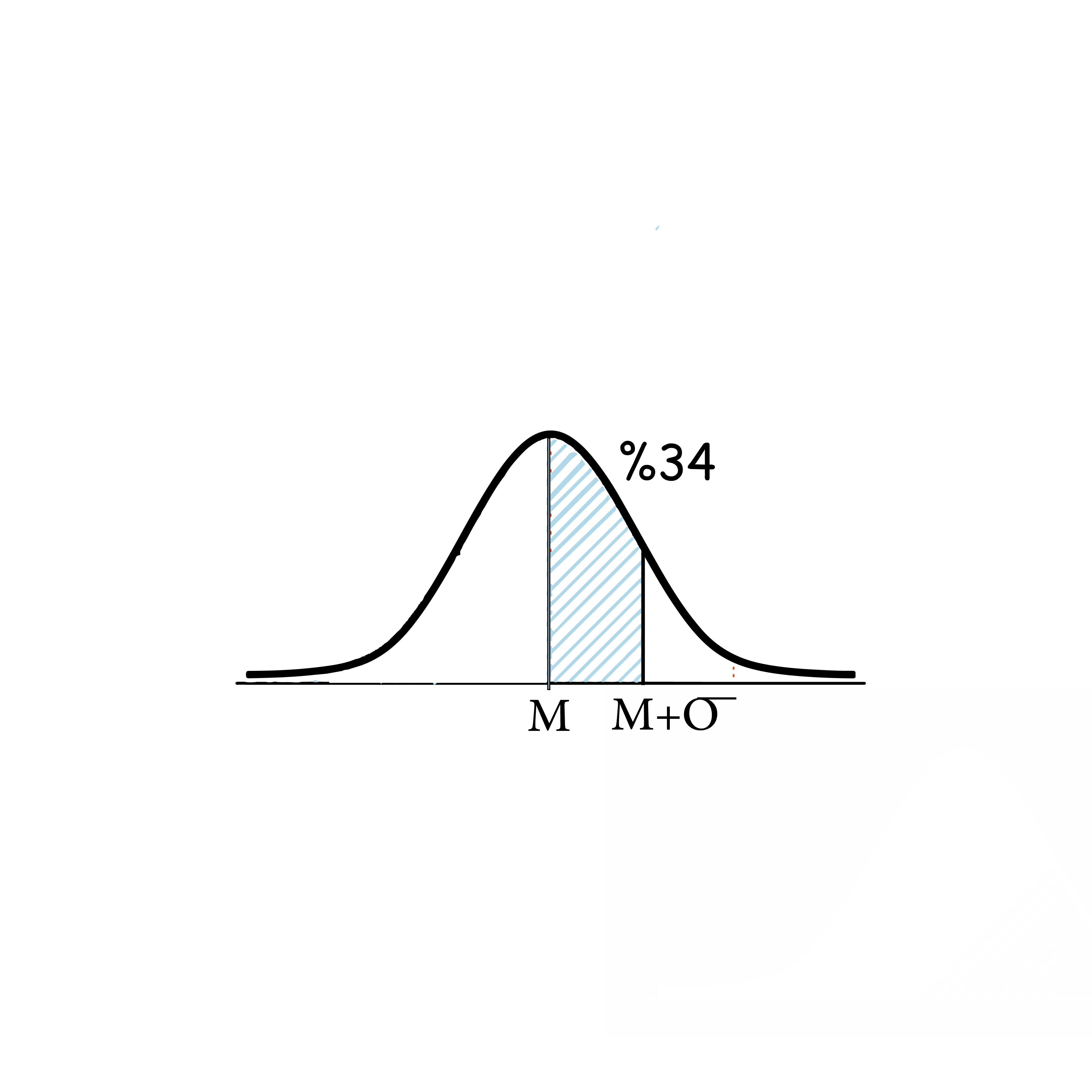
34% من الطلبة تزيد كتلهم عن الوسط الحسابي بما لا يزيد عن انحراف معياري واحد.

3)نسبة الطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين, أو تزيد عليه بمقدار لا يزيد عن ثلاثة انحرافات معيارية.

الحل: لاحظ الشكل المجاور:

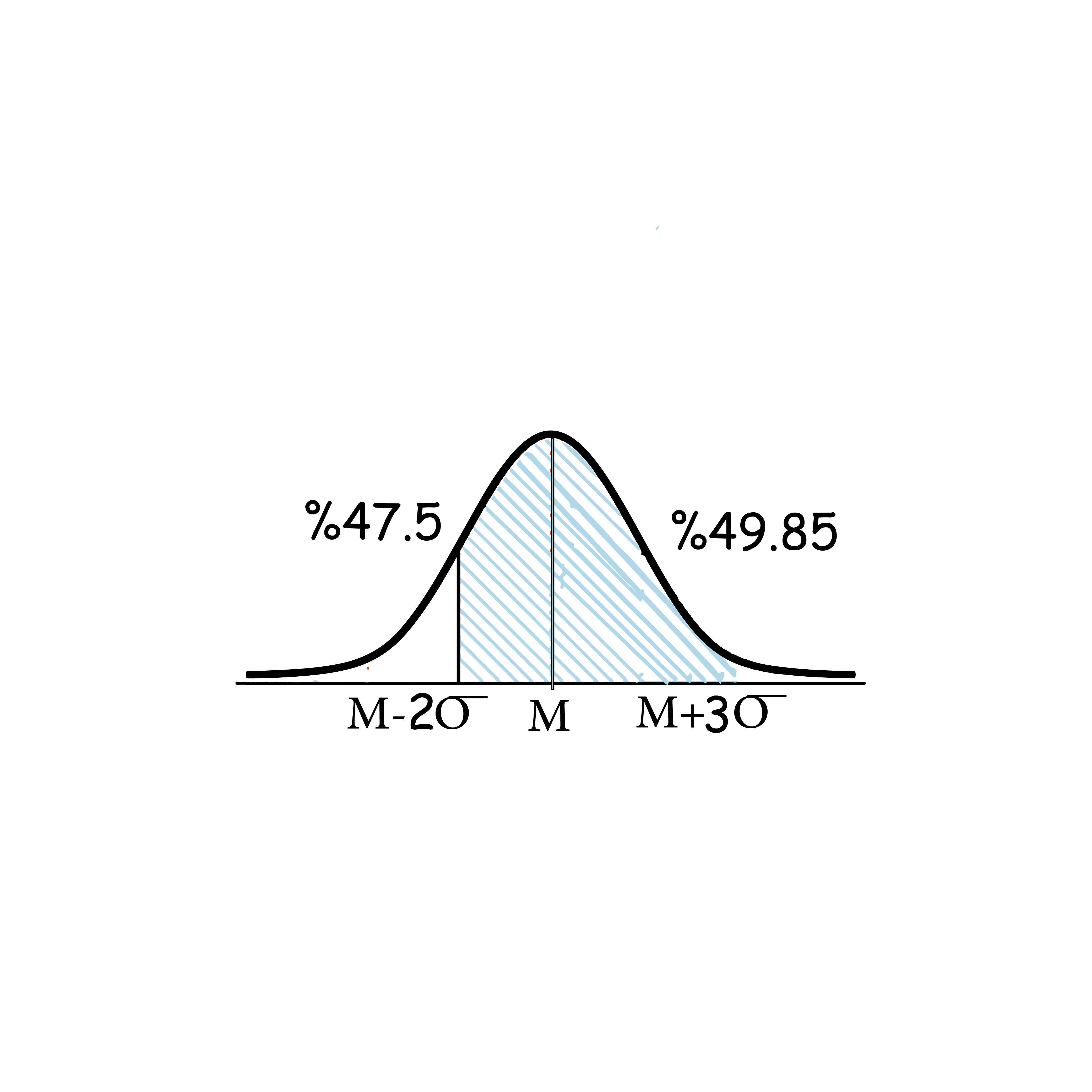
النسبة هي: (47.5+49.85)%

97.35%

4)النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي بمقدار لا يقل عن انحراف معياري واحد:

الحل: لاحظ الشكل المجاور:

النسبة هي:(50-34)%

16%

المتغير العشوائي الطبيعي, والتوزيع الطبيعي:

1)المتغير العشوائي المنفصل: هو متغير عشوائي يأخذ قيمًا معدودة ومن الأمثلة عليه:

المتغير العشوائي الهندسي, والمتغير العشوائي ذي الحدين

مثل: عدد الأشجار التي ستنمو عند زراعة 10000 شجرة.

2)المتغير العشوائي المتصل: هو متغير عشوائي يأخذ قيمًا متصلة ضمن فترة معينة من الأعداد الحقيقية ومن الأمثلة عليه: التوزيع الطبيعي.

مثل: طول الشجرة يتم اختيارها عشوائيًا من أشجار غابة ما.

فالتوزيع الطبيعي: هو التوزيع الاحتمالي للمتغير العشوائي المتصل X الذي يتخذ تمثيله البياني شكل المنحنى الطبيعي, ويسمى هذا المتغير العشوائي: متغيرًا عشوائيًا طبيعيًا ويرمز له بالرمز:

$X~N(\mu ,{\sigma }^2)$

حيث:

$\mu$: الوسط الحسابي

$\sigma$: الانحراف المعياري

${\sigma }^2$: التباين

ويمكن استخدام القاعدة التجريبية لإيجاد احتمال حادث معين لمتغير عشوائي طبيعي, والتي تمثل النسبة المئوية للمساحة تحت المنحنى.

مثال2: يدل المتغير العشوائي X على سعة علبة عصير (بالميلمتر) ينتجه مصنع معين, حيث:

X~N(250,3²)

فجد كلًا مما يلي:

1)P(X<250)

الحل: بسبب التماثل حول الوسط الحسابي:

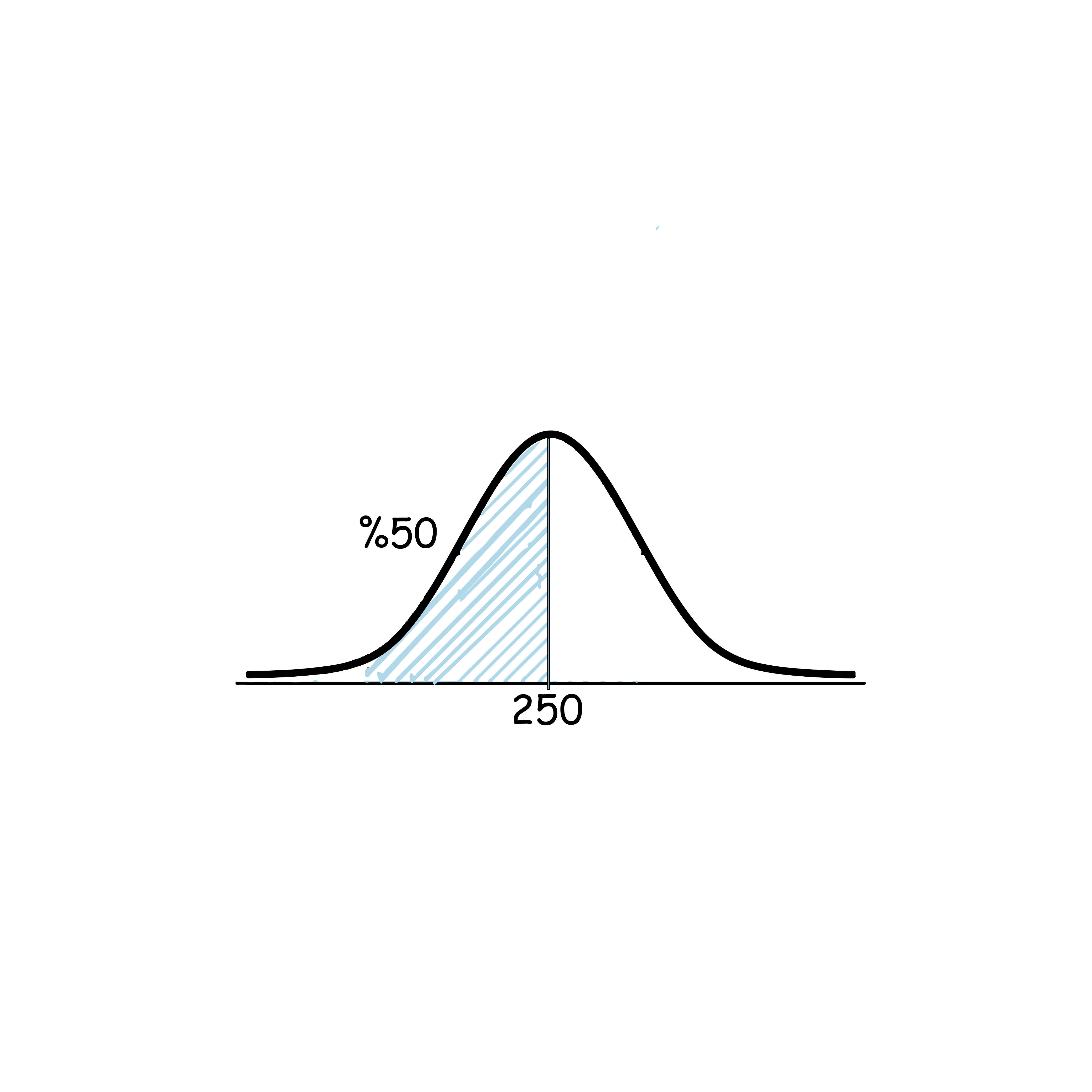
P(X<250)=0.5

2)P(247>X>265)

الحل:

$$\begin{gathered} 247=250-3=\mu -\sigma \\ 265=250+6=\mu +2\sigma \end{gathered}$$

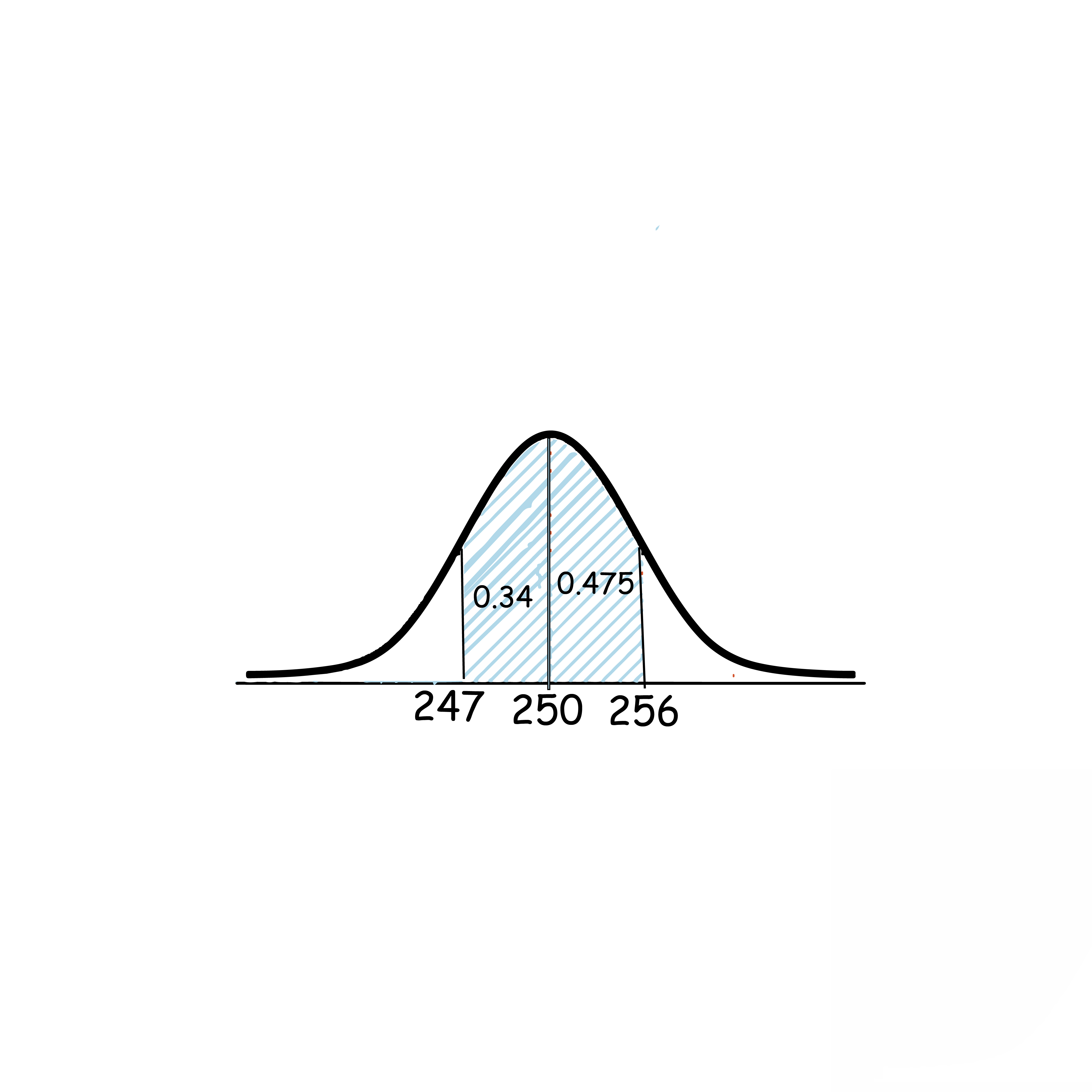
P(247<X<256)=0.34+.475

                        =0.815

3)P(X<244)

الحل:

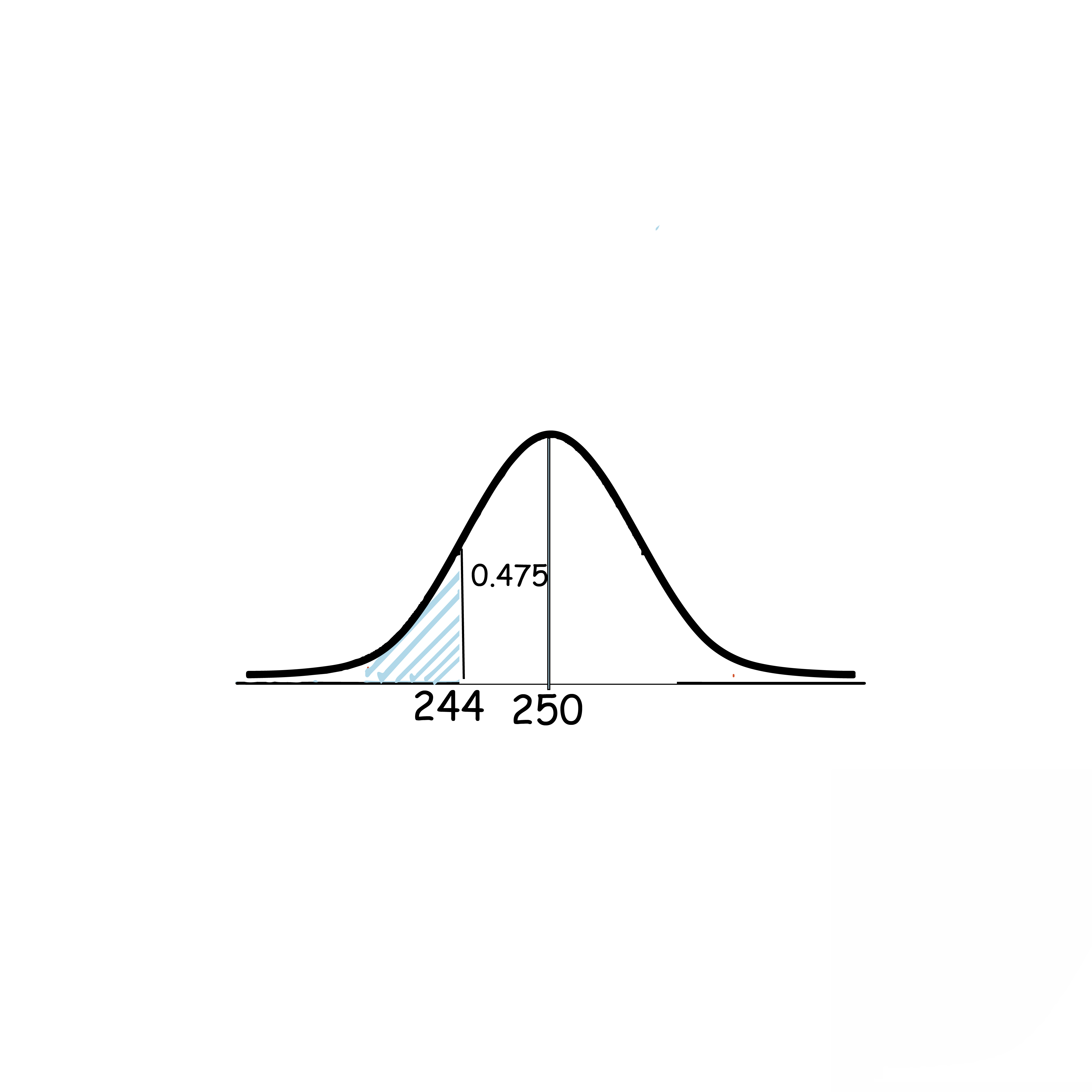
244=250-6

       =$\mu -2\sigma$

P(X<244)=0.5-0.475

                 =0.025

التوزيع الطبيعي المعياري:

التوزيع  الطبيعي المعياري: هو توزيع طبيعي وسطه الحسابي (0) وانحرافه المعياري (1)و ويرمز للمتغير العشوائي الطبيعي المعياري بالرمز:

Z~N(0,1)

و يمكن استخدام جدول التوزيع الطبيعي المعياري لإيجاد المساحة تحت المنحنى الطبيعي المعياري, (وهي نفسها الاحتمال),

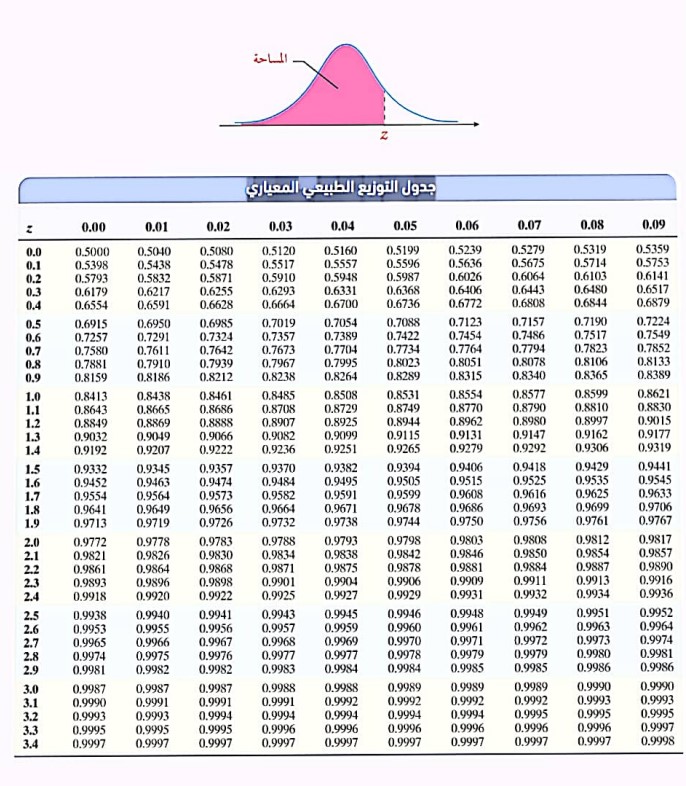
فيكون:

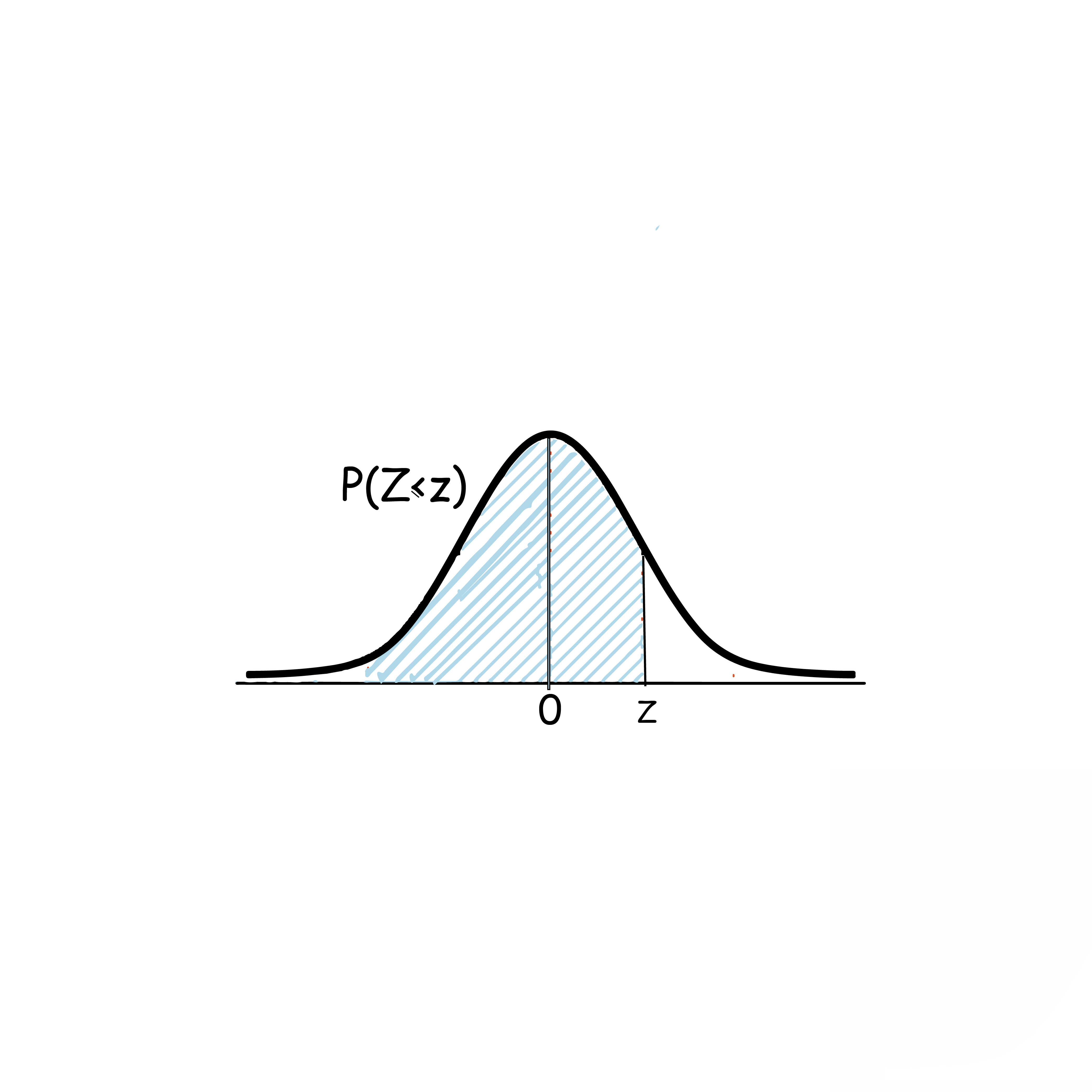
المساحة المظللة تساوي احتمال قيم المتغير العشوائي الطبيعي المعياري Z التي تقل عن (أو تساوي) القيمة المعيارية Z ,1

المساحة المظللة= $P(Z<z) \mathrm{نفسها} \mathrm{وهي} P(Z\le z)$

 ونلاحظ أن الجدول يعطي المساحة تحت المنحمى الطبيعي المعياري على يسار قيم Z الموجبة, لذلك نستخدم خصائص المنحنى الطبيعي المعياري والتماثل لقيم Z السالبة, اعتمادًا على المفاهيم التالية: (حيث Z,Z₁,Z₂ قيمة موجبة)

1)P(Z>z)1-P(Z<z)

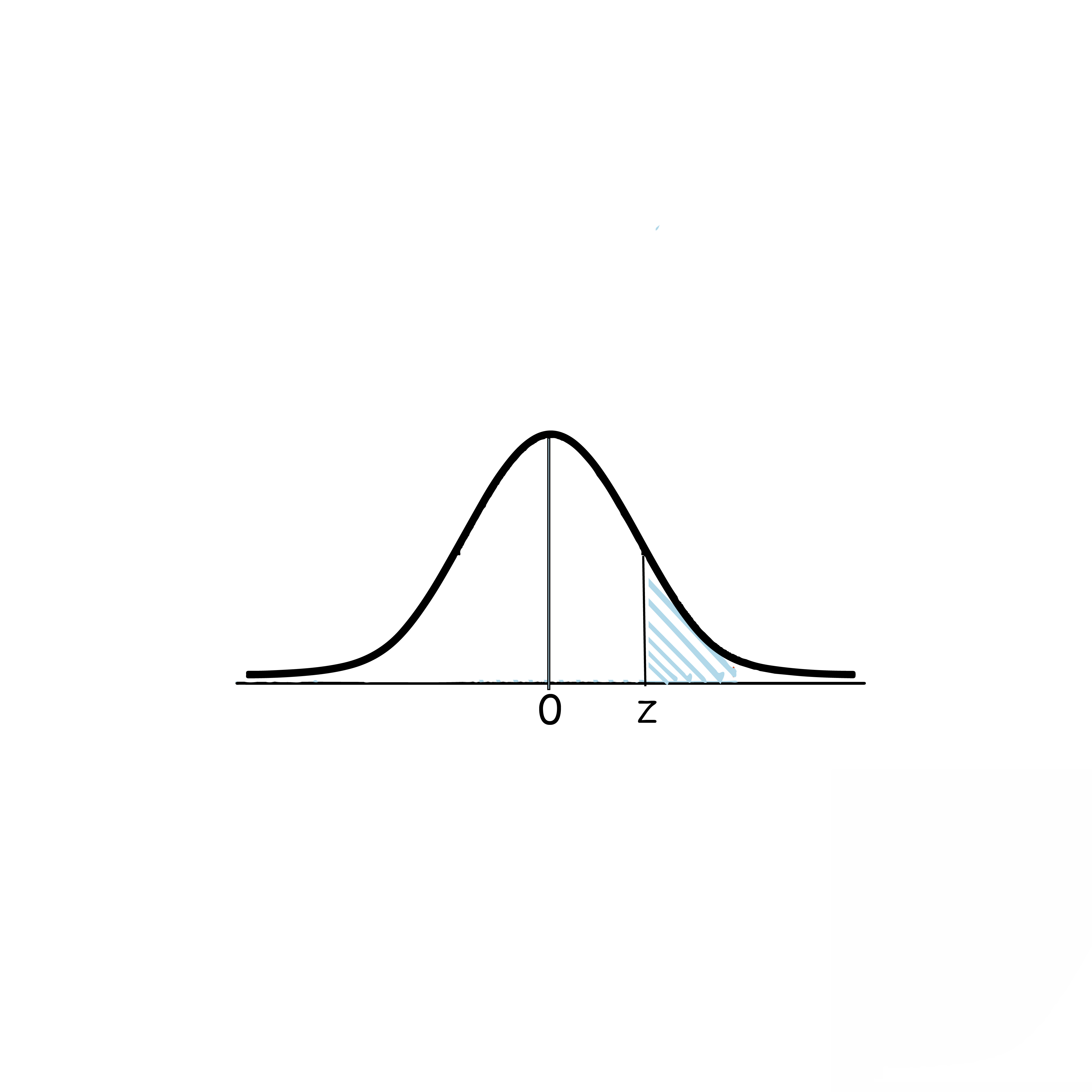
2)P(Z<-z)=P(Z>z)

                =1-P(Z<z)

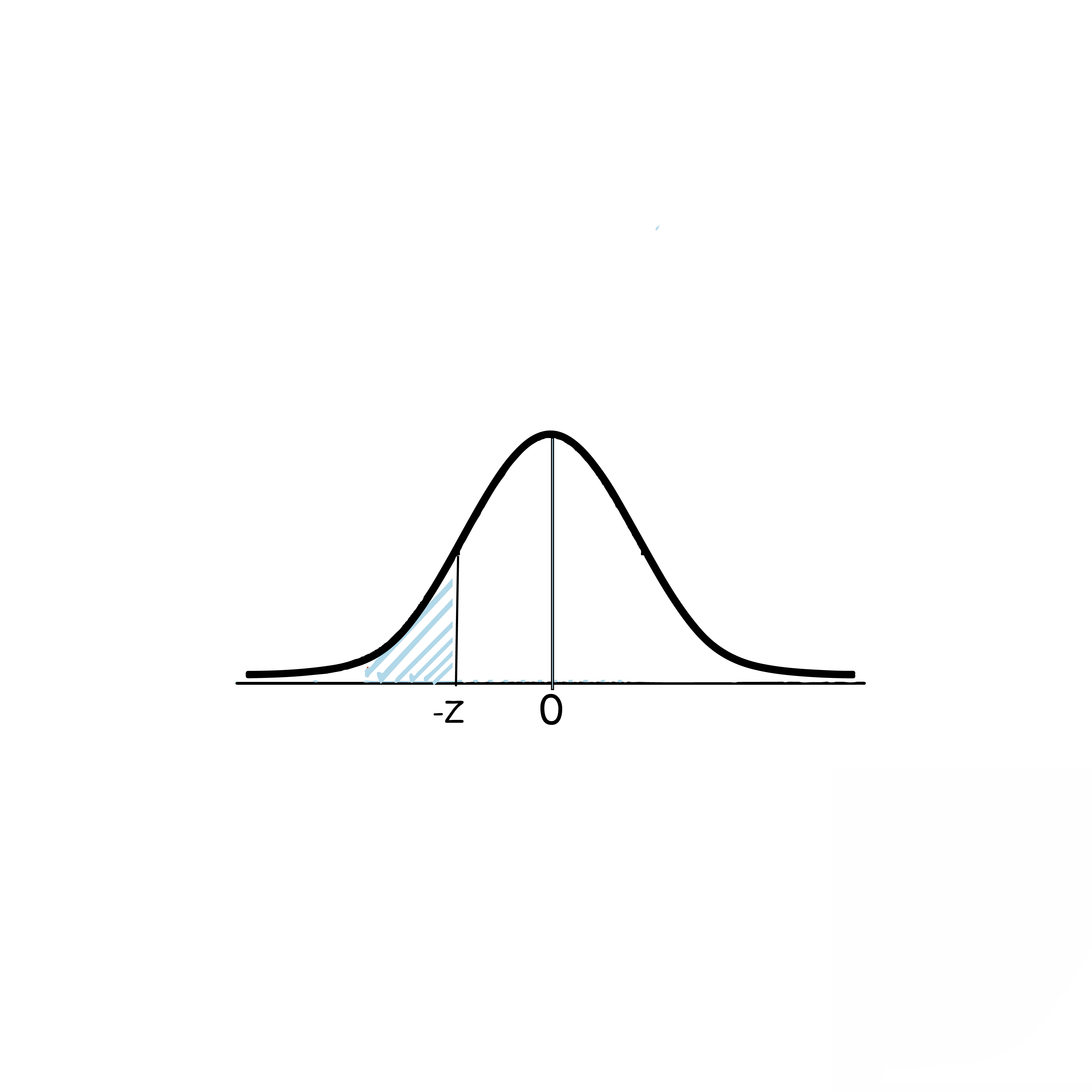
3)P(Z>-z)=P(Z<z)

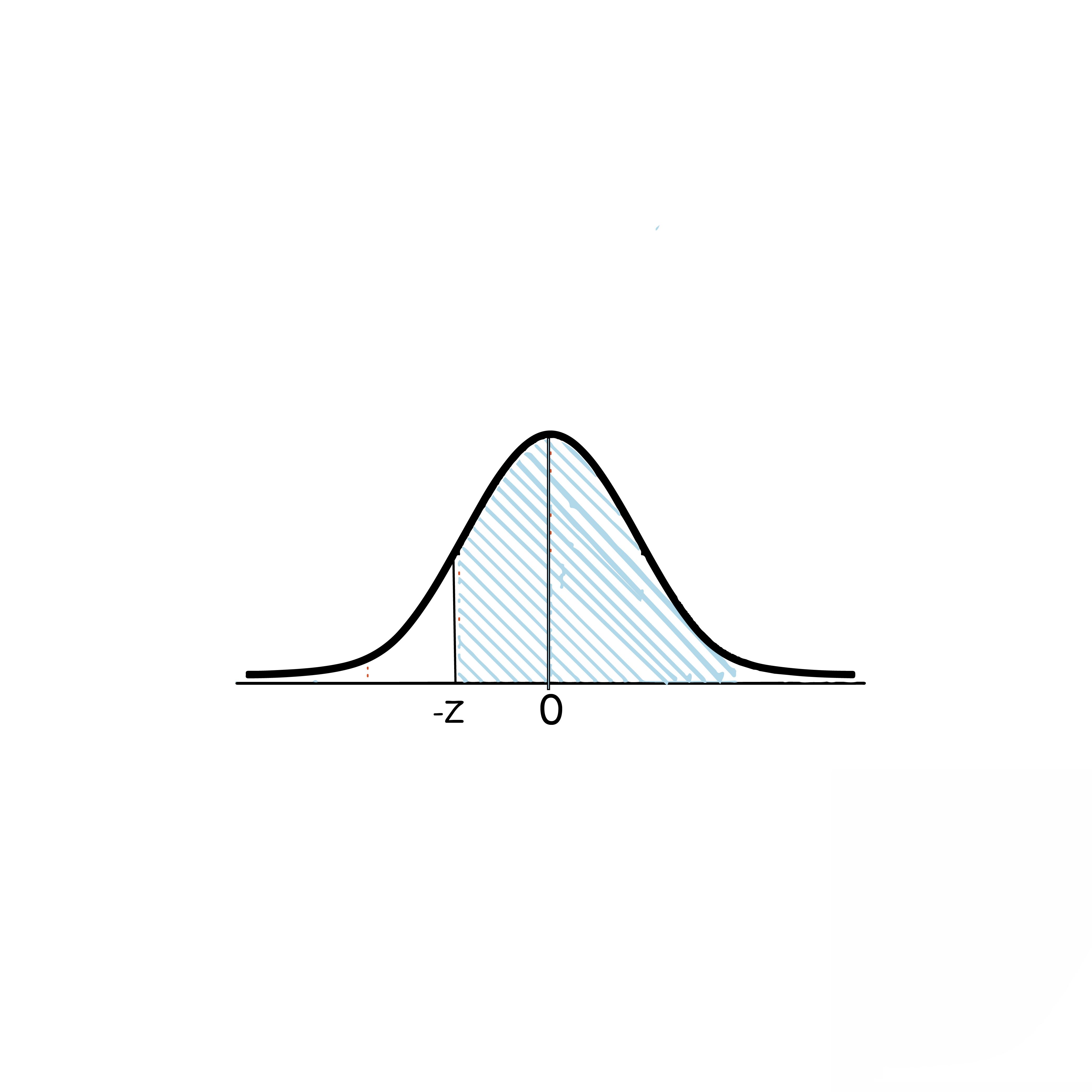
4)P(z₁<Z<z₂)=P(Z<z₂)-P(Z<z₁)

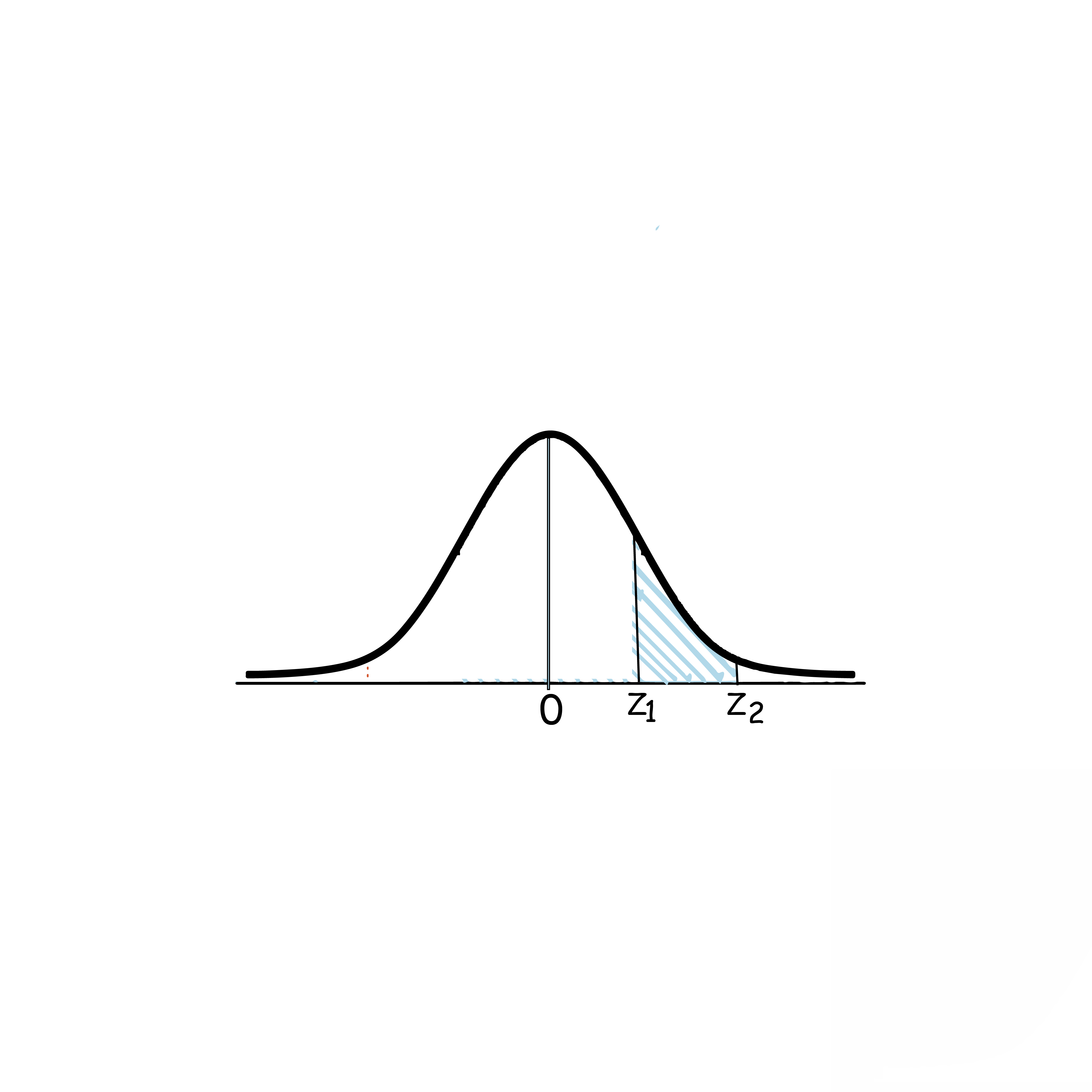
5)P(-z₂<Z<-z₁)=P(z₁<Z<z₂)

                        =P(Z<z₂)-P(Z<z₁)

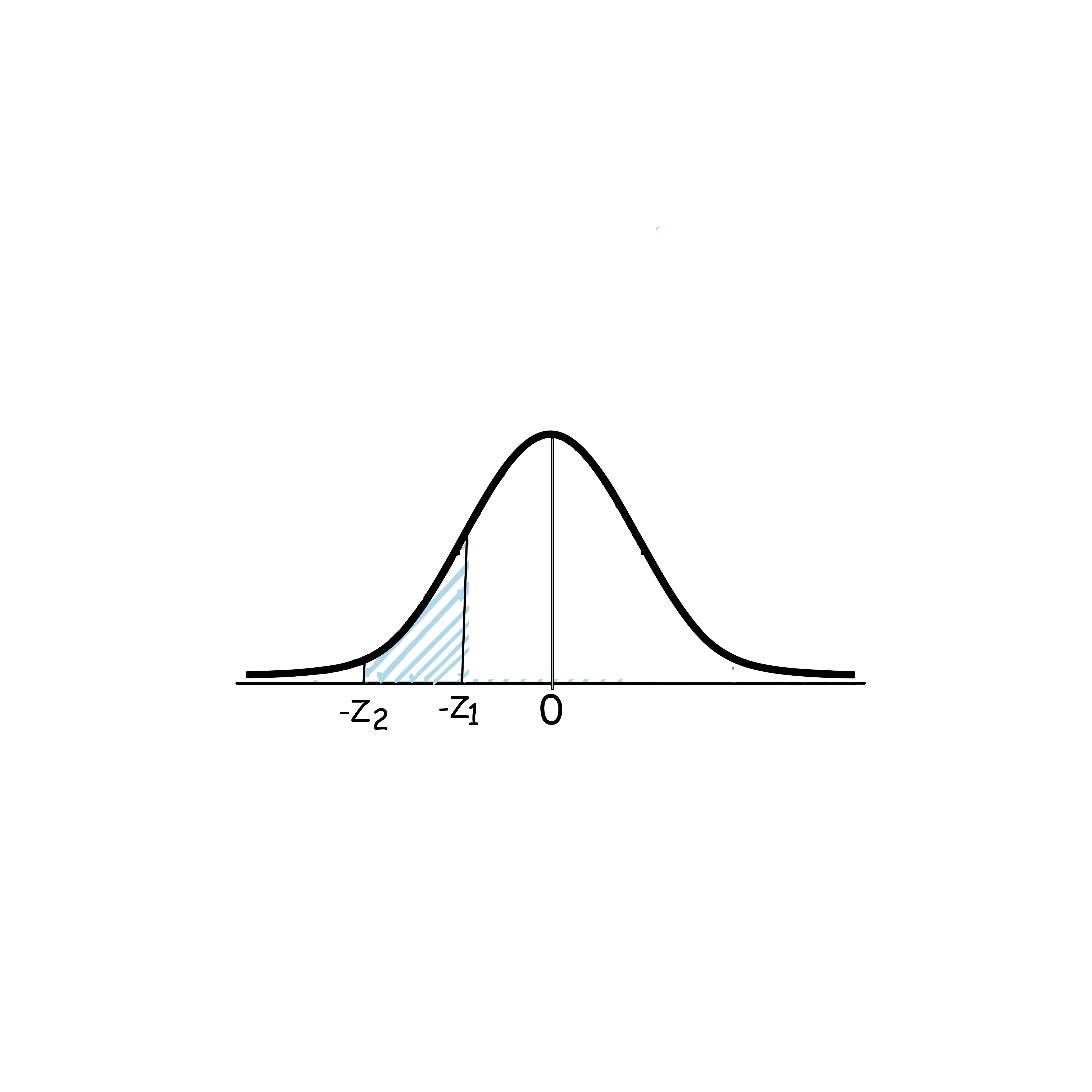
6)P(-z₁<Z<-z₂)=P(Z<z₂)-P(Z<-z₁)

                        =P(Z<z₂)+P(Z<z₁)-1

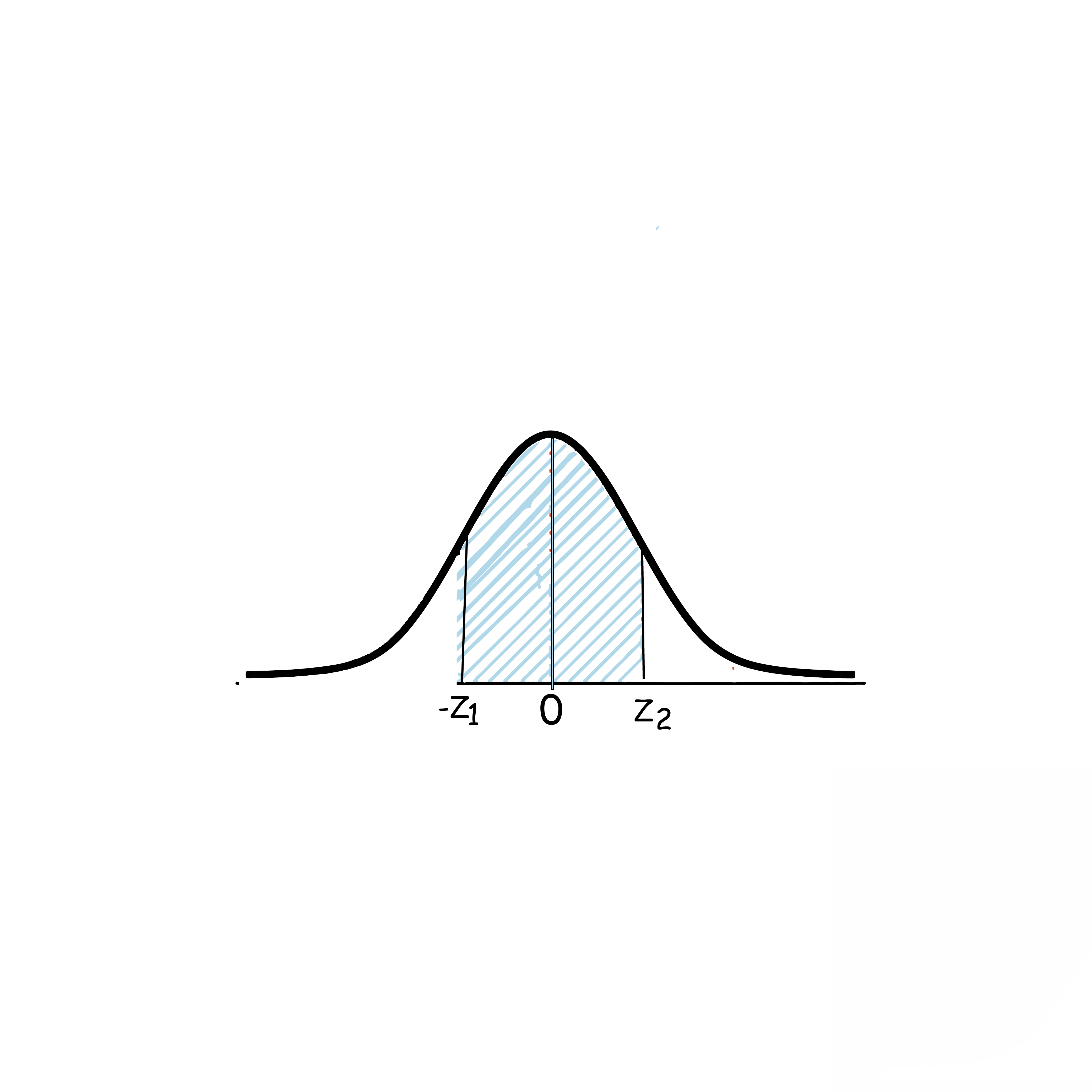
مثال3: مستخدمًا جدول التوزيع الطبيعي المعياري, جد كلًا مما يلي:

1)P(Z$\le$1.7)

الحل:

P(Z$\le$1.7)=0.9554

2)P(Z$\ge$1.7)

الحل:

P(Z$\ge$1.7)=1-P(Z>1.7)

                =1-0.9554

                =0.0446

3)P(Z>-1.08)

الحل:

P(Z>-1.08)=P(Z<1.08)

                  =0.8599

4)P(Z<-0.97)

الحل:

P(Z<-0.97)=P(Z>0.97)

                  =1-P(Z$\le$0.97)

                  =1-0.8340

                  =0.1660

5)P(-1<Z<0.5)

الحل:

P(-1<Z<0.5)=P(Z<0.5)-P(Z<-1)

                    =P(Z<0.5)+P(Z<-1)-1

                    =0.6915+0.8413-1

                    =0.5328

إيجاد احتمال المتغير العشوائي الطبيعي غير المعياري:

يمكن تحويل المتغير العشوائي الطبيعي غير المعياري $(X~N(\mu ,{\sigma }^2\left)\right)$ إلى متغير طبيعي معياري, (Z~N(0,1)) باستخدام القيم المعيارية Z المقابلة للقيم الحقيقية X حسب الصيغة:

$Z=\frac{x-\mu }{\sigma }$

بحيث نستخدم جدول التوزيع الطبيعي المعياري لإيجاد الاحتمال.

مثال 4: إذا كان X متغيرًا عشوائيًا طبيعيًا, حيث:

X~N(40,25)

فجد كلًا مما يلي:

1)P(X$\ge$42.5)

الحل: الوسط الحسابي: $\mu =40$

الانحراف المعياري: $\sigma =5$

P(X$\ge$42.5)=P(Z$\ge \frac{42.5-40}{5}$)

                   =P(Z$\ge$0.5)

                   =1-P(Z<0.5)

                   =1-0.6915

                   =0.3085

2)P(35<X<40)

الحل:

P(35<X<40)=P($\frac{35-40}{5}<Z<\frac{40-40}{5}$)

                     =P(-1<Z<0)

                     =P(Z<0)-P(Z<-1)

                     =P(Z<0)+P(Z<1)-1

                     =0.5000+0.8413-1

                     =0.3413

3)P(X$\le$33)

الحل:

P(X$\le$33)=P(Z$\le \frac{33-40}{5}$)

                =P(Z$\le$-1.4)

                =1-P(Z$\le$1.4)

                =1-0.9192

                =0.0807

مثال 5: في دراسة شملت طلبة إحدى الجامعات, كان معدل الطلبة يتبع توزيعًا طبيعيًا بوسط حسابي 73, وانحراف معياري 8 علامات.

إذا اختير طالب عشوائيًا, ما احتمال:

1)أن يكون معدله أعلى من 75:

الحل:

$$\begin{gathered} \sigma =8 , \mu =73 \\ P(X>75)=P(Z>\frac{75-73}{8}) \\ =P(Z>0.25) \\ =1-P(Z\le 0.25) \\ =1-0.5987 \\ =0.4013 \end{gathered}$$ 

2)أن يكون معدله أعلى من 69.

الحل:

$$\begin{gathered} P(X>69)=P(Z>\frac{69-73}{8}) \\ =P(Z>-0.5) \\ =P(Z<0.5) \\ =0.6915 \end{gathered}$$

3)أن يكون معدله محصورًا بين 75 و 83.

الحل:

$$\begin{gathered} P(75<X<83)=P(\frac{75-73}{8}<Z<\frac{83-73}{8}) \\ =P(0.25<Z<1.25) \\ =P(Z<1.25)-P(Z<0.25) \\ =0.8944-0.5987 \\ =0.2957 \end{gathered}$$

إيجاد قيمة المتغير العشوائي إذا علم الاحتمال:

عند معرفة الاحتمال, نجد قيم Z التي تقابل هذا الاحتمال باستخدام جدول التوزيع الطبيعي المعياري وخصائصه, ثم نجد قيمة X المقابلة لقيمة Z الناتجة.

مثال 6: إذا كان X متغيرًا عشوائيًا طبيعيًا وسطه الحسابي 25 وانحرافه المعياري 7 فجد قيمة x التي تحقق الاحتمال المعطى في كل مما يلي:

1)P(X<x)=0.994

الحل: لاحظ أن 0.5<0.994 (وأن المساحة على اليسار), مما يعني أن Z المقابلة لقيمة x هي قيمة موجبة

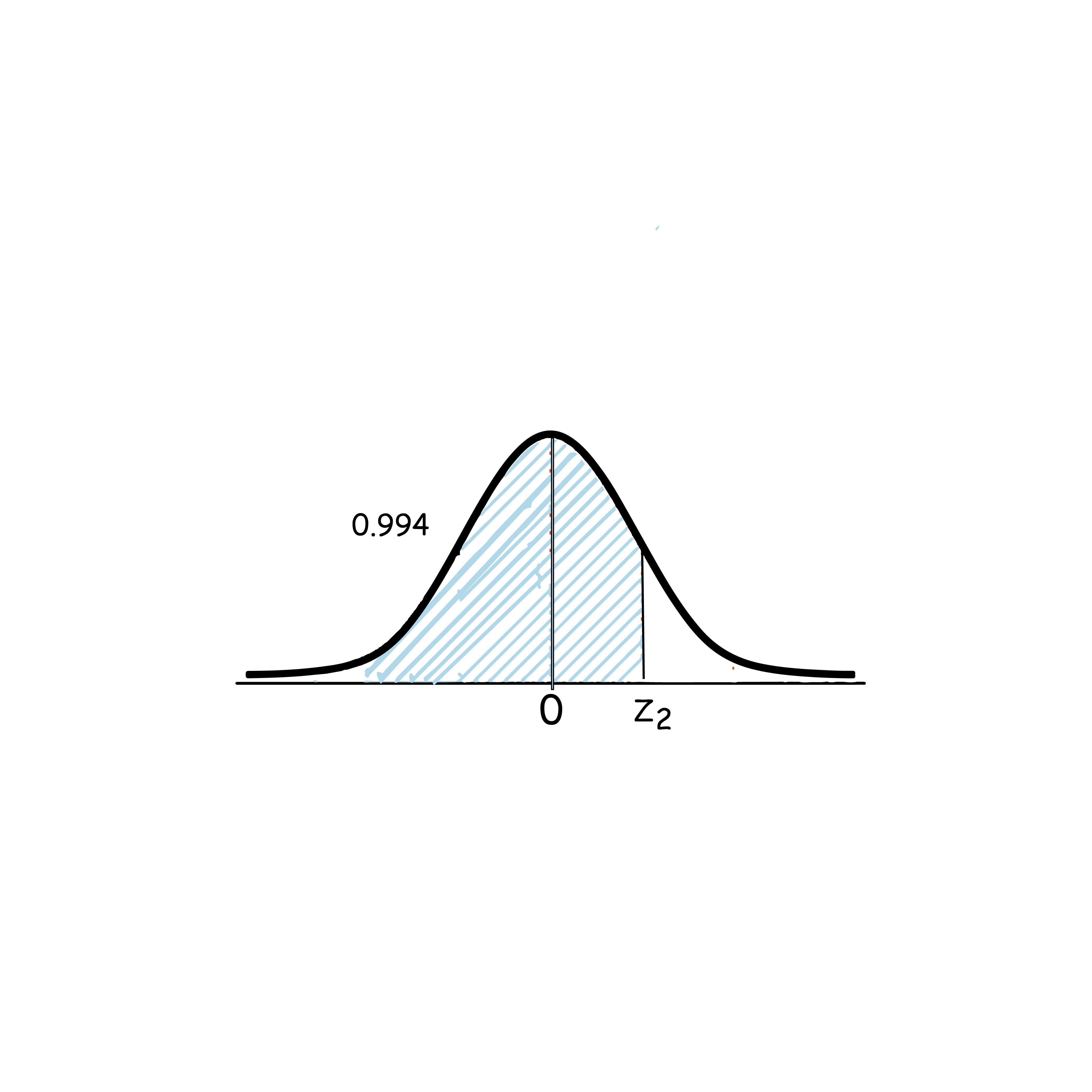
من جدول التوزيع الطبيعي المعياري, نجد أن هذه المساحة تقابل Z=2.51

$$\begin{gathered} Z=\frac{x-\mu }{\sigma } \\ 2.51=\frac{x-25}{7} \\ x=42.57 \end{gathered}$$

2)P(X<x)=0.3446

الحل: لاحظ أن: 0.5>0.3446, وأن المساحة على اليسار مما يعني أن Z سالبة 

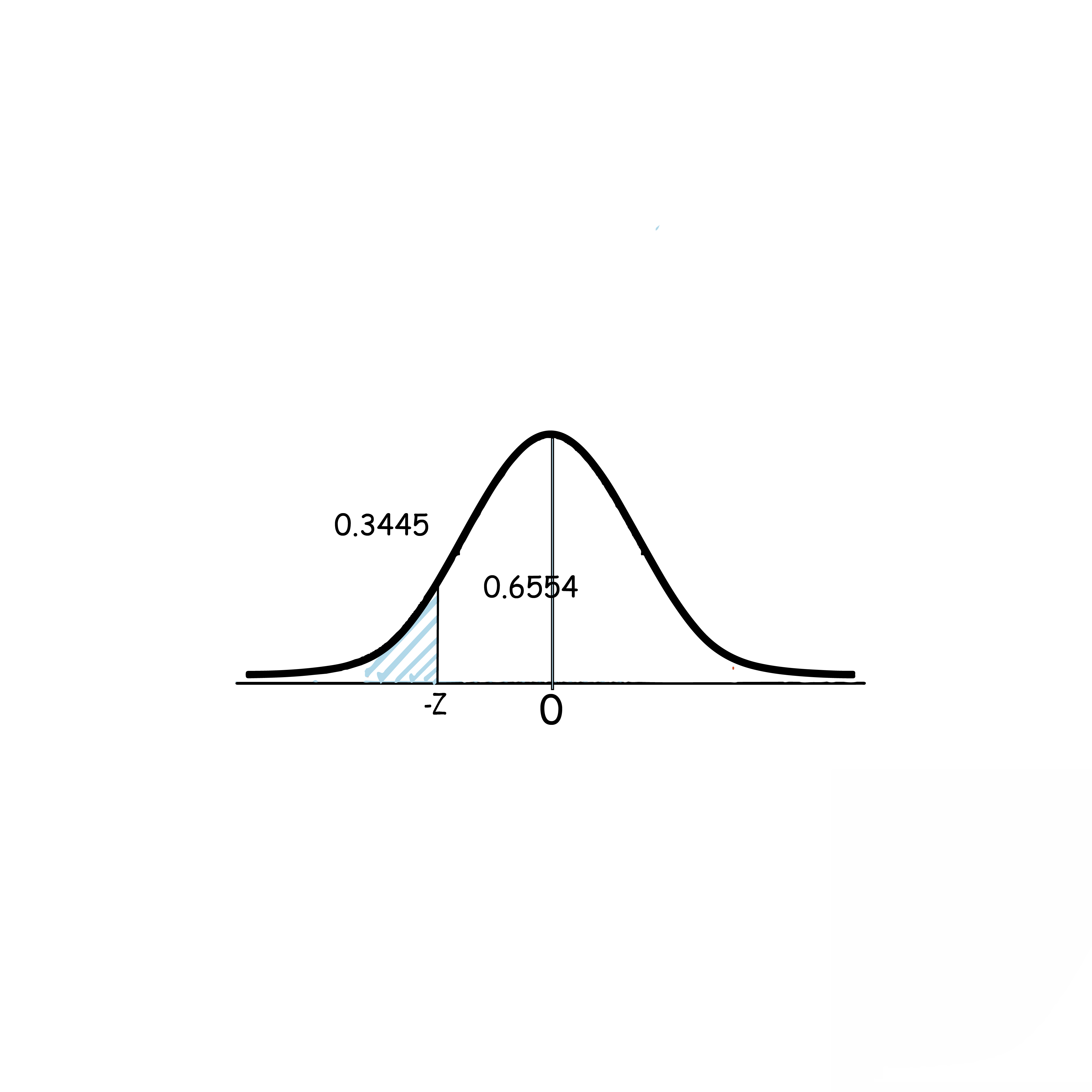
P(Z<-z)=1-P(Z<z)

0.3446=1-P(Z<z)

P(Z<z)=0.6554

من الجدول:

Z=0.4

-Z=-0.4

-Z=$\frac{x-\mu }{\sigma }$

-0.4=$\frac{x-25}{7}$

x=22.2

3)P(X>x)=0.79

الحل: لاحظ أن: 0.5<0.79 , وأن المساحة على اليمين مما يعني أن قيمة z قيمة سالبة.

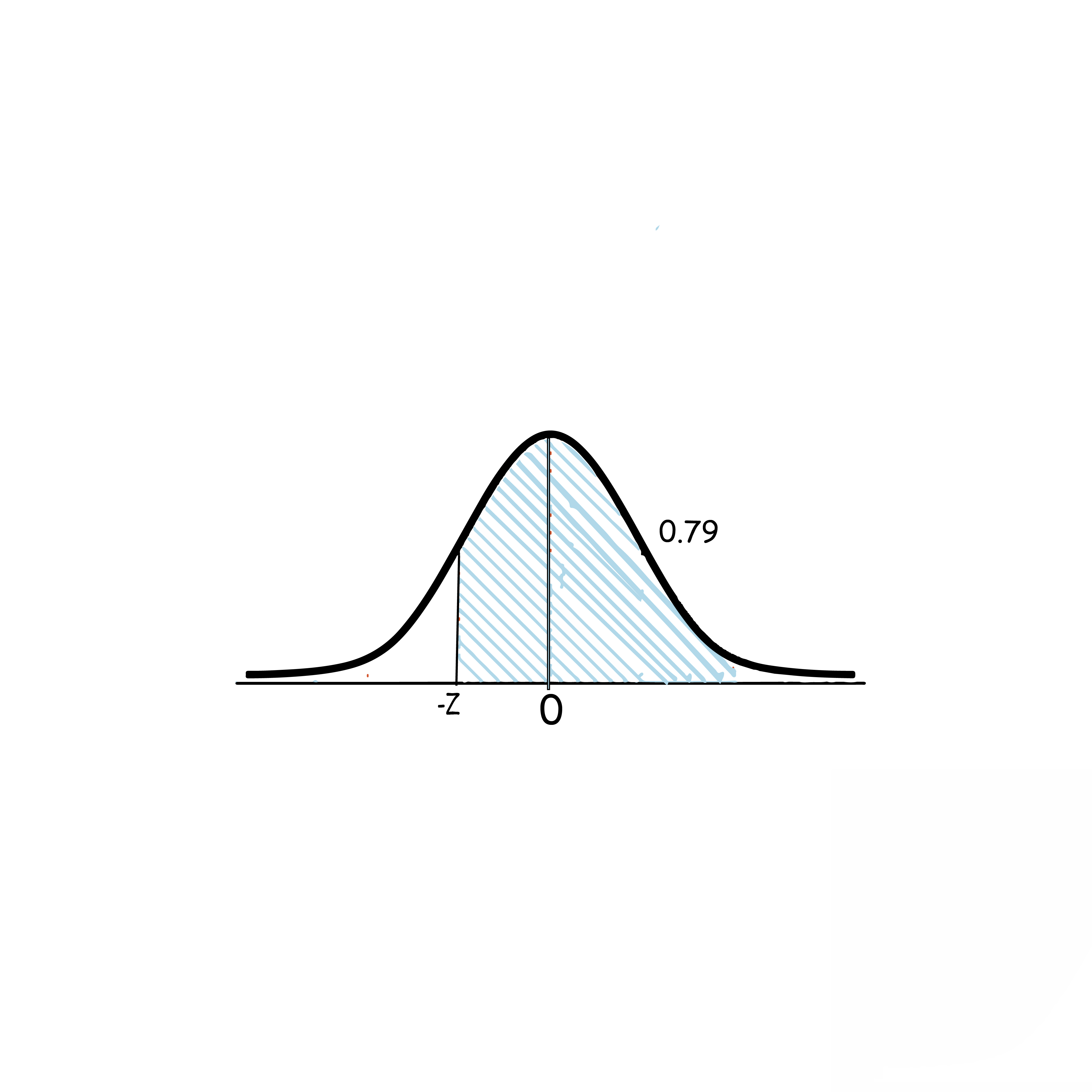
P(Z>-z)=P(Z<z)

من الجدول نجد أن أقرب قيمة إلى 0.79 هي 0.7910 تقابل

z=0.81

-z=0.81

$$\begin{gathered} -z=\frac{x-\mu }{\sigma } \\ -0.81=\frac{x-25}{7} \\ x=19.33 \end{gathered}$$

4)P(X$\ge$x)=0.063

الحل: لاحظ أن: 0.5>0.063, وأن المساحة على اليمين, مما يعني أن قيمة z موجبة

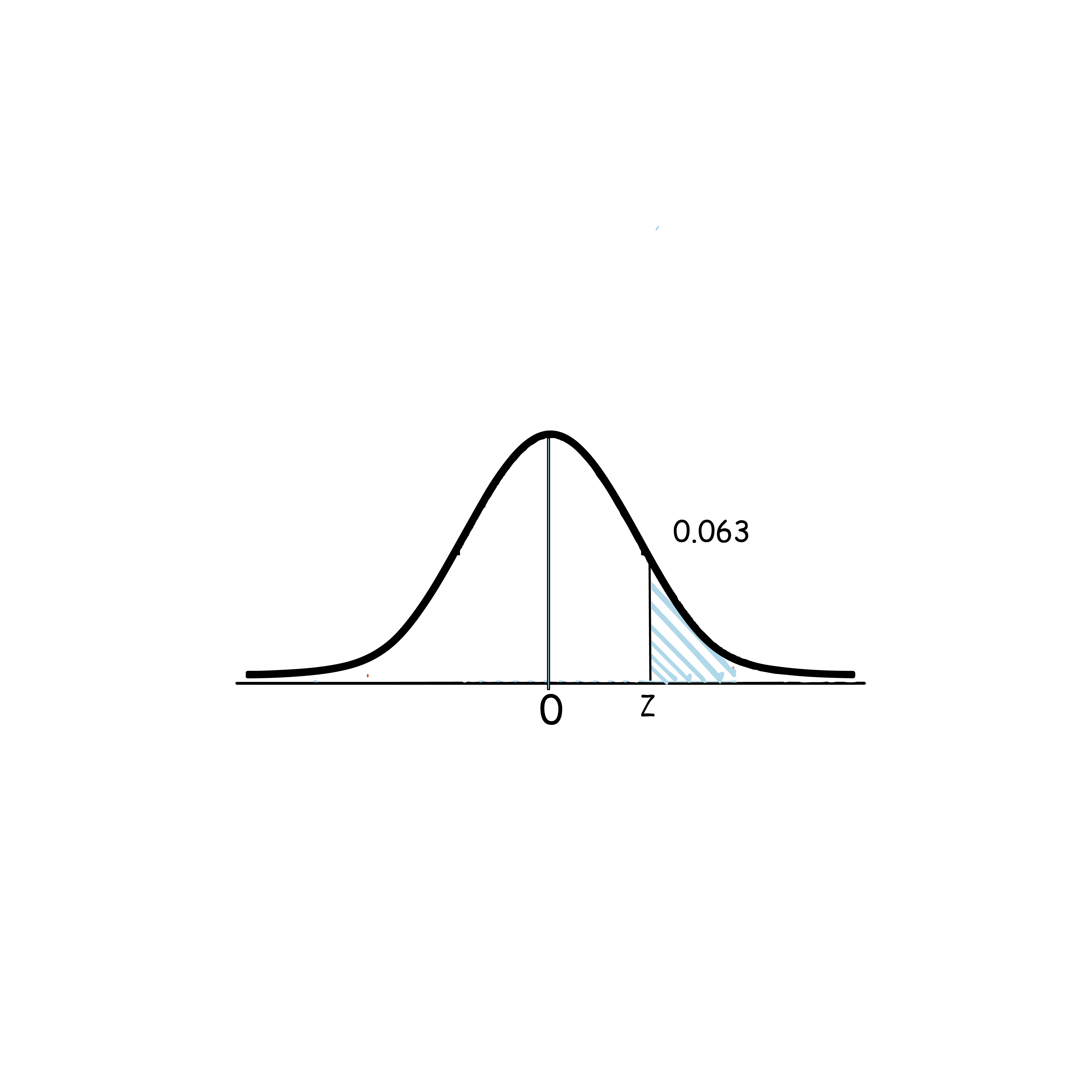
P(Z>z)=1-P(Z$\le$z)

0.063=1-P(Z$\le$z)

P(Z$\le$z)=0.9370

من الجدول: z=1.53

$$\begin{gathered} z=\frac{x-\mu }{\sigma } \\ 1.53=\frac{x-25}{7} \\ x=35.71 \end{gathered}$$

إيجاد الوسط الحسابي أو الانحراف المعياري إذا علم الاحتمال:

يمكن توظيف الخصائص السابقة في حل مسائل عملية وإيجاد الوسط الحسابي أو الانحراف المعياري لتوزيع طبيعي.

مثال7: 

يمثل $X~N(500,{\sigma }^2)$ المتغير العشوائي الطبيعي لكتلة حبة دواء (بالميلغرام) التي ينتجها أحد مصانع الأدوية إذا زادت كتلة 4% منها على mg 510 فجد الانحراف المعياري لكتل حبات الدواء.

الحل:

$4\%=0.04 , \mu =500 mg$

لاحظ أن 0.5>0.04 , وأن المساحة على اليمين مما يعني أن قيمة z موجبة

$$\begin{gathered} P(Z>z)=1-P(Z\le z) \\ 0.05=1-P(Z\le z) \\ P(Z\le z)=0.96 \end{gathered}$$

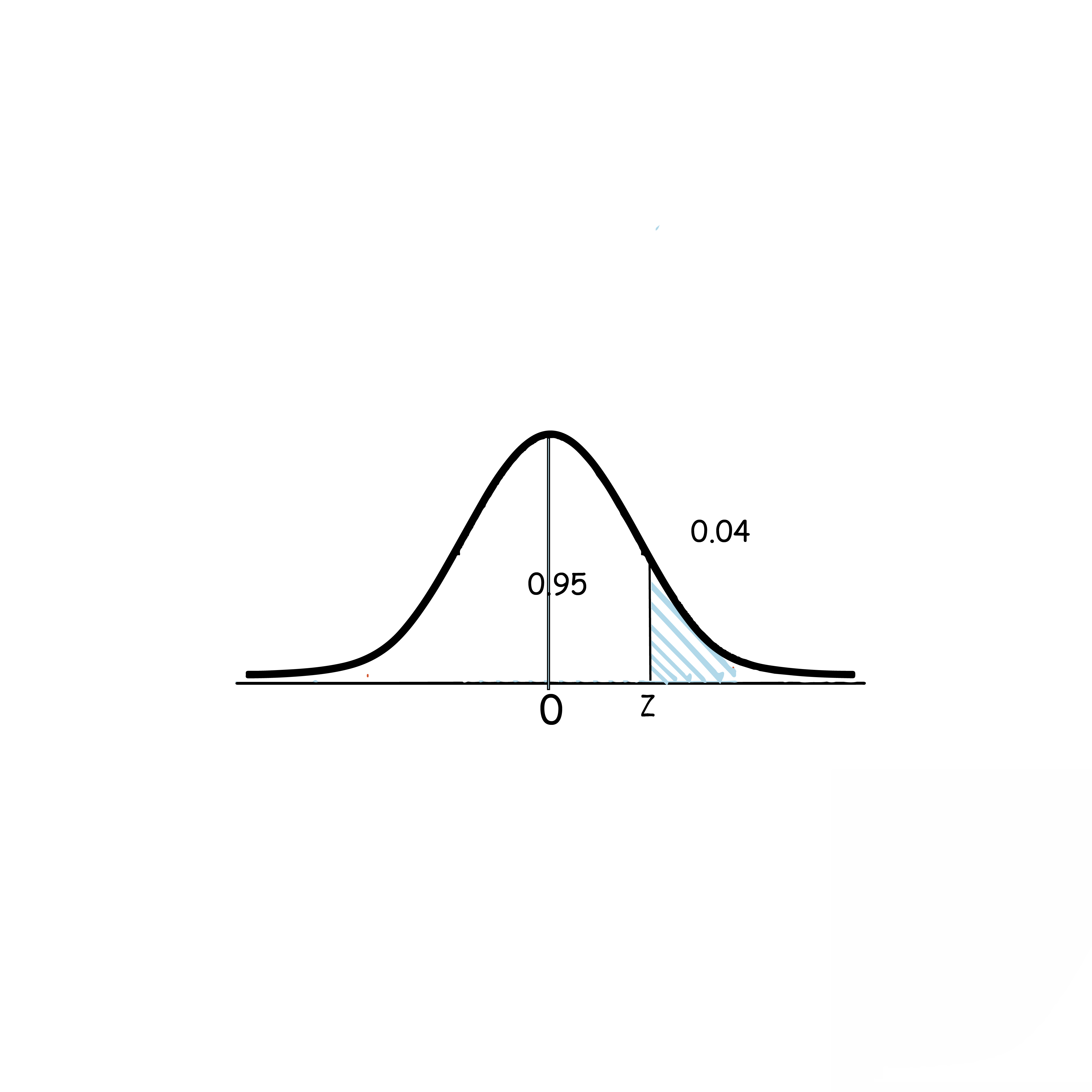
من الجدول نجد أقرب قيمة على الاحتمال 0.96, نجدها 0.9599 تقابل z=1.75

$$\begin{gathered} z=\frac{x-\mu }{\sigma } \\ 1.75=\frac{510-500}{\sigma } \\ \sigma =\frac{10}{1.75} \\ \sigma \approx 5.71 \end{gathered}$$

الانحراف المعياري يساوي تقريبًا 5.75 mg