lesson questions solve - Grade التوجيهي علمي - رياضيات فصل ثاني - JO Academy school

‎الدرس الثاني: التوزيع الطبيعي

مسألة اليوم :

إذا كان الزمن الذي تستغرقه الكهرباء في بطارية هاتف محمول قبل أن تنفد تمامًا

يتبع توزيعا طبيعيا وسطه الحسابي 36 ساعة ، وانحرافه المعياري 5 ساعات ،

فما احتمال أن تعمل البطارية مدة 27 ساعة على الأقل؟

الحل:

ليكن T الزمن الذي تستغرقه البطارية قبل نفادها

$\begin{array}{l} P a g e 178 T ~ N (36, {(5)}^{2}), P (T > 27) = ? \\ S o l u t i o n : \\ P (T = x) = P (Z > \frac{x - μ}{σ}) \\ P (T > 27) = P (Z > \frac{27 - 36}{5}) = P (Z > - 1.8) \\ = P (Z < 1.8) f r o m t h e t a b l e \\ = 0.9641 \end{array}$

أتحقّق من فهمي ص 182 .

إذا اتخذ التمثيل البياني لأطوال مجموعة من طلبة الصف السابع شكل المنحنى الطبيعي ، أجد كلا مما يأتي:

$a$ النسبة المئوية للطلبة الذين تقع أطوالهم فوق الوسط الحسابي

الحل:

النسبة المئوية للطلبة الذين تقع أطوالهم فوق الوسط الحسابي هي 50% .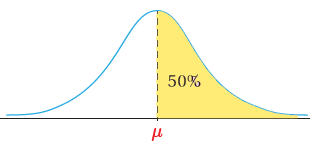

وذلك من خواص منحنى التوزيع الطبيعي (تماثل البيانات حول الوسط الحسابي)

$b$ النسبة المئوية للطلبة الذين لا يزيد البُعْد بين أطوالهم والوسط الحسابي على انحراف معياري واحد.

الحل:

النسبة المئوية للطلبة الذين لا يزيد البعد بين أطوالهم و الوسط الحسابي على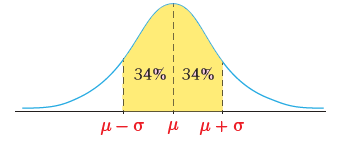

انحراف معياري واحد هي 68% وذلك بالاستناد للقاعدة التجريبية مباشرة.

$c$ النسبة المئوية للطلبة الذين تقل أطوالهم عن الوسط الحسابي بمقدار لا يزيد على انحرافين معياريين.

الحل:

النسبة المنوية للطلبة الذين تقل أطوالهم عن الوسط الحسابي بمقدار لا يزيد على انحرافين معياريين هي: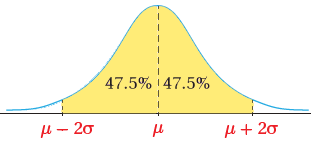

$= \frac{1}{2} (95 %) = 47.5 %$ أو هي : $34 % + 13.5 % = 47.5 %$

$d$ النسبة المئوية للطلبة الذين تقل أطوالهم عن الوسط الحسابي بمقدار لا يزيد على ثلاثة انحرافات معيارية،

أو تزيد عليه بمقدار لا يزيد على انحرافين معياريين.

الحل:

النسبة المئوية للطلبة الذين تقل أطوالهم عن الوسط الحسابي بمقدار لا يزيد على ثلاثة انحرافات معيارية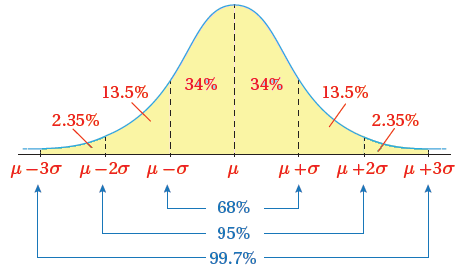

أو تزيد عليه بمقدار لا يزيد على انحرافين معياريين هي: $= \frac{1}{2} (95 %) + \frac{1}{2} (95 %) = 97.35 %$

أتحقّق من فهمي ص 184

صناعة : إذا دل المُتغيّر العشوائي X على طول قطر رأس مثقب (بالمليمتر) تنتجه آلة في مصنع، حيث: $X ~ N (30, {(0.4)}^{2})$ ، فأجد كُلا مما يأتي:

$\begin{array}{l} a P (X > 30) = ?; X ~ N (30, {(0.4)}^{2}) \\ S o l u t i o n : \\ P (X > 30) = P (X > μ) = 0.5 F r o m t h e c u r v e \end{array}$

$\begin{array}{l} b P (29.6 < X < 30.4) = ?; X ~ N (30, {(0.4)}^{2}) \\ S o l u t i o n : \\ P (29.6 < X < 30.4) = P (30 - 0.4 < X < 30 + 0.4) \\ = P (μ - σ < X < μ + σ) = 0.68 F r o m t h e c u r v e \end{array}$

$\begin{array}{l} c P (29.2 < X < 30) = ?; X ~ N (30, {(0.4)}^{2}) \\ S o l u t i o n : \\ P (29.2 < X < 30) = P (30 - 2 (0.4) < X < 30) \\ = P (μ - 2 σ < X < μ) \\ = 34 % + 13.5 % = 47.5 % F r o m t h e c u r v e \end{array}$

$\begin{array}{l} d P (29.2 < X < 30.4) = ?; X ~ N (30, {(0.4)}^{2}) \\ S o l u t i o n : \\ P (29.2 < X < 30.4) = P (30 - 2 (0.4) < X < 30 + (0.4)) \\ = P (μ - 2 σ < X < μ + σ) \\ = 34 % + 13.5 % + 34 % = 81.5 % F r o m t h e c u r v e \end{array}$

اتحقق من فهمي ص 187

أجد كُلا مما يأتي: مستعملاً جدول التوزيع الطبيعي المعياري :

$\begin{array}{l} a P (Z < 1.5) = ? \\ S o l u t i o n : \\ P (Z < 1.5) = 0.9332 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} b P (Z > 0.61) = ? \\ S o l u t i o n : \\ P (Z > 0.61) = 1 - P (Z < 0.61) \\ = 1 - 0.7291 \\ = 0.2709 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} c P (Z < - 0.43) = ? \\ S o l u t i o n : \\ P (Z < - 0.43) = P (Z > 0.43) \\ = 1 - P (Z < 0.43) \\ = 1 - 0.6664 \\ = 0.3336 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} d P (Z > - 3.32) = ? \\ S o l u t i o n : \\ P (Z > - 3.23) = P (Z < 3.23) \\ = 0.9994 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} e P (- 1.4 < Z < 2.07) = ? \\ S o l u t i o n : \\ P (- 1.4 < Z < 2.07) = \\ = P (Z < 2.07) - P (Z < - 1.4) \\ = P (Z < 2.07) - P (Z > 1.4) \\ = P (Z < 2.07) - (1 - P (Z < 1.4)) \\ = 0.9808 - (1 - 0.9192) = 0.9 F r o m t h e t a b l e \end{array}$

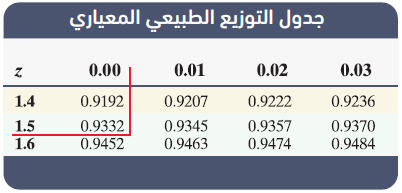
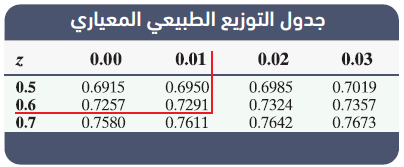
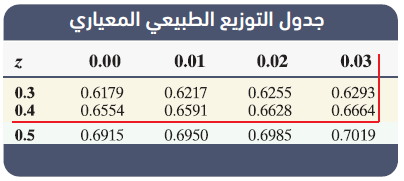
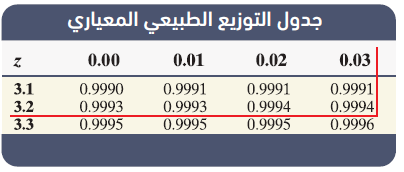
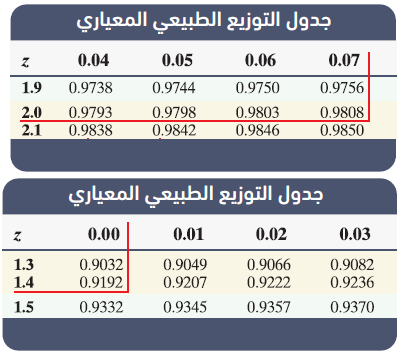
اتحقق من فهمي ص 189

إذا كان: $X ~ N (7, {(3)}^{2})$ ، فأجد كل احتمال مما يأتي. مستعملاً جدول التوزيع الطبيعي المعياري:

$\begin{array}{l} a P (X < - 2) : X ~ N (7, {(3)}^{2}) \\ S o l u t i o n : \\ P (X < - 2) = P (Z < \frac{- 2 - 7}{3}) \\ = P (Z < - 3) = P (Z > 3) \\ = 1 - P (Z < 3) = 1 - 0.9987 = 0.0013 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} b P (X > 10) : X ~ N (7, {(3)}^{2}) \\ S o l u t i o n : \\ P (X > 10) = P (Z > \frac{10 - 7}{3}) \\ = P (Z > 1) \\ = 1 - P (Z < 1) = 1 - 0.8413 = 0.1587 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} c P (4 < X \leq 13) : X ~ N (7, {(3)}^{2}) \\ S o l u t i o n : \\ P (4 < X \leq 13) = P (\frac{4 - 7}{3} < Z \leq \frac{13 - 7}{3}) \\ = P (- 1 < Z \leq 2) \\ = P (Z \leq 2) - P (Z < - 1) \\ = 0.9772 - P (Z > 1) \\ = 0.9772 - (1 - P (Z < 1)) \\ = 0.9772 - (1 - 0.8413) = 0.8185 F r o m t h e t a b l e \end{array}$

اتحقق من فهمي ص 190

أطوال: توصلت دراسة إلى أنَّ أطوال النساء في إحدى المدن تتبع توزيعًا طبيعياً ، وسطه الحسابي 165 cm . وانحرافه المعياري 3 cm .

إذا اختيرت امرأة عشوائيًا، فأجد كلا مما يأتي:

$a$ احتمال أن يكون طول المرأة أقل من 162 cm .

$\begin{array}{l} S o l u t i o n : P (X < 162) : X ~ N (165, {(3)}^{2}) \\ P (X < 162) = P (Z < \frac{162 - 165}{3}) \\ = P (Z < - 1) = P (Z > 1) \\ = 1 - P (Z < 1) \\ = 1 - 0.8413 = 0.1587 F r o m t h e t a b l e \end{array}$

$b$ احتمال أن يكون طول المرأة أكثر من 171 cm .

$\begin{array}{l} S o l u t i o n : \\ P (X > 171) : X ~ N (165, {(3)}^{2}) \\ P (X > 171) = P (Z > \frac{171 - 165}{3}) \\ = P (Z > 2) = 1 - P (Z < 2) \\ = 1 - 0.9772 = 0.0228 F r o m t h e t a b l e \end{array}$

$c$ احتمال أن يكون طول المرأة بين 162 cm و 171 cm .

$\begin{array}{l} S o l u t i o n : \\ P (162 < X < 171) : X ~ N (165, {(3)}^{2}) \\ P (162 < X < 171) = P (\frac{162 - 165}{3} < Z < \frac{171 - 165}{3}) \\ = P (- 1 < Z < 2) \\ = P (Z < 2) - P (Z < - 1) \\ = 0.9772 - P (Z > 1) \\ = 0.9772 - (1 - P (Z < 1)) \\ = 0.9772 - (1 - 0.8413) = 0.8185 F r o m t h e t a b l e \end{array}$

اتحقق من فهمي ص 194

إذا كان X مُتغْيرًا عشوائيًا طبيعيا. وسطه الحسابي 3-، وانحرافه المعياري 4 . فأجد قيمة الاحتمال المعطى في ‏كل مما يأتي:

$\begin{array}{l} a P (X < x) = 0.9877 : X ~ N (- 3, {(4)}^{2}) \\ S o l u t i o n : \\ P (X < x) = P (Z < \frac{x - - 3}{4}) = 0.9877 \\ P (Z < \frac{x + 3}{4}) = P (Z < 2.25) F r o m t h e t a b l e \\ ∴ \frac{x + 3}{4} = 2.25 \Rightarrow x + 3 = 9 ∴ x = 6 \end{array}$

$\begin{array}{l} b P (X < x) = 0.31 : X ~ N (- 3, {(4)}^{2}) \\ S o l u t i o n : S o l v i n g P (Z < - z) f i r s t l y \\ P (Z < - z) = 0.31 \\ 1 - P (Z < z) = 0.31 \Rightarrow P (Z < z) = 0.69 \\ ∴ Z = 0.5 F r o m t h e t a b l e \\ P (X < x) = P (Z < \frac{x - - 3}{4}) = 0.31 \\ P (Z < \frac{x + 3}{4}) = P (Z < - z) \\ P (Z < \frac{x + 3}{4}) = P (Z < - 0.5) \\ ∴ \frac{x + 3}{4} = - 0.5 \Rightarrow x + 3 = - 2 ∴ x = - 5 \end{array}$

$\begin{array}{l} c P (X > x) = 0.9738 : X ~ N (- 3, {(4)}^{2}) \\ S o l u t i o n : S o l v i n g P (Z > z) f i r s t l y \\ P (Z > z) = 0.9738 \\ 1 - P (Z < z) = 0.9738 \Rightarrow P (Z < z) = 0.0262 < 0.5 \\ ∴ Z = - 1.94 F r o m t h e t a b l e \\ P (X > x) = P (Z > \frac{x - - 3}{4}) = 0.9738 \\ ∴ \frac{x + 3}{4} = - 1.94 \Rightarrow x + 3 = - 7.76 ∴ x = - 10.76 \end{array}$

$\begin{array}{l} d P (X > x) = 0.2 : X ~ N (- 3, {(4)}^{2}) \\ S o l u t i o n : S o l v i n g P (Z > z) f i r s t l y \\ P (Z > z) = 0.2 d o e s n o t e x i e s t i n t a b l e b y t h e c o m p l e m e n t : \\ 1 - P (Z < z) = 0.2 \Rightarrow P (Z < z) = 0.8 > 0.5 \\ ∴ Z = 0.84 F r o m t h e t a b l e \\ P (X > x) = P (Z > \frac{x - - 3}{4}) = 0.84 \\ ∴ \frac{x + 3}{4} = 0.84 \Rightarrow x + 3 = 3.36 ∴ x = 0.36 \end{array}$

اتحقق من فهمي ص196

يُمثل $X ~ N (4.5, σ^{2})$ المُتغيّر العشوائي الطبيعي لكتل أكياس السكر (بالكيلوغرام) التي ينتجها أحد المصانع.

إذا زادت كتلة 3 % فقط منها على 4.8 kg فأجد الانحراف المعياري لكتل أكياس السكر .

$\begin{array}{l} P (X > 4.8) = 0.03 : X ~ N (4.5, σ^{2}) \\ S o l u t i o n : \\ 1 - P (Z < z) = 0.3 \Rightarrow P (Z < z) = 0.97 > 0.5 \\ ∴ Z = 1.88 F r o m t h e t a b l e \\ ∴ \frac{4.8 - 4.5}{σ} = 1.88 \Rightarrow 1.88 σ = 0.3 \\ ∴ σ = 0.16 \end{array}$

أتدرب وأحل المسائل

إذا اتخذ التمثيل البياني لكتل الطلبة في إحدى المحافظات منحى طبيعيًا ، فأجد كلا مما يأتي:

$1$ النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي.

الحل:

النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي هي 50 % .

(حسب خواص منحنى التوزيع الطبيعي).

$2$ النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحراف معياري واحد.

الحل:

النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحراف معياري واحد هي : $\frac{1}{2} 68 % = 34 %$

$3$ النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي بمقدار لا يقل عن انحرافين معياريين.

الحل:

النسبة المئوية للطلبة الذين تزيد كتلهم على الوسط الحسابي بمقدار لا يقل عن انحرافين معياريين هي : $\frac{1}{2} (1 - 95 %) = 2.5 %$

$4$ النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحرافين معياريين ،

أو تزيد عليه بمقدار لا يزيد على ثلاثة انحرافات معيارية.

الحل:

النسبة المئوية للطلبة الذين تقل كتلهم عن الوسط الحسابي بمقدار لا يزيد على انحرافين معياريين ،

أو تزيد عليه بمقدار لا يزيد على ثلاثة انحرافات معيارية هي: $\frac{1}{2} (95 % + 99.7 %) = 97.35 %$

إذا كان : $X ~ N (50, {(4)}^{2})$ ، فأجد كلا من الاحتمالات الآتية باستعمال القاعدة التجريبية

$\begin{array}{l} 5 P (X < 50) = ? : X ~ N (50, {(4)}^{2}) \\ S o l u t i o n : \\ P (X < 50) = 0.5 F r o m t h e t a b l e \end{array}$

إذا كان : $X ~ N (50, {(4)}^{2})$ ، فأجد كلا من الاحتمالات الآتية باستعمال القاعدة التجريبية:

$\begin{array}{l} 6 P (46 < X < 54) = : X ~ N (50, {(4)}^{2}) \\ S o l u t i o n : \\ P (46 < X < 54) = P (50 - 4 < X < 50 + 4) \\ = P (μ - σ < X < μ + σ) = 68 % \end{array}$

$\begin{array}{l} 7 P (42 < X < 62) = : X ~ N (50, {(4)}^{2}) \\ S o l u t i o n : \\ P (42 < X < 62) = P (50 - 2 (4) < X < 50 + 2 (4)) \\ = P (50 - 2 (4) < X < 50 + 2 (4)) \\ = P (μ - 2 σ < X < μ + 2 σ) \\ = \frac{1}{2} (0.95) + \frac{1}{2} (0.997) = 0.9735 \end{array}$

صناعة: يُمكِن نمذجة أطوال أقطار مسامير ينتجها مصنع بمنحنى التوزيع الطبيعي المبين في الشكل المجاور:

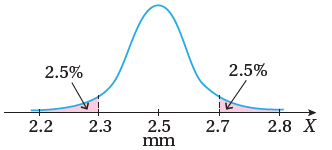
$8$ أجد الوسط الحسابي والانحراف المعياري لأطوال أقطار المسامير.

$\begin{array}{l} 8 X ~ N (2.5, {(σ)}^{2}) \\ S o l u t i o n : \\ μ = 2.5 m m \\ μ + 2 σ = 2.7 \Rightarrow 2.5 + 2 σ = 2.7 \\ ∴ σ = 0.1 m m \end{array}$

$9$ أجد النسبة المئوية للمسامير التي يزيد طول قُطر كل منها على الوسط الحسابي بما لا يزيد على انحرافين معياريين.

الحل:

النسبة المئوية للمسامير التي يزيد طول قُطر كل منها على الوسط الحسابي بما لا يزيد على انحرافين معياريين هي : $\frac{1}{2} (0.95) = 47.5 %$

$10$ أفاع: يدل المتغير العشوائي $X ~ N (100, σ^{2})$ على أطوال الأفاعي (بالستتيمتر) في أحد مجتمعاتها.

إذا كانت أطوال 68 % منها تتراوح بين 93 cm و 107 cm ، فأجد قيمة $σ^{2}$

الحل:

بما أن 68 % تقع بين $μ + σ, μ - σ$ ، فإن الوسط الحسابي :

$\begin{array}{l} 107 = μ + σ, 93 = μ - σ \\ ∴ μ = \frac{107 + 93}{2} = 100 \\ ∴ 107 = 100 + σ \\ ∴ σ = 7 \Rightarrow σ^{2} = 49 \end{array}$

أجد كلا مما يأتي مستعملا جدول التوزيع الطبيعي المعياري:

$\begin{array}{l} 11 P (Z < 0.43) = ? \\ S o l u t i o n : \\ P (Z < 0.43) = 0.6664 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 12 P (Z > 1.08) = ? \\ S o l u t i o n : \\ P (Z > 1.08) = 1 - P (Z < 1.08) \\ = 1 - 0.8599 = 0.1401 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 13 P (Z < - 2.03) = ? \\ S o l u t i o n : \\ P (Z < - 2.03) = P (Z > 2.03) \\ = 1 - P (Z < 2.03) \\ = 1 - 0.9788 = 0.0212 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 14 P (Z > 2.2) = ? \\ S o l u t i o n : \\ P (Z > 2.2) = 1 - P (Z < 2.2) \\ = 1 - 0.9861 = 0.0139 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 15 P (- 0.72 < Z < 0.72) = ? \\ S o l u t i o n : \\ P (- 0.72 < Z < 0.72) = P (Z < 0.72) - P (Z < - 0.72) \\ = P (Z < 0.72) - P (Z > 0.72) \\ = P (Z < 0.72) - (1 - P (Z < 0.72)) \\ = 2 P (Z < 0.72) - 1 \\ = 2 P (0.7642) - 1 = 0.584 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 16 P (1.5 < Z < 2.5) = ? \\ S o l u t i o n : \\ P (1.5 < Z < 2.5) = P (Z < 2.5) - P (Z < 1.5) \\ = 0.9938 - 0.9332 F r o m t h e t a b l e \end{array}$

أجد مساحة المنطقة المُظلَّلة أسفل منحنى التوزيع الطبيعي المعياري في كل مما يأتي:

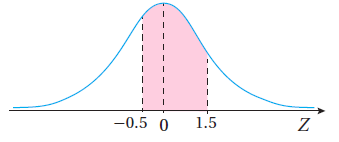
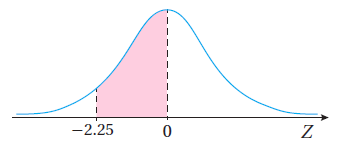
$\begin{array}{l} 17 P (- 0.5 < Z < 1.5) = ? \\ S o l u t i o n : \\ P (- 0.5 < Z < 1.5) = P (Z < 1.5) - P (Z < - 0.5) \\ = P (Z < 1.5) - P (Z > 0.5) \\ = P (Z < 1.5) - (1 - P (Z < 0.5)) \\ = P (Z < 1.5) - P (Z < 0.5) - (1) \\ = 0.9332 - 0.6915 - 1 = 0.6247 \\ F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 18 P (- 2.25 < Z < 0) = ? \\ S o l u t i o n : \\ P (- 2.25 < Z < 0) = P (Z < 0) - P (Z < - 2.25) \\ = P (Z < 0) - P (Z > 2.25) \\ = P (Z < 0) - (1 - P (Z < 2.25)) \\ = P (Z < 0) + P (Z < 2.25) - 1 \\ = 0.5 + 0.9878 - 1 = 0.4878 \\ F r o m t h e t a b l e \end{array}$

أجد القيمة المعيارية Z التي تحقق كل احتمال مما يأتي:

$\begin{array}{l} 19 P (Z < z) = 0.7642 \\ S o l u t i o n : \\ z = 0.72 D i r e c t l y F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 20 P (Z > z) = 0.3720 \\ S o l u t i o n : \\ B e c a u s e 0.3720 < 0.5 \\ ∴ P (Z < z) = 1 - 0.3720 = 0.6280 \\ ∴ z = 0.33 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 21 P (Z > z) = 0.8531 \\ S o l u t i o n : \\ B e c a u s e 0.8531 > 0.5 ∴ z < 0 \\ ∴ z = - 10.5 F r o m t h e t a b l e \end{array}$

إذا كان: $X ~ N (- 3, 25)$ ، فأجد كل احتمال مما يأتي : مستعملا جدول التوزيع الطبيعي المعياري:

$\begin{array}{l} 22 P (X < 2) = : X ~ N (- 3, 25) \\ S o l u t i o n : \\ P (X < 2) = P (Z < \frac{2 - - 3}{5}) \\ = P (Z < 1) = 0.8413 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 23 P (X > 4.5) = : X ~ N (- 3, 25) \\ S o l u t i o n : \\ P (X > 4.5) = P (Z > \frac{4.5 - - 3}{5}) \\ = P (Z > 1.5) = 1 - P (Z < 1.5) \\ = 1 - 0.9332 = 0.0668 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 24 P (- 5 < X < - 3) = : X ~ N (- 3, 25) \\ S o l u t i o n : \\ P (- 5 < X < - 3) = P (\frac{- 5 - - 3}{5} < Z < \frac{- 3 - - 3}{5}) \\ = P (- 0.4 < Z < 0) \\ = P (Z < 0) - P (Z < - 0.4) \\ = P (Z < 0) - P (Z > 0.4) \\ = P (Z < 0) - (1 - P (Z < 0.4)) \\ = P (Z < 0) + P (Z < 0.4) - (1) \\ = 0.5 + 0.6554 - (1) = 0.1554 F r o m t h e t a b l e \end{array}$

إذا كان X متغيرا عشوائيًا طبيعياً. وسطه الحسابي 30 وانحرافه المعياري 10 فأجد قيمة x التي تحقق الاحتمال المعطى في كل مما يأتي:

$\begin{array}{l} 25 P (X < x) = 0.99 : X ~ N (30, {(10)}^{2}) \\ S o l u t i o n : \\ P (X < x) = 0.99 \Rightarrow z = 2.33 F r o m t h e t a b l e \\ ∴ \frac{x - 30}{10} = 2.33 \Rightarrow x - 30 = 23.3 \\ \Rightarrow x = 53.3 \end{array}$

$\begin{array}{l} 26 P (X > x) = 0.1949 : X ~ N (30, {(10)}^{2}) \\ S o l u t i o n : \\ P (Z < z) = 1 - 0.1949 = 0.8051 \\ z = 0.86 F r o m t h e t a b l e \\ \frac{x - 30}{10} = 0.86 \Rightarrow x - 30 = 8.6 \\ \Rightarrow x = 38.6 \end{array}$

$\begin{array}{l} 27 P (X < x) = 0.35 : X ~ N (30, {(10)}^{2}) \\ S o l u t i o n : \\ B e c a u s e P (X < x) = 0.35 < 0.5 ∴ z < 0 \\ P (Z < - z) = P (Z > z) \\ = 1 - P (Z < z) = 0.35 \\ ∴ P (Z < z) = 0.65 \Rightarrow z = - 0.39 F r o m t h e t a b l e \\ \frac{x - 30}{10} = - 0.39 \Rightarrow x - 30 = - 3.9 \\ \Rightarrow x = 26.1 \end{array}$

$\begin{array}{l} 28 P (X > x) = 0.05 : X ~ N (30, {(10)}^{2}) \\ S o l u t i o n : \\ P (Z > z) = 1 - 0.05 = 0.95 \Rightarrow z = 1.64 F r o m t h e t a b l e \\ \frac{x - 30}{10} = 1.64 \Rightarrow x - 30 = 16.4 \\ \Rightarrow x = 46.4 \end{array}$

رياضة: تتبع أطوال لاعبي كرة السلة توزيعًا طبيعياً. وسطه الحسابي 185 cm ، وانحرافه المعياري 5 cm .

إذا اختير لاعب عشوائيًا ، فأجد كلا ممما يأتي:

$29$ احتمال أن يزيد طول اللاعب على 175 cm .

$\begin{array}{l} 29 P (X > 175) = : X ~ N (185, {(5)}^{2}) \\ S o l u t i o n : \\ P (X > 175) = P (Z > \frac{175 - 185}{5}) \\ = P (Z > - 2) \\ = P (Z < 2) = 0.9772 F r o m t h e t a b l e \end{array}$

$30$ احتمال أن يتراوح طول اللاعب بين 180 cm و 190 cm .

$\begin{array}{l} 30 P (180 < X < 190) = : X ~ N (185, {(5)}^{2}) \\ S o l u t i o n : \\ P (180 < X < 190) = P (\frac{180 - 185}{5} < Z < \frac{190 - 185}{5}) \\ = P (- 1 < Z < 1) \\ = P (Z < 1) - P (Z < - 1) \\ = P (Z < 1) - P (Z > 1) \\ = P (Z < 1) - (1 - P (Z < 1)) \\ = 2 P (Z < 1) - (1) \\ = 2 (0.8413) - 1 = 0.6826 F r o m t h e t a b l e \end{array}$

$31$ العدد التقريبي للاعبين الذين تزيد أطوالهم على 195 cm من بين 2000 لاعب.

$\begin{array}{l} 31 P (X > 195) = : X ~ N (185, {(5)}^{2}) \\ S o l u t i o n : \\ P (X > 195) = P (Z > \frac{195 - 185}{5}) \\ = P (Z > 2) \\ = 1 - P (Z < 2) = 1 - 0.9772 = 0.0228 F r o m t h e t a b l e \\ N u m b e r o f p l a i e r s = 2000 \times 0.0228 = 46 \end{array}$

$32$ في دراسة عن أشجار الكينا في إحدى الغابات. تبين أن الوسط الحسابي لأطوال هذه الأشجار هو 6 m ،

وأن الانحراف المعياري هو 2 cm . إذا كانت أطوال الأشجار تتبع توزيعًا طبيعيًا ، فأجد احتمال أن يكون طول شجرة اختيرت عشوايًا أكثر من 9 أمتار.

$\begin{array}{l} 32 P (X > 9) = : X ~ N (6, {(2)}^{2}) \\ S o l u t i o n : \\ P (X > 9) = P (Z > \frac{9 - 6}{2}) \\ = P (Z > 1.5) \\ = 1 - P (Z < 1.5) = 1 - 0.9332 = 0.0668 F r o m t h e t a b l e \end{array}$

تعبئة: يُعبئ مصنع حبوب القهوة في أوعية من الكرتون. إذا كانت كتل الأوعية تتبع توزيعًا طبيعيًا،

وسطه الحسابي 232 g . وانحرافه المعياري 5 g . وكان المُتغيّر العشوائي يدل على كتلة الوعاء المختار عشوائي ، فأجد كلا مما يأتي:

$\begin{array}{l} 33 P (X < 224) = : X ~ N (232, {(5)}^{2}) \\ S o l u t i o n : \\ P (X < 224) = P (Z < \frac{224 - 232}{5}) \\ = P (Z < - 1.6) = P (Z > 1.6) \\ = 1 - P (Z < 1.6) = 1 - 0.945 = 0.0548 F r o m t h e t a b l e \end{array}$

$\begin{array}{l} 34 P (232 < X < x) = 0.2 : X ~ N (232, {(5)}^{2}) \\ S o l u t i o n : \\ P (232 < X < x) = P (\frac{232 - 232}{5} < Z < z) = 0.2 \\ = P (0 < Z < z) = 0.2 \\ = P (Z < z) - P (Z < 0) = 0.2 \\ = P (Z < z) - 0.5 = 0.2 \\ ∴ P (Z < z) = 0.7 ∴ z = 0.52 F r o m t h e t a b l e \\ S o; \frac{x - 232}{5} = 0.52 \Rightarrow x - 232 = 2.6 \\ \Rightarrow x = 234.6 g \end{array}$

$35$ صناعة: يُمثّل $X ~ N (μ, 169)$ ‏ المتغير العشوائي الطبيعي لطول قطر كل من إطارات دراجات هوائية (بالمليمتر) ينتجها أحد المصانع.

إذا زاد طول قطر 11 % منها على 47 cm ، فأجد الوسط الحسابى لأطوال أقطار الاطارات التي ينتجها المصنع.

$\begin{array}{l} 35 P (X > 47) = 0.11 : X ~ N (μ, 169) \\ S o l u t i o n : \\ P (X > 47) = P (Z > \frac{47 - μ}{13}) = 0.11 \\ n o w t o f i n d P (Z < z) = 0.11 \\ P (Z < z) = 1 - P (Z > z) \\ = 1 - 0.11 = 0.89 ∴ z = 1.23 F r o m t h e t a b l e \\ S o; \frac{47 - μ}{13} = 1.23 \Rightarrow μ = 31.01 \end{array}$

$36$ اختبارات: تتبع العلامات في أحد الاختبارات توزيعا طبيعيًّا، وسعه الحسابي 43. إذا كان هو المُتغيَرَ العشوائي للعلامات فأجد قيمة الانحراف المعياري،

علمًا بأن احتمال ظهور علامة أعلى من 48 هو 0.2 .

$\begin{array}{l} 36 P (X > 48) = 0.2 : X ~ N (43, {(σ)}^{2}) \\ S o l u t i o n : \\ P (X > 48) = P (Z > \frac{48 - 43}{σ}) = 0.2 \\ = P (Z > \frac{5}{σ}) = 0.2 \\ n o w t o f i n d P (Z > z) = 0.2 \\ P (Z < z) = 1 - P (Z > z) \\ = 1 - 0.2 = 0.8 ∴ z = 0.84 F r o m t h e t a b l e \\ S o; \frac{5}{σ} = 0.84 \Rightarrow σ = 5.95 \end{array}$

$37$ إذا كان: $X ~ N (μ, {(μ)}^{2})$ وكانت قيمة Z المعيارية المقابلة لقيمة x = 1 هي Z = 2 : فأجد قيمة $μ$ .

$\begin{array}{l} 37 μ = ? : X ~ N (μ, {(μ)}^{2}) \\ S o l u t i o n : \\ z = \frac{x - μ}{σ} ∴ 2 = \frac{1 - μ}{μ} \Rightarrow μ = \frac{1}{3} \end{array}$

$38$ إذا كان: $X ~ N (μ, {(σ)}^{2})$ يمثل توزيعا طبيعيًا، وكانت قيمة Z المعيارية المقابلة لقيمة x = 10

هي Z = 1 ، وكانت قيمة Z المقابلة لقيمة x = 4 هي 2-. فأجد قيمة كل من $μ$ و $σ$ .

$\begin{array}{l} 38 μ = ?, σ = ? : X ~ N (μ, {(σ)}^{2}) \\ S o l u t i o n : \\ z = \frac{x - μ}{σ} ∴ 1 = \frac{10 - μ}{σ} \Rightarrow σ = 10 - μ . .. 1 * \\ ∴ - 2 = \frac{4 - μ}{σ} \Rightarrow - 2 σ = 4 - μ . .. 2 * \\ 3 σ = 6 ∴ σ = 2 a n d μ = 8 \end{array}$

$39$ في دراسة لإدارة السير تبين أنَّ سرعة السيارات على أحد الطرق تتبع توزيعًا طبيعيًا. وسطه الحسابي 90 km/h وانحرافه المعياري 5 km/h .

إذا كانت السرعة القصوى المحددة على هذا الطريق هي 100 km/h ، وكان العدد الكلي للسيارات التي تسير على هذا الطريق في أحد الأيام

هو 1000 سيّارة ، فأجد العدد التقريبي للسيارات التي ستتجاوز السرعة المُحدّدة على الطريق في هذا اليوم.

$\begin{array}{l} 39 P (x > 100) : X ~ N (90, {(5)}^{2}) \\ S o l u t i o n : \\ P (x > 100) = P (Z > \frac{100 - 90}{5}) \\ = P (z > 2) = 1 - P (Z < 2) \\ = 1 - 0.9772 = 0.0228 \\ ∴ n u m b e r o f c a r z = 1000 \times 0.0228 = 23 c a r \end{array}$

$40$ يمكن نمذجة كتل البيض في إحدى المزارع بتوزيع طبيعي ، وسعه الحسابي 60 g ، وانحرافه المعياري 4 g .

أجد عدد البيض صغير الحجم من بين 5000 بيضة في المزرعة ، علما بأن كتلة البيضة الصغيرة لا تزيد على 55 غرامًا.

$\begin{array}{l} 40 P (x \leq 55) : X ~ N (60, {(4)}^{2}) \\ S o l u t i o n : \\ P (x \leq 55) = P (Z \leq \frac{55 - 60}{4}) \\ = P (z \leq - 1.25) = P (Z \geq 1.25) \\ = 1 - P (z \leq 1.25) \\ = 1 - 0.8944 = 0.1056 \\ ∴ n u m b e r o f e g e z = 5000 \times 0.1056 = 528 e g e \end{array}$

مهارات التفكير العليا

$41$ أكتشف الخطأ:

قالت عبير: "إذا كان : $X ~ N (6.4, 0.09)$ فإن 95 % من البيانات تقع بين 6.22 و 6.58 ".

أكتشف الخطأ في قول عبير، ثم أصححه.

$\begin{array}{l} 41 P (x \leq 55) : X ~ N (6.4, {(0.3)}^{2}) \\ S o l u t i o n : \end{array}$

تقع ما نسبته 95 % حسب القاعدة التجريبية من البيانات بين $μ+2σ , μ−2σ$ . أي أن الفترة هي :

$\begin{array}{l} [6.4 - 2 (0.3), 6.4 + 2 (0.3)] = [6.4 - 0.6, 6.4 + 0.6] \\ = [5.8, 7] \end{array}$

وسبب الخطأ أستخدام الرقم 0.09 بدل 0.3 في تعوض التباين .

تبرير: إذا كان: $,P (X > 35) = 0.025, P (X < 15) = 0.1469, X ~ N (μ, {(σ)}^{2})$ فأجد قيمة كل من $σ, μ$ . مبررا إجابتي.

$\begin{array}{l} 42 X ~ N (μ, {(σ)}^{2}) \\ S o l u t i o n : \\ P (X < 35) = P (Z < \frac{15 - μ}{σ}) = 0.1469 \\ T o f i n d z : P (Z < - z) = P (Z > z) \\ = 1 - P (Z < z) = 0.1469 \\ ∴ P (Z < z) = 0.8531 ∴ z = 1.05 f r o m t h e t a b l e \\ S o : \frac{15 - μ}{σ} = 1.05 \Rightarrow 15 - μ = - 1.05 σ . .. 1 * \\ P (X > 35) = P (Z > \frac{35 - μ}{σ}) = 0.025 \\ T o f i n d z : P (Z < z) = 1 - P (Z > z) \\ = 1 - 0.025 = 0.975 f r o m t h e t a b l e \\ ∴ P (Z < z) = 0.975 ∴ z = 1.96 \\ S o : \frac{35 - μ}{σ} = 1.96 \Rightarrow 35 - μ = 1.96 σ . .. 2 * \\ n o w s o l v i n g 1 a n d 2 : \\ 20 = 3.016 σ ∴ σ = 6.64 a n d μ = 22 \end{array}$

$43$ تبرير: تقدم 100000 طالب لاختبار دولي ، وبلغ عدد الطلبة الذين زادت علاماتهم في الاختبار على 90 % نحو 10000 طالب

منهم 5000 طالب أحرزوا علامات أكثر من 95 % . إذا كانت علامات الطلبة المتقدمين تتبع توزيعاً طبيعيًا،

فأجد الوسط الحسابي والانحراف المعياري للعلامات.

$\begin{array}{l} 43 X ~ N (μ, {(σ)}^{2}) \\ S o l u t i o n : \\ P (X > 90) = P (Z > \frac{90 - μ}{σ}) = 0.1 \\ T o f i n d z : P (Z < z) = 1 - P (Z > z) \\ = 1 - 0.1 = 0.9 \\ ∴ P (Z < z) = 0.9 ∴ z = 1.28 f r o m t h e t a b l e \\ S o : \frac{90 - μ}{σ} = 1.28 \Rightarrow 90 - μ = 1.28 σ . .. 1 * \\ P (X > 95) = P (Z > \frac{95 - μ}{σ}) = \frac{5000}{100000} = 0.05 \\ T o f i n d z : P (Z < z) = 1 - P (Z > z) \\ = 1 - 0.05 = 0.95 \\ ∴ P (Z < z) = 0.95 ∴ z = 1.64 f r o m t h e t a b l e \\ S o : \frac{95 - μ}{σ} = 1.64 \Rightarrow 95 - μ = 1.64 σ . .. 2 * \\ n o w s o l v i n g 1 a n d 2 : \\ 5 = 0.36 σ ∴ σ = 13.89 a n d μ = 72.22 \end{array}$

$44$ تحد: أجرت باحثة تفاعلا كيميائيا بصورة مُتكرّرة؛ فوجدت أن الزمن اللازم لحدوث التفاعل يتبع: توزيعا طبيعيا ،

وأن 50 % من التجارب يلزمها أكثر من 13 دقيقة لحدوث التفاعل وأنَّ 12 % منها تتطلّب أقل من 10 دقائق لحدوث التفاعل.

أقدر الوسط الحسابي والانحراف المعياري لزمن التفاعل.

$\begin{array}{l} 44 X ~ N (μ, {(σ)}^{2}) \\ S o l u t i o n : \\ P (X > 13) = P (Z > \frac{13 - μ}{σ}) = 0.05 \\ T o f i n d z : P (Z < z) = 1 - P (Z > z) \\ = 1 - 0.05 = 0.95 \\ ∴ P (Z < z) = 0.95 ∴ z = 1.64 f r o m t h e t a b l e \\ S o : \frac{13 - μ}{σ} = 1.64 \Rightarrow 13 - μ = 1.64 σ . .. 1 * \\ P (X < 10) = P (Z < \frac{10 - μ}{σ}) = 0.12 \\ T o f i n d z : P (Z < - z) = P (Z > z) \\ = 1 - P (Z < z) = 0.12 \\ = 1 - 0.12 = 0.88 \\ ∴ P (Z < z) = 0.88 ∴ z = 1.17 f r o m t h e t a b l e \\ S o : \frac{10 - μ}{σ} = - 1.17 \Rightarrow 10 - μ = - 1.17 σ . .. 2 * \\ n o w s o l v i n g 1 a n d 2 : \\ 3 = 2 . σ 81 ∴ σ = 1.07 a n d μ = 11.25 \end{array}$

تبرير: يبين الشكل المجاور منحنى التوزيع الطبيعي للمُتغيّرٌ االعشوائي X الذي وسطه الحسابي 79 ، وتباينه 144 ،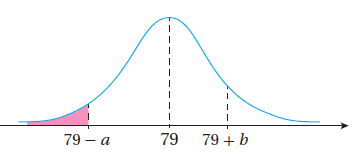

إذا كان: $P (79 - a < X < 79 + b) = 0.6463$ ، وكان: $P (X \geq 79 + b) = 2 P (X \leq 79 - a)$ .

فأجد كلا مما يأتي. مبررا إجابتي:

$45$ مساحة المنطقة المُظللة.

$\begin{array}{l} 45 X ~ N (79, {(12)}^{2}) \\ S o l u t i o n : \end{array}$

$46$ قيم الثابت b .

$\begin{array}{l} 46 X ~ N (79, {(12)}^{2}) \\ S o l u t i o n : \\ s i n c e P (X \leq 79 - a) = 0.1179 \\ ∴ P (Z < z) = 1 - 0.1179 = 0.8821 \\ ∴ z = - 1.18 f r o m t h e t a b l e \\ S o : \frac{79 - a - 79}{12} = - 1.18 \\ \Rightarrow \frac{a}{12} = 1.18 ∴ a = 14.16 \\ A_{2} = 0.2358 \\ P (X < 79 + b) = 1 - 0.2358 = 0.7642 \\ ∴ z = 0.72 f r o m t a b l e \\ S o : \frac{79 + b - 79}{12} = 0.72 \Rightarrow b = 8.64 \end{array}$

رياضيات فصل ثاني

التوجيهي علمي

Get it for

MAC

Get it for

WINDOWS