أجد المحل الهندسي الذي تُمثَّله المعادلة: ثم أكتب المعادلة بالصيغة الديكارتية.
المحل الهندسي هو دائرة نصف قطرها 7 وحدات ومركزها النقطة

أجد المحل الهندسي الذي تُمثَله المعادلة: ثم أكتب المعادلة بالصيغة الديكارتية.
الحل:
حسب التعريف فهذه معادلة المنصف العامودي للقطعة المستقيمة الواصلة بين النقطتين
الحل الآخر:
المنصف العامودي يمر بنقطة منتصف القطعة المستقيمة :
ويحقق سالب ومقلوب ميل المستقيم المار بالنقطتين بسبب التعامد
.
لذلك فمعادلة المستقيم المار بالنقطة ، وميله

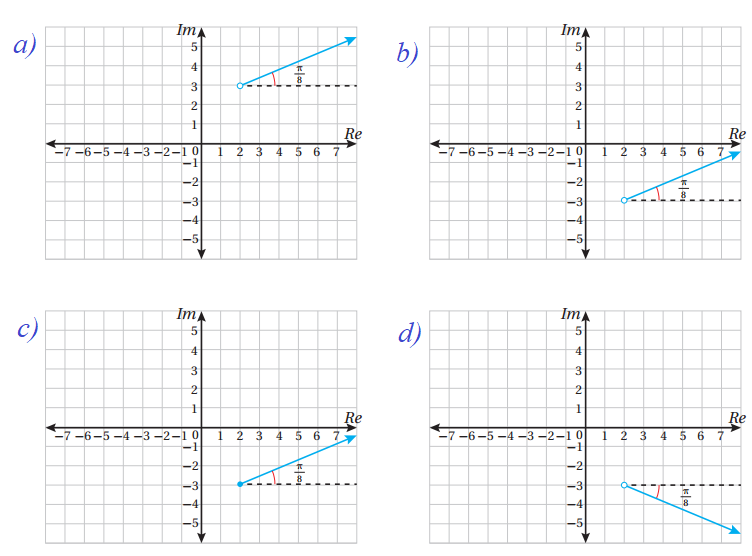
أجد المحل الهندسي الذي تُمثَّله كل معادلة ممّا يأتي ، ثم أرسمه في المستوى المُركَّب:
الحل:
حسب التعريف فهذه معادلة الشعاع الذي يبدأ من نقطة الأصل وسعته

الحل:
حسب التعريف فهذه معادلة الشعاع الذي يبدأ من النقطة ،
ويصنع زاوية قياسها مع الاتجاه الموجب لمحور

أُمثل في المستوى المُركَب المحل الهندسي للنقاط التي تُحقّقَ كل متباينة مما يأتي:
الحل:
المنحنى الناتج دائرة نصف قطرها 6 وحدات ، ومركزها النقطة ،
والمنطقة المظللة داخل وعلى حدود (محيط) الدائرة

الحل:
الشكل الناتج هو المنصف العامودي للقطعة الواصلة بين النقطتين
والذي يمثل بالمتباينة الجبرية . وباختبار العدد الذي يحقق المتباينة .
الحل:
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع محور x الموجب .
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع محور x الموجب .

أمثَل في المستوى المركَب المحل الهندسي للنقاط التي تُحقّق المتباينة:، والمتباينة:
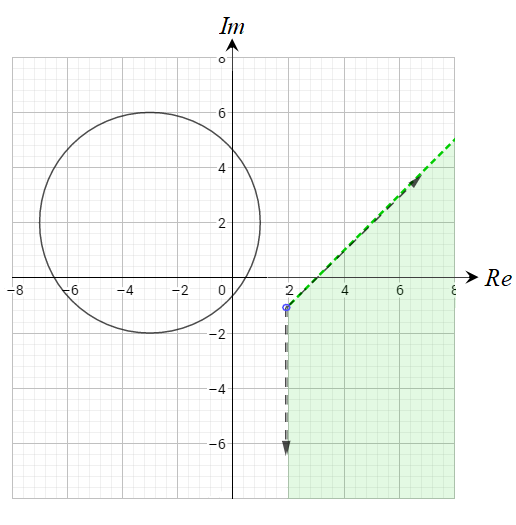 الحل:
الحل:
المنحنى الناتج دائرة نصف قطرها 6 وحدات ، ومركزها النقطة
والمنطقة المظللة خارج وعلى حدود (محيط) الدائرة .
والمنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة
ويصنع زاوية قياسها مع مستقيم يوازي محور x .
والمنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة
ويصنع زاوية قياسها مع مستقيم يوازي محور x .

أجد المحل الهندسي الذي تُمثَّله كل معادلة مما يأتي ، ثم أمثله في المستوى المركب ، ثم اجد معادلته الديكارتية .
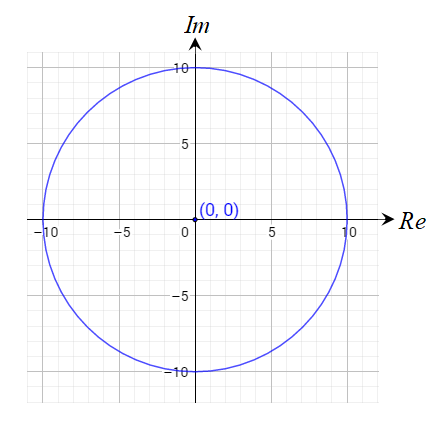
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 10 وحدات ومركزها النقطة
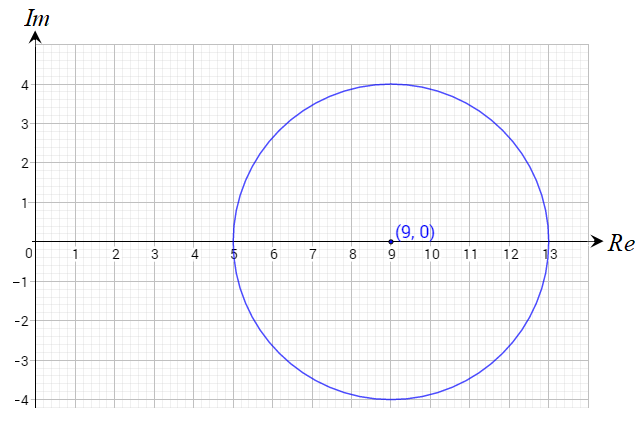
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 4وحدات ومركزها النقطة
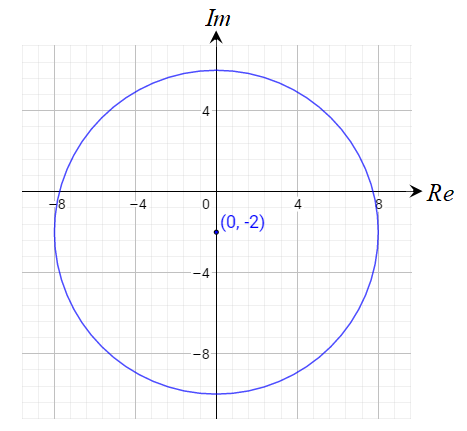
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 8 وحدات ومركزها النقطة
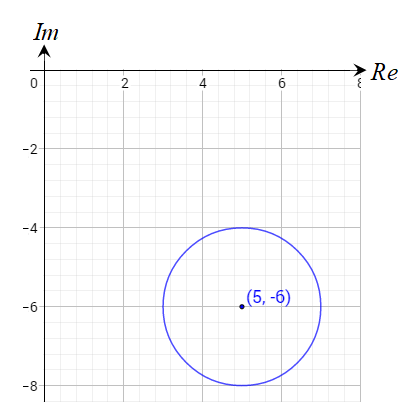
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 2 وحدة ومركزها النقطة
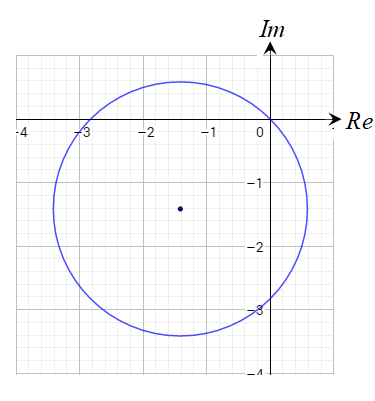
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 2 وحدة ومركزها النقطة
الحل:
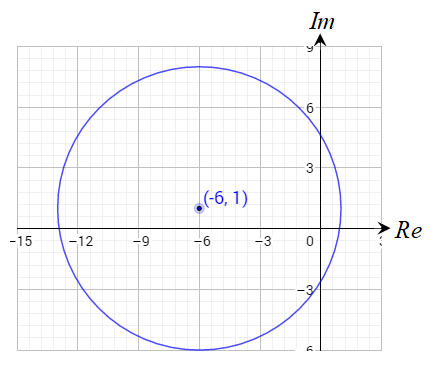
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 7 وحدات ومركزها النقطة
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة بين النقطتين
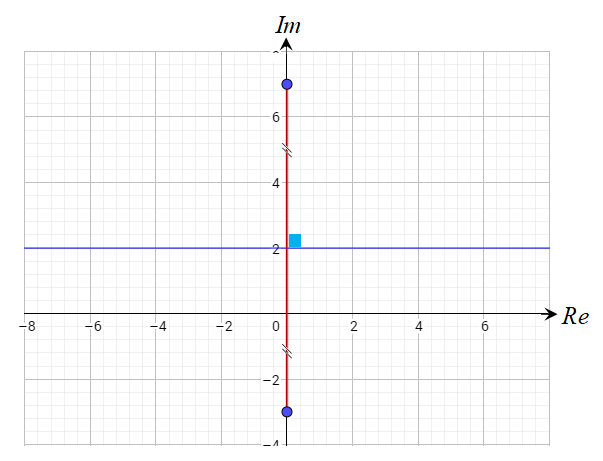
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة بين
النقطتين
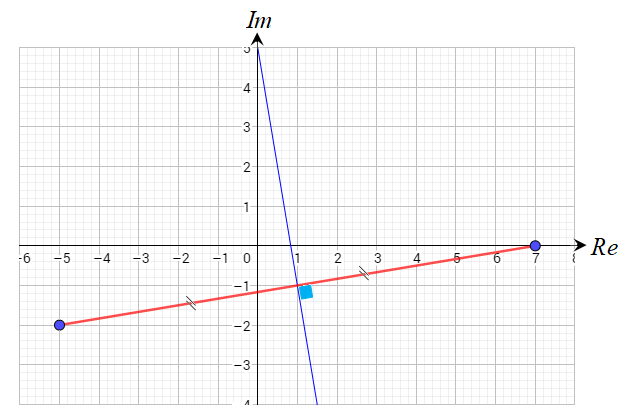
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة
بين النقطتين
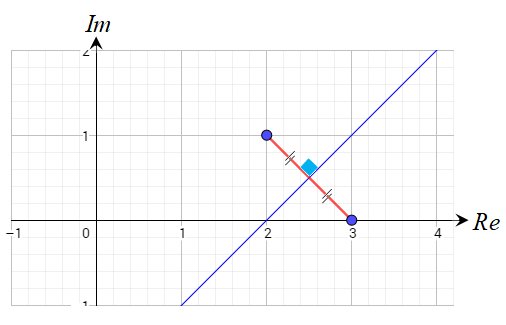
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة
بين النقطتين
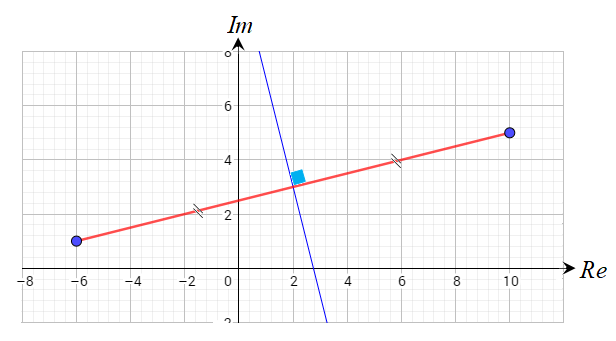
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة
بين النقطتين
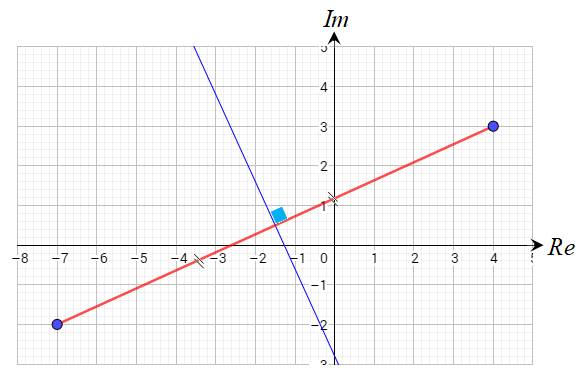
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة
بين النقطتين
أجد المحل الهندسي الذي تُمثَّله كل من المعادلات التالية ، ثم أمثله في المستوى المركب.
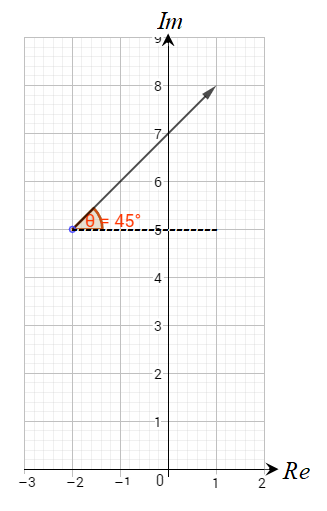
الحل:
المنحنى الناتج عن المعادلة
هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .

الحل:
المنحنى الناتج عن المعادلة
هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
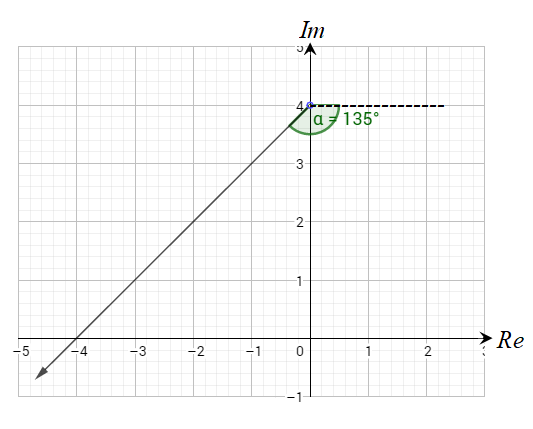
الحل:
المنحنى الناتج عن المعادلة
هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
أَمثل في المستوى المُركَّب المنطقة التي تحددها كل متباينة مما ياتي :
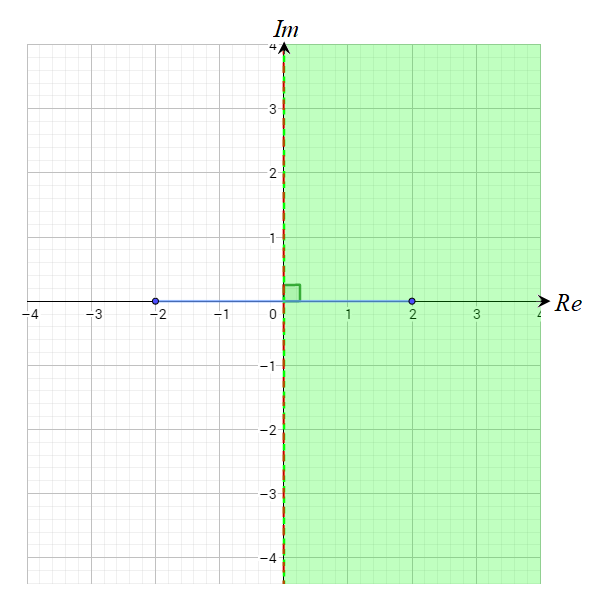
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة بين النقطتين
.
والذي يمثل بالمتباينة الجبرية . وباختبار العدد الذي يحقق المتباينة .
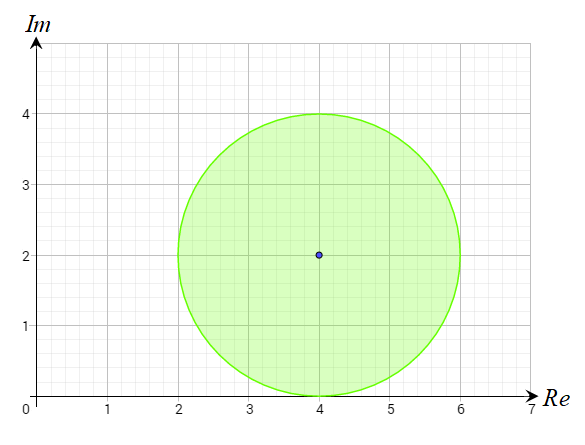
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 2 وحدة ومركزها النقطة
والذي يمثل بالمتباينة الجبرية .
وباختبار العدد الذي يحقق المتباينة .
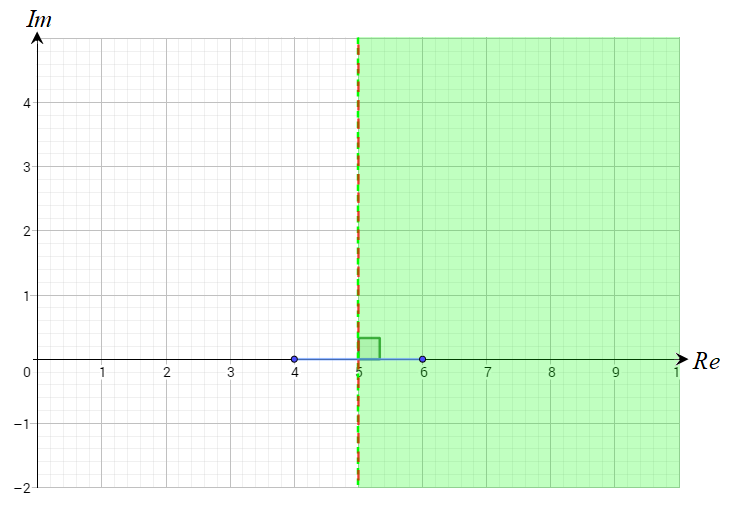
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة الواصلة بين
النقطتين .
والذي يمثل بالمتباينة الجبرية . وباختبار العدد الذي يحقق المتباينة .
الحل:
المنحنى الناتج عن المعادلة
هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
والمنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
وباختبار العدد الذي يحقق المتباينة بحيث :
الحل:
المنحنى الناتج عن المعادلة . هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم . ويكافئ المتباينة
والمنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .ويكافئ المتباينة
وباختبار العدد الذي يحقق المتباينة بحيث :
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها 4 وحدات ومركزها النقطة
والذي يمثل بالمتباينة الجبرية .
والمنحنى الناتج عن المعادلة هو دائرة نصف قطرها 2 وحدة ومركزها النقطة
والذي يمثل بالمتباينة الجبرية .
وباختبار العدد الذي يحقق المتباينة .
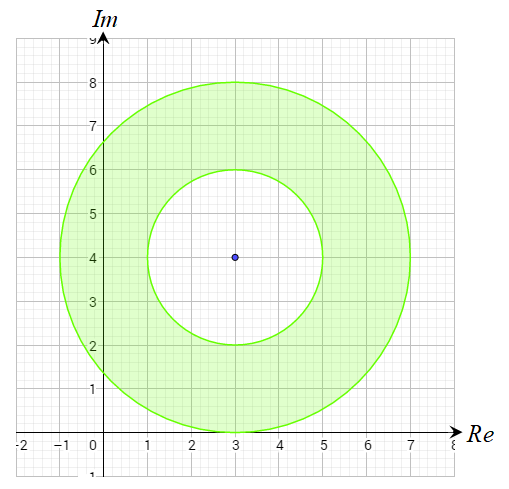
22) أَمثّل في المستوى المُركَّب نفسه المحل الهندسي الذي تُمثله كل من المعادلة:
والمعادلة: . ثم أجد الأعداد المُركّبة التي تُحقّق المعادلتين معًا.
 الحل:
الحل:
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها وحدة
ومركزها النقطة ، وتمثل جبرياً بالمعادلة .
والشكل الناتج عن المعادلة هو المنصف العامودي
للقطعة المستقيمة الواصلة بين النقطتين .
وتمثل جبرياً بالمعادلة :
لإيجاد الأعداد المُركّبة التي تُحقّق المعادلتين معًا سنحل النظام :
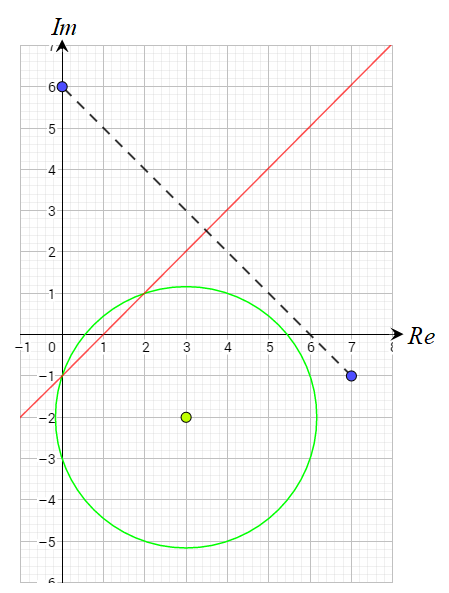
23) أجد العدد المُركَبٍ الذي يحقق كُلا من المحل الهندسي: ، والمحل الهندسي:
الحل:
سنحل المعادلتين جبرياً :
24) أَمثل في المستوى المُركَّب نفسه المحل الهندسي الذي تُمثله كلّ من المعادلات الآتية:
 الحل:
الحل:
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
المنحنى الناتج عن المعادلة هو دائرة نصف قطرها وحدات ومركزها النقطة
25) أمثل في المستوى المُركب المحل الهندسي للنقاط التي تُحقّق المتباينة:
والمتباينة: .
 الحل:
الحل:
الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة
الواصلة بين النقطتين والذي يمثل بالمتباينة الجبرية .
وباختبار العدد الذي يحقق المتباينة .
وكذلك الشكل الناتج عن المعادلة هو المنصف العامودي للقطعة المستقيمة
الواصلة بين النقطتين والذي يمثل بالمتباينة الجبرية .
وباختبار العدد الذي يحقق المتباينة .
26) أمثل في المستوى المُركَّب المحل الهندسي للنقاط التي تُحقَّق المتباينة:
والمتباينة: .
 الحل:
الحل:
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
المنحنى الناتج عن المعادلة هو دائرة متقطعة مركزها النقطة
ونصف قطرها وحدة.
27) أمثل في المستوى المُركَّب المحل الهندسي للنقاط التي تُحقَّق المتباينة:
والمتباينة: .
 الحل:
الحل:
المنحنى الناتج عن المعادلة هو شعاع متصل يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
المنحنى الناتج عن المعادلة هو شعاع متصل يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
المنحنى الناتج عن المعادلة هو دائرة متصلة مركزها النقطة ونصف قطرها وحدات .
المنحنى الناتج عن المعادلة هو دائرة متقطعة مركزها النقطة ونصف قطرها وحدة .
أكتب بدلالة z معادلة المحل الهندسي الممثل في كل مما يأتي :
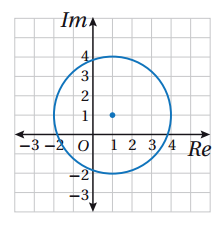
28) الحل:
المنحنى الناتج عن المعادلة
هو دائرة مركزها النقطة ونصف قطرها وحدات .
29) الحل:
الشكل الناتج المنصف العامودي للقطعة المستقيمة الواصلة بين النقطتين
ويمر بنقطة منتصف القطعة المستقيمة :
ويحقق سالب ومقلوب ميل المستقيم بسبب التعامد .
لذلك فمعادلة المستقيم المار بالنقطة ، وميله هي :
لذلك فمعادلة المستقيم هي :
الحل الآخر:
باعتماد أن كل نقطة في المستوى المركب تمثل عدداً مركباً فإن :
بالتالي فإنَّ معادلة المنصف العامودي تعطى بالعلاقة :
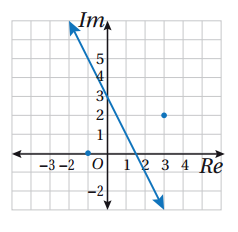
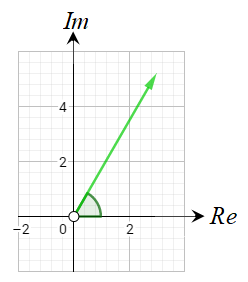
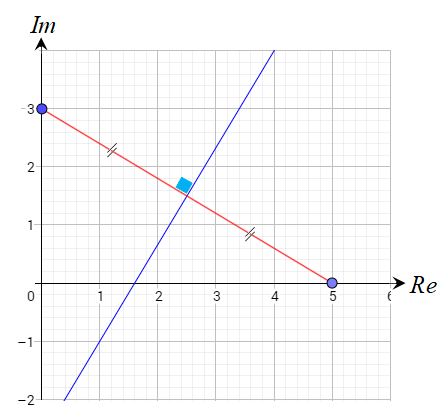
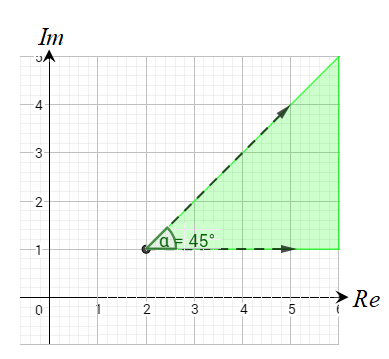
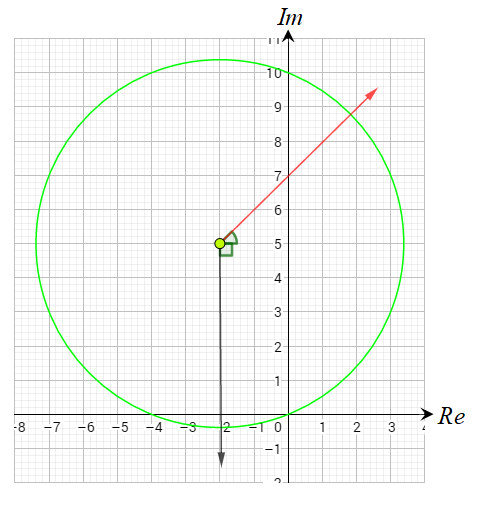
30) أكتب معادلة في صورة: حيث a عدد مركب
و تمثل المحل الهندسي المبيّن في الشكل المجاور.
الحل :
المنحنى الناتج هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم .
بالتالي فإنَّ المعادلة هي :
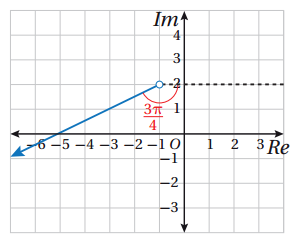
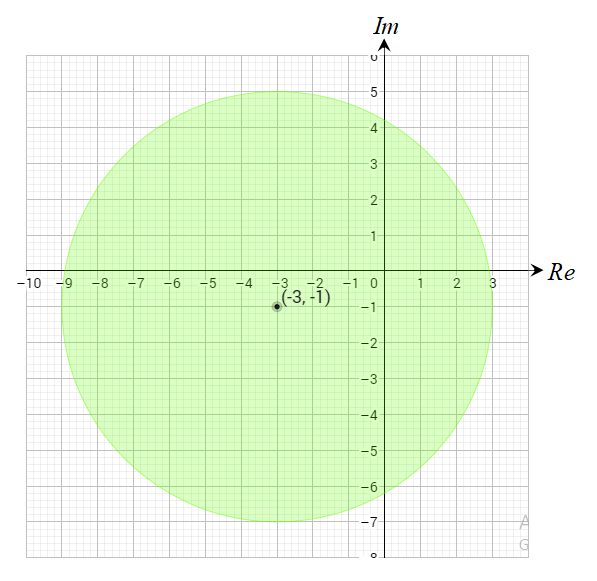
أكتب (بدلالة z) متباينة المحل الهندسي الذي تمثله المنطقة المظللة في كل مما يأتي :
31) الحل :
المنطقة المظللة الناتجة هي خارج الدائرة المتصلة مركزها النقطة وتمر بالنقطة
ونصف قطرها .
ومعادلته هي : .
32) الحل :
المنطقة المظللة الناتجة تقاطع الشعاعين :
الشعاع الذي يبدأ من النقطة ، ولا يشملها . ويصنع زاوية قياسها مع المستقيم .
فالمعادلة هي وذلك باختبار نقطة الأصل
الشعاع الذي يبدأ من النقطة ، ولا يشملها . ويصنع زاوية قياسها مع المستقيم .
فالمعادلة هي وذلك باختبار نقطة الأصل .
والمهم الآن كيف حسبت زاوية المستقيم :
بإعتماد نقطتين على المستقيم مثل
فالمتباينة :
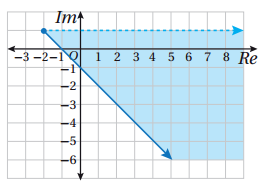
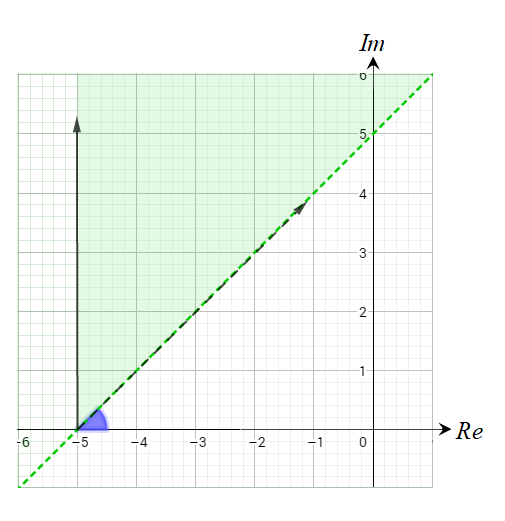
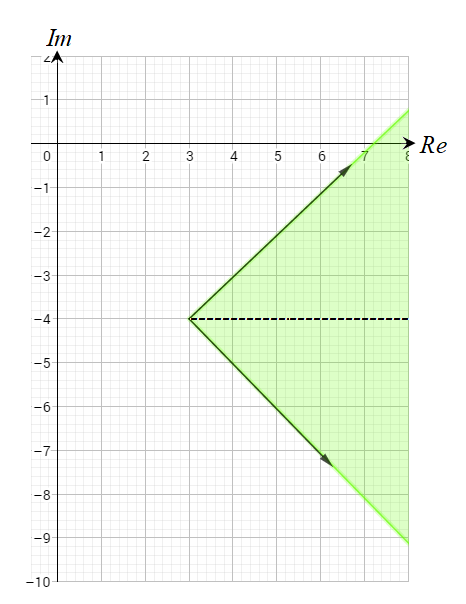
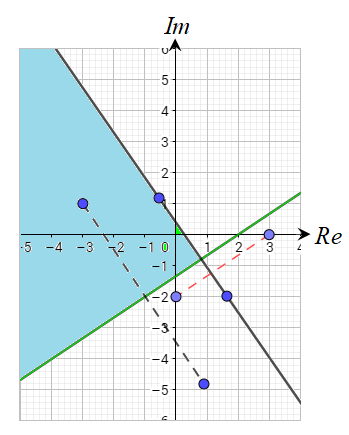
33) أكتب (بدلالة z) نظام متباينات يُمثَل المحل الهندسي المٌبيِن في الشكل المجاور.
الحل :
المنطقة المظللة الناتجة تقاطع المنحنيين :
المنطقة المظللة الناتجة هي داخل الدائرة المتصلة مركزها النقطة ونصف قطرها 3 وحدات .
ومتباينتها هي .
والمنطقة المظللة الناتجة هي دون الخط المستقيم (المنصف العامودي) المتصل بين النقطتين
ومتباينته هي :
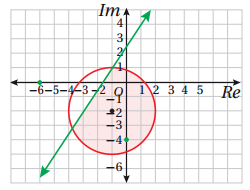
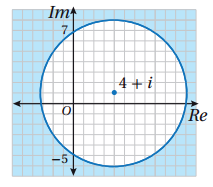
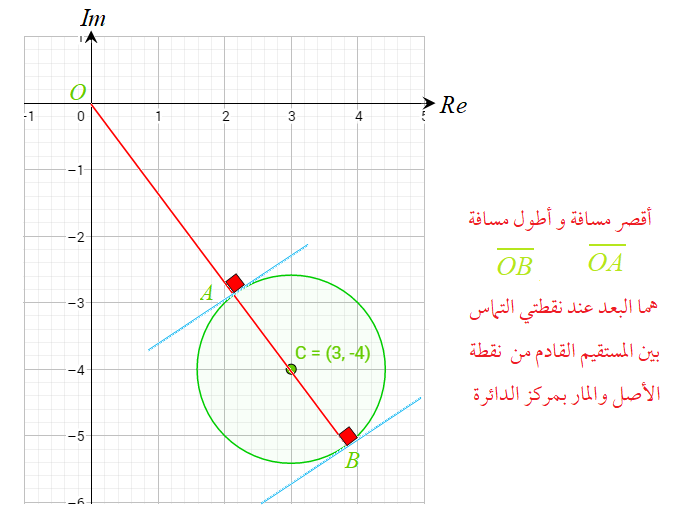
34) تبرير : إذا كان العدد المركب z يحقق المعادلة : فأجد اكبر قيمة لــِ وأقل قيمة له . مبرراً إجابتي .
الحل :
المنحنى الناتج عن المعادلة يمثل دائرة ، مركزها النقطة ونصف قطرها وحدتان .
و Z هي مجموعة النقط التي تحقق معادلة الدائرة ( واقعة عليها) .
ويقع أقصر وأطول بعد عند نقطتي التماس مع المستقيم المار بنقطتي التماس والمرسوم من نقطة الاصل :
35) تحدٌ: أثبت أن المعادلة تمثل دائرة ، ثم أجد مركزها ونصف قطرها .
الحل :
المنحنى الناتج عن المعادلة يمثل دائرة :
36) تبرير: أي الآتية هو المحل الهندسي الذي معادلته: مبرراً إجابتي
الحل:
المنحنى الناتج عن المعادلة هو شعاع يبدأ من النقطة ، ولا يشملها .
ويصنع زاوية قياسها مع المستقيم . فالتمثيل الصحيح هو الشكل b .