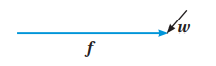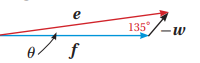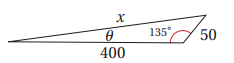رياضيات

جمع المتجهات وطرحها 

• المتجهان المتساويان :

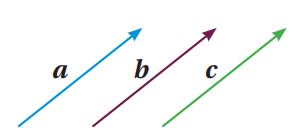
هما متجهان لهما نفس الاتجاه والمقدار. كما في الشكل أدناه 

المتجهات a , b , c  متساوية و بالرموز  a =b = c 

• المتجهان المتوازيان

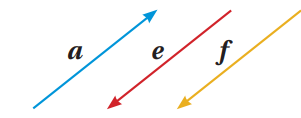
هما متجهان لهما الاتجاه نفسه أو عكسه ولس شرطا أن يكون لها المقدار نفسه 

كما في الشكل أدناه 

المتجهات  a , e , f متوازية  وبالرموز $a \overline{)\overline{) e \overline{)\overline{) f}}}}$

 

• معكوس المتجه 

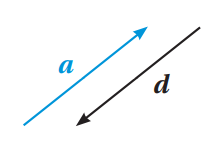
هو متجه له نفس مقدار متجه آخر ، لكنه في اتجاه معاكس له . كما في الشكل أدناه 

المتجه d معكوس المتجه a  وبالرمز   a -  أي أن  d = - a 

مثال

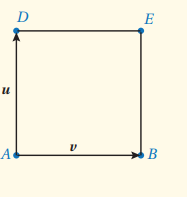
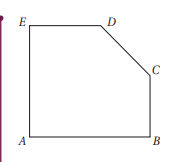
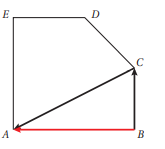
في الشكل المجاور  ABED مربع  ، فيه $\stackrel{\mathbf{\rightharpoonup }}{\mathbf{AD}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{u}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{AB}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{v}$  ،   أعبر  عن كل من $\stackrel{\mathbf{\rightharpoonup }}{\mathbf{E}\mathbf{B}}$  و $\stackrel{\rightharpoonup }{\mathit{D}\mathit{E}}$   باستعمال      المتجهين  v , u 

 

الحل 

$\stackrel{\mathbf{\rightharpoonup }}{\mathbf{EB}}$

 متجه موازٍ  و معكوس للمتجه $\stackrel{\rightharpoonup }{\mathit{A}\mathit{D}}$

إذا 

$\stackrel{\mathbf{\rightharpoonup }}{\mathbf{E}\mathbf{B}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{ }\mathit{u}$

 

$\stackrel{\mathbf{\rightharpoonup }}{\mathbf{D}\mathbf{E}}$

متجه موازٍ و مساوٍ للمتجه $\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{B}}$

إذا 

$\stackrel{\mathbf{\rightharpoonup }}{\mathbf{D}\mathbf{E}}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{v}$

---

جمع المتجهات هندسيًا 

يمكن إيجاد ناتج جمع متجهين أو أكثر هندسيًا . 

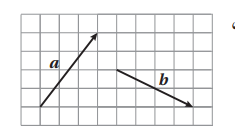
خطوات إيجاد a + b  هندسيا 

الخطوة 1  : ارسم المتجه a 

الخطوة 2 : ارسم المتجه b حيث تكون نقطة بدايته هي نقطة  نهاية المتجه a 

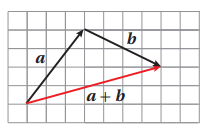
الخطوة 3 : صل بين نقطة بداية المتجه a  ونقطة نهاية المتجه b فيكون المتجه الناتج هو المتجه  a+ b 

يسمى المتجه الناتج من جمع المتجهين أو أكثر المحصلة 

 

مثال 

اعتمادًا على الشكل الآتي ، أكتب المتجه الذي يمثل ناتج الجمع في كل مما يأتي : 

 

$$\begin{gathered} \mathbf{1}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{ }\mathbf{B}\mathbf{C}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{A}\mathbf{ }} \\ \stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{A}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{A}} \end{gathered}$$

هنا نصل بداية $\stackrel{\rightharpoonup }{BC}$  بنقطة نهاية $\stackrel{\rightharpoonup }{CA}$  ينتج $\stackrel{\rightharpoonup }{BA}$

 

$$\begin{gathered} \mathbf{2}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{A}}\mathbf{ }\mathbf{+}\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{E}}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{E}\mathbf{C}} \\ \stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{A}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{E}}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{E}\mathbf{C}}\mathbf{ }\mathbf{=}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{EC}}\mathbf{ }\mathbf{نهاية}\mathbf{ }\mathbf{بنقطة}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{BA}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{بداية}\mathbf{ }\mathbf{نقطة}\mathbf{ }\mathbf{نصل}\mathbf{ } \\ \mathbf{3}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{B}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{D}\mathbf{ }}\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{D}\mathbf{E}}\mathbf{ } \\ \stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{B}}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{D}}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{D}\mathbf{E}}\mathbf{ }\mathbf{=}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{E}} \\ \mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{DE}}\mathbf{ }\mathbf{ }\mathbf{نهاية}\mathbf{ }\mathbf{بنقطة}\mathbf{ }\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{AB}}\mathbf{ }\mathbf{ }\mathbf{بداية}\mathbf{ }\mathbf{ }\mathbf{نقطة}\mathbf{ }\mathbf{نصل}\mathbf{ } \\ \mathbf{4}\mathbf{.}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{B}}\mathbf{ }\mathbf{+}\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}}\mathbf{ }\mathbf{+}\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{A}} \\ \stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{B}}\mathbf{ }\mathbf{+}\stackrel{\mathbf{\rightharpoonup }}{\mathbf{B}\mathbf{C}}\mathbf{ }\mathbf{+}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{C}\mathbf{A}}\mathbf{ }\mathbf{=}\mathbf{ }\stackrel{\mathbf{\rightharpoonup }}{\mathbf{A}\mathbf{A}} \end{gathered}$$

 

---

طرح المتجهات هندسيًا 

يمكن إيجاد ناتج طرح متجهين أو أكثر هندسيًا .

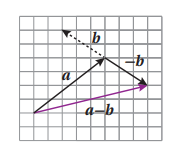
لإيجاد a -b  نجمع المتجه a  مع معكوس المتجه b أي 

a  - b = a +  ( -b )

و لذلك يمكن إيجاد ناتج طرح  a- b  هندسيا بطريقة مشابهة لعملية الجمع كما في الشكل الآتي : 

ثم نجد محصلة  a و   b - 

---

ضرب المتجه في عدد ثابت هندسيًا

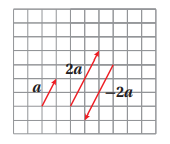
ينتج من ضرب المتجه a  في العدد الحقيقي k  متجه موازٍ للمتجه a  ويكون للمتجهين  ka  و a  الاتجاه نفسه إذا كان k  عددا موجبا  و اتجاهان متعاكسان إذا كان  k  عددًا سالبًا . 

 2 a = a +a 

-2a  = -a + ( -a ) 

 

مثال 

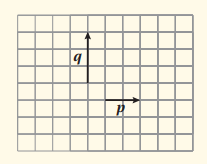
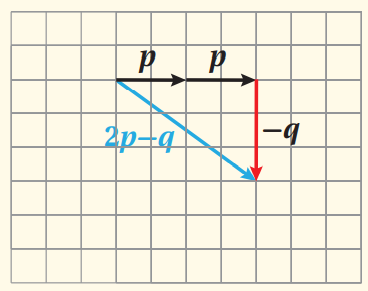
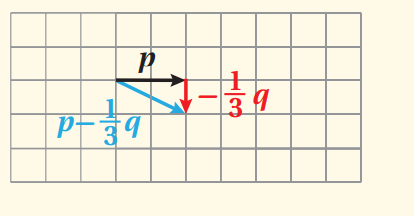
اعتمادًا على الشكل المجاور ، أجد هندسيًا كلا مما يأتي : 

 1.  2p -  q 

نرسم المتجه  2q   , والمتجه  q - 

ثم نجد محصلة المتجهتين 

 

2. p  - $\frac{1}{3}q$

نرسم المتجه  p  , والمتجه  q$\frac{1}{3}$ - 

ثم نجد محصلة المتجهتين 

 

---

جمع المتجهات وطرحها وضربها في ثابت جبريًا 

يمكن إيجاد ناتج الجمع والطرح والضرب في ثابت للمتجهات المكتوبة بالصورة الإحداثية عن طريق جمع مركباتها الأفقية و الرأسية ، أو طرحها .

 

مفهوم أساسي 

إذا كان   و   وكان k عددًا حقيقيًا ، فإن : 

$$\begin{gathered} \mathit{a}\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }\mathit{b}\mathbf{=}< x_1 + x_2 , y_1 + y_2> \\ \mathit{a}\mathbf{ }\mathbf{-}\mathbf{ }\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }< x_{1 }- x_2 , y_1 - y_2> \\ \mathit{k}\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }<k x_1 , k x_2> \end{gathered}$$

 

مثال 

إذاكان  فأجد كل مما يأتي 

$$\begin{gathered} \mathbf{1}\mathbf{.}\mathbf{ }\mathit{a}\mathbf{ }\mathbf{+}\mathit{b}\mathbf{ } \\ \mathit{a}\mathbf{+}\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }<3 + (-4) , 1+6>\mathbf{ }\mathbf{=}\mathbf{ }<-1 , 7> \\ \mathbf{2}\mathbf{.}\mathbf{ }\mathbf{2}\mathit{a}\mathbf{ } \\ \mathbf{2}\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }<2 \left(3\right) , 2\left(1\right) >\mathbf{=}\mathbf{ }<6 , 2> \\ \mathbf{3}\mathbf{.}\mathbf{ }\mathit{c}\mathbf{ }\mathbf{-}\mathbf{ }\mathit{b} \\ \mathit{c}\mathbf{-}\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }<-3 - (-4) , -1 -6>\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }<1 , -7> \\ \mathbf{4}\mathbf{.}\mathbf{ }\mathit{a}\mathbf{ }\mathbf{+}\mathit{c}\mathbf{ } \\ \mathit{a}\mathbf{ }\mathbf{+}\mathit{c}\mathbf{ }\mathbf{=}\mathbf{ }<3 + (-3) , 1 +(-1)>\mathbf{ }\mathbf{=}\mathbf{ }<0 , 0> \end{gathered}$$

 

---

لجمع المتجهات وطرحها تطبيقات في مجالات عدة ، مثل الهندسة و الطيران

 

مثال من الحياة 

ملاحة جوية : بدأت طائرة رحلتها نحو الشرق بسرعة مقدارها  400km / h   لكنها واجهت رياحا تهب من الشمال الشرقي بسرعة 50km / h .  كيف يمكن لربان الطائرة أن يعدل مقدار سرعتها و اتجاهها ليصل إلى وجهته من دون تأخير ؟ 

 

الحل 

نرسم المتجهين اللذين يمثلان السرعة و الاتجاه لكل من الطائرة والرياح . 

يمثل المتجه f  السرعة المتجهة للطائرة ويمثل  المتجه w  السرعة المتجهة للرياح 

نلاحظ من الشكل الآتي أنه يجب على الطائرة أن تنحرف عن مسارها قليلا بحيث تعيدها الرياح إلى مسارها الأصلي . 

ثم نرسم المتجه الذي يمثل السرعة المتجهة للطائرة بعد انحرافها عن مسارها . 

بما أن الرياح تهب من الشمال الشرقي فإن اتجاه w  هو $45°$ لذا فإن الزاية بين f  و W  تساوي $135°$ 

ويكون المتجه e  هو محصلة المتجهين f  و w - 

 ثم نحدد سرعة الطائرة بعد انحرافها 

مقدار سرعة الطائرة بعد انحرافها عن مسارها يساوي مقدار المتجه e  وليكن x 

 نجد طول x  باستعمال قانون جيب التمام 

$$\begin{gathered} a^{2 } = b^2 + c^2 - 2bc cosA \\ {x}^2 = {400}^2 +{50}^2 - 2 \left(400\right)\left(50\right) cos 135° = 190784.3 \\ x\approx 436.8 \end{gathered}$$ 

 نجد  قياس زاوية انحراف الطائرة $\theta$ باستعمال قانون الجيوب 

$$\begin{gathered} \frac{sin C}{c} = \frac{sin A}{a} \\ \frac{sin \theta }{50} = \frac{sin 135°}{436.8} \\ \theta = si{n}^{-1} ( 0.0809) \approx 4.64° \end{gathered}$$

 

إذا يجب على الربان أن يحرف مسار الطائرة بزاوية $4.64°$ شمال الشرق   ويزيد مقدار سرعتها إلى 436.8km/ h  عندئذ ستعمل الرياح على تقليل مقدار سرعتها إلى  400km / h 

---