رياضيات

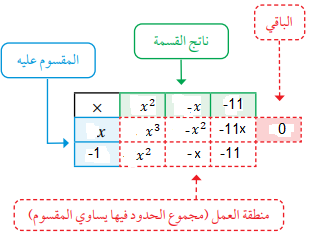
أتذكر أن الصورة العامة لكثيرات الحدود هي $a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_1 x+a_0$ حيث n عدد صحيح غير سالب، و $a_n,a_{n-1},...,a_1,a_0$ أعداد حقيقية، وأن الاقتران على الصورة $p\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_1 x+a_0$ يسمى اقتران كثير حدود، ويمكننا أيضا قسمة كثير حدود  على آخر باستعمال القسمة الطويلة.

في هذا الدرس سنتعرف على طريقة جديدة لقسمة كثيرات الحدود تعتمد بشكل أساسي على ضرب كثيرات الحدود كعملية عكسية لعملية القسمة.

مثال:

استعمل طريقة الجدول لأجد ناتج $\left(2x^3-x^2+4\right)÷(x+2)$ وأتحقق من صحة الحل:

1) ننشئ جدول من أربع أعمدة (درجة ناتج القسمة +2)وثالثة صفوف (درجة المقسوم عليه +2)، ثم نكتب حدود المقسوم عليه في العامود الأيسر، ونضيف خانة الباقي إلى منطقة العمل.

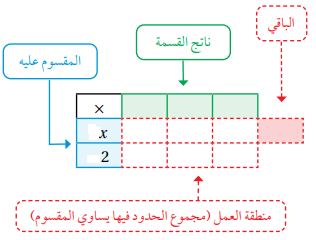
2) نكتب الحد الرئيس من المقسوم ($2x^3$) في الخانة اليسرى العليا من منطقة العمل

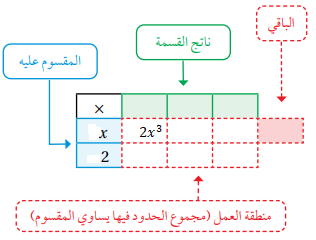
3) نبحث عن حد جبري ناتج ضربه في x يساوي $2x^3$ (الحد هو $2x^2$) ونكتبه أعلى الجدول

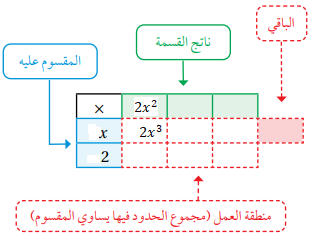
4) نضرب ($2x^2$) في 2 ونكتب الناتج ($4x^2$) في الخانة المناظرة للحدين المضروبين، وللحصول على الحد ذي الدرجة الثانية في المقسوم ($-x^2$) يجب إضافة ($-5x^2$) إلى ($4x^2$) في منطقة العمل حيث أن إضافة الحد ($-5x^2$) يحدد الحد الثاني من ناتج القسمة وهو ($-5x$) لأن ناتج ضرب ($-5x$) في (x) يساوي ($-5x^2$) .

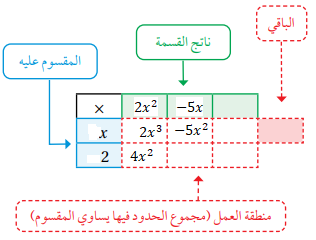
5) نضرب (5x-) في (2) ونكتب (10x-) في منطقة العمل، وبما أنه لا يوجد حد من الدرجة الأولى في المقسوم نضيف (10x) إلى منطقة العمل كي أحذف الحد (10x-) حيث إن إضافة (10x) إلى منطقة العمل يحدد الحد الأخير في ناتج القسمة وهو (10) لأن ناتج ضرب (10) في (x) يساوي (10x).

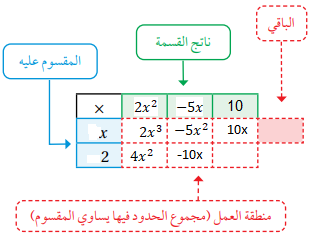
6) نضرب (10) في (2) ونكتب الناتج (20) في الخانة المتبقية من منطقة العمل وبما أنني لم أحصل على قيمة مساوية للحد الأخير (الثابت)في المقسوم فهذا يعني أنني بحاجة إلى إضافة العدد (16-) في خانة الباقي لأن ناتج جمعه إلى العدد (20) يساوي (4) وهو الحد الأخير (الثابت) في المقسوم وعندئذ يكون باقي القسمة (16-)

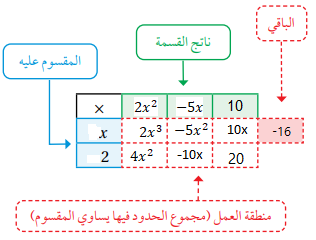
إذن، ناتج القسمة هو $2x^2-5x+10$، الباقي هو  16-، ويمكنني كتابة ذلك كما يأتي:

$\frac{2x^3-x^2+4}{x+2}=2x^2-5x+10+\frac{-16}{x+2}$

7) نتحقق من صحة الحل بإيجاد مجموع الحلول في منطقة العمل والتحقق من مساواتها للمقسوم 

$2x^3-5x^2+4x^2-10x+10x+20-16=2x^3-x^2+4$

نظرية الباقي:

باقي قسمة كثير الحدود p(x) على (x-c) هو p(c) وبصورة عامة؛ فإن باقي قسمة p(x) على (ax-b) هو $p\left(\frac{b}{a}\right)$، حيث $a\ne 0$.

مثال:

استعمل نظرية الباقي لأجد باقي قسمة p(x) على h(x) في كل مما يأتي:

$1) p(x)=x^2-2x+3 , h(x)=x+1$

باقي قسمة p(x) على h(x)=x+1 هو p(-1)

$p(-1)={(-1)}^2-2(-1)+3=6$

$2) p(x)=x^3-4x^2+3 , h(x)=x-2$

باقي قسمة p(x) على h(x)=x-2 هو p(2)

$p\left(2\right)={\left(2\right)}^3-4{\left(2\right)}^2+3=-5$

$3) p(x)=2x^3+x^2-x-1 , h(x)=2x+1$

باقي قسمة p(x) على h(x)=2x+1 هو $p(-\frac{1}{2})$

$p(-\frac{1}{2})=2{(-\frac{1}{2})}^3+{\left(-\frac{1}{2}\right)}^2-\left(-\frac{1}{2}\right)-1=\frac{-3}{2}$

نظرية العوامل:

يكون (x-c) عاملا من عوامل p(x) إذا وفقط إذا كان p(c)=0. وبصورة عامة: يكون (ax-b) عاملا من عوامل p(x) إذا وفقط إذا كان $p\left(\frac{b}{a}\right)=0$ حيث$a\ne 0$.

ملاحظة: إذا علم أحد عوامل كثير الحدود فإنه يمكننا تحليله تحليلا كاملا وذلك بكتابته على صورة حاصل ضرب مجموعة من كثيرات الحدود التي لا يمكن تحليلها (من الدرجة 1 أو من الدرجة 2 وليس لها أصفار). 

مثال:

إذا كان $p\left(x\right)=x^3+7x^2-6x-2$ 

1) أبين أن x-1 عامل  من عوامل p(x) 

يكون x-1 عاملا من عوامل p(x) إذا كان p(1) = 0 لذا أجد p(1)

$p\left(1\right)={\left(1\right)}^3+7{\left(1\right)}^2-6\left(1\right)-2=0$

إذن، x-1 هو أحد عوامل p(x).

2) أحلل p(x) تحليلاً كاملاً

بما أن x-1 إحدى عوامل p(x) فإنه يمكن إيجاد العوامل الأخرى بقسمة p(x) على x-1 ثم تحليل كثير الحدود الناتج إن أمكن.

$$\begin{gathered} p\left(x\right)=x^3+7x^2-6x-2 \\ =(x-1)(x^2+8x+2) \\ (x-1)(x-4+\sqrt{14})(x-4-\sqrt{14}) \end{gathered}$$

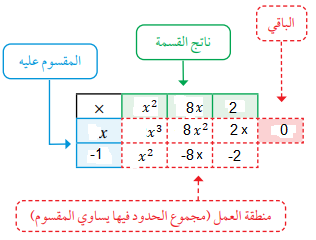
الأصفار النسبية:

تعلمنا سابقاً أن أصفار كثير الحدود هي قيم x التي يكون عندها p(x)=0 وإذا مثل الاقتران بيانياً فإن أصفاره  هي إحداثيات x لنقاط تقاطع منحناه مع المحور x وبناءً على ذلك

سنتعرف على نظرية الأصفار النسبية التي تساعدنا على إيجاد بعض الأصفار المحتملة لكثيرات الحدود لاختبارها.

نظرية الأصفار النسبية

إذا كان $p\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_{1}x+a_0$ كثير حدود معاملاته أعداد صحيحة؛ فإن كل صفر نسبي ل p(x) يكون على الصورة $\frac{p}{q}$، حيث p أحد عوامل الحد الثابت $\left(a_0\right)$، و q أحد عوامل المعامل الرئيس $\left(a_n\right)$. نتيجة من نظرية الأصفار النسبية إذا كان $a_n=1$؛ فإن كل صفر نسبي ل p(x) يكون أحد عوامل الحد الثابت $\left(a_0\right)$.

ملاحظة: يمكننا إيجاد الأصفار الأخرى من خلال استعمال القسمة الطويلة والتحليل.

مثال: أجد أصفار كثير الحدود $p\left(x\right)= 3x^3-x^2+2x-4$ جميعها.

بيانيا: يمكننا أن نستعمل برمجية جيوجيبرا لتمثيل P(X) بيانيا ونحدد عدد أصفاره ونلاحظ أن p(x) يقطع محور x في نقطة واحدة أي أن له صفر واحد فقط.

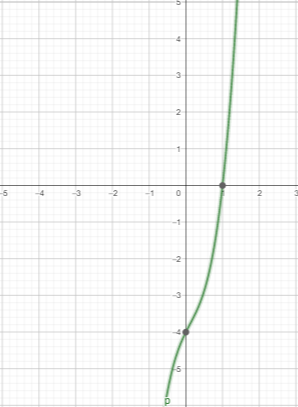
جبريا: 1) نجد الأصفار النسبية المحتملة (نجد عوامل الحد الثابت)  $\pm 1,\pm 2,\pm 4$ ثم نجد عوامل المعامل الرئيس ($\pm 1 , \pm 3$) إذن الأصفار النسبية المحتملة ($\pm 1 ,\pm \frac{1}{3} ,\pm 2 ,\pm \frac{2}{3} ,\pm 4 ,\pm \frac{4}{3}$) .

2) نختبر الأصفار النسبية بتعويضها بالاقتران p(x) ونأخذ العوامل التي يكون ناتج تعويضها يساوي صفر، فيكون العامل الوحيد هو x-1.

3) نحلل كثير الحدود تحليلا كاملا وبما أن x-1 هو عامل من عوامل p(x) يمكننا إيجاد العوامل الأخرى بقسمة p(x) على x-1 ثم تحليل كثير الحدود الناتج إن أمكن

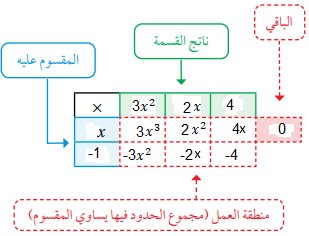
حل معادلات كثيرات الحدود

المعادلة التي يمكن كتابتها على صورة $p\left(x\right)=0$ حيث p(x) كثير حدود من أي درجة تسمى معادلة كثير الحدود التي يمكن حل البعض منها باستخدام طرائق التحليل البسيطة كإخراج عامل مشترك أو بالتجميع ونستعمل نظرية للأصفار النسبية لحل معادلات كثيرات الحدود التي لا يمكن حلها باستعمال هذه الطرائق

مثال: أحل المعادلة $x^3- 12 x - 11=0$

كثير الحدود المرتبط في المعادلة هو $p\left(x\right)=x^3-12x-11$ حيث يكون حل المعادلة هو أصفار الاقتران المرتبط في المعادلة إذن نحتاج إلى إيجاد أصفار الاقتران

من خلال الأصفار النسبية المحتملة للاقتران نجد أن x+1 هو أحد عوامل الاقتران p(x) .

$$\begin{gathered} p\left(x\right)=(+1)(x^2-x-11) \\ (x-1)(x+\frac{1-3\sqrt{5}}{2})(x+\frac{1+3\sqrt{5}}{2}) \end{gathered}$$