أتحقق من فهمي
ص: 106
استعمل طريقة الجدول؛ لأجد ناتج كل مما يأتي:
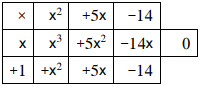
ناتج القسمة هو ، والباقي 0
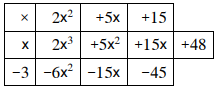
ناتج القسمة هو ، والباقي 48
أتحقق من فهمي
ص: 109
أستعمل نظرية الباقي؛ لأجد باقي قسمة P(x) على h(x) في كل مما يأتي:
الباقي هو
الباقي هو
الباقي هو
أتحقق من فهمي
ص: 110
إذا كان
a) أبين أن x-5 عامل من عوامل p(x).
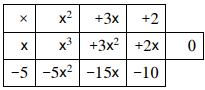
إذن، (x-5) عامل من عوامل p(x).
b) أحلل P(x) تحليلا كاملا.
لتحليل p(x) أقسم p(x) على (x-5)
أتحقق من فهمي
ص: 113
أجد أصفار كثيرات الحدود الآتية جميعها:
عوامل الحد الثابت هي ، وعوامل المعامل الرئيس هي ، و ، الأصفار المحتملة للاقتران هي: ،
بالتعويض نجد أن
إذن، (x-1) هو أحد عوامل p(x)، أجد العوامل الأخرى بالقسمة وتحليل الناتج إن أمكن.
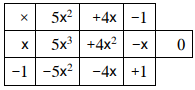
إذن، أصفار p(x) هي:
معامل الحد الرئيس يساوي 1، فالأصفار المحتملة هي عوامل الحد الثابت 8، وهي: بالتعويض نجد أن
إذن، (x-1) هو أحد عوامل Q(x)
أجد العوامل الأخرى بالقسمة وتحليل الناتج إن أمكن.
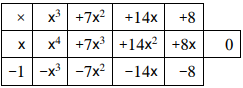
وبتعويض x = -1 في العامل التكعيبي نجد أن الناتج 0 ، نقسم على (x+1)
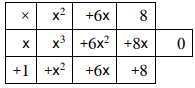
فنجد أن:
إذن، أصفار Q(x) هي:
أتحقق من فهمي
ص: 115
أحل كل معادلة مما يأتي:
حلول هذه المعادلة هي x = 1، x = -2، ويمكن حلها بتحليل الطرف الأيسر إلى عوامل بطريقة مشابهة لحل الفقرة a.
أتحقق من فهمي
ص: 116
يزيد ارتفاع أسطوانة 5cm على طول نصف قطر قاعدتها. إذا كان حجم الأسطوانة ؛ فما طول نصف قطر قاعدتها وارتفاعها؟
نصف قطر قاعدة الأسطوانة 3cm وارتفاعها 8cm
أتدرب وأحل المسائل
أستعمل طريقة الجدول؛ لأجد ناتج القسمة والباقي في كل مما يأتي:
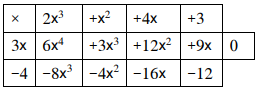
الناتج:
الباقي: 0
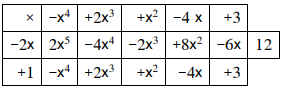
الناتج:
الباقي: 12
أستعمل نظرية الباقي؛ لأجد باقي قسمة f(x) على h(x) في كل مما يأتي:
الباقي هو:
الباقي هو:
أبين أن h(x) عامل من عوامل f(x) في كل مما يأتي:
إذن، (x+7) عامل من عوامل f(x).
إذن، (2x-3) عامل من عوامل f(x).
أحلل كل اقتران مما يأتي تحليلا كاملا:
أحل كلا من المعادلات الآتية:
15) يمثل الاقتران حجم متوازي المستطيلات المجاور. أكتب كثير حدود بالصورة القياسية يمثل المساحة الكلية لسطح متوازي المستطيلات.
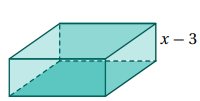
مساحة السطح الكلية = المساحة الجانبية + 2 × مساحة القاعدة
أستعمل التمثيل البياني لمنحنى كل اقتران مما يأتي؛ لإيجاد أحد أصفاره النسبية، ثم أجد أصفار الاقتران جميعها:
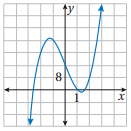
أحد أصفار الاقتران هو x = 1
صفراه الآخران هما جذرا المعادلة:
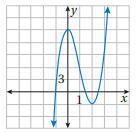
أحد أصفار الاقتران هو x = -1
صفراه الآخران هما جذرا المعادلة:
18) إذا كان x=1 , x=4 هما حلان للمعادلة ، فأجد الحل الثالث لها.
معامل :
إذن، الحل الثالث هو x= -2
19) إذا كان باقي قسمة على x-1 يساوي مثلي باقي قسمته على x+1، فما قيمة a؟
20) منحوتات جليدية: تصنع بعض المنحوتات الجليدية عن طريق ملء قالب بالماء ثم تجميده. إذا كانت إحدى المنحوتات الجليدية على شكل هرم قاعدته مربعة الشكل، وارتفاعها يزيد 1m على طول قاعدتها، أجد أبعاد المنحوتة إذا كان حجمها
المعادلة ليس لها حل لأن مميزها (15-)، فالحل الوحيد للمعادلة هو x=2
إذن، طول ضلع قاعدة المنحوتة هو 2m، وارتفاعها 3m
ليكن ، حيث a,b ثوابت و
21) إذا كان (x - 3) عاملا من عوامل الاقتران f(x)؛ فأبين أن 3a+b=4
22) إذا كان باقي قسمة f(x) على x - 2 يساوي 15- ؛ فأبين أن 2a+b=3
23) أجد قيمة كل من a، وb.
بطرح المعادلة الناتجة في السؤال 22 من المعادلة الناتجة في سؤال 21 نجد أن a=1، وبتعويض قيمة a في إحدى المعادلتين نجد أن b=1.
24) أحل المسألة الواردة في بداية الدرس.
الحلان السالبان مرفوضان لأن x أحد أبعاد الصندوق ولا يمكن أن يكون سالبا.
إذن، قيمة x التي تجعل حجم الصندوق هي 3m
مهارات التفكير العليا
25) مسألة مفتوحة: أكتب اقترانا من الدرجة الثالثة يكون (x - 3) أحد عوامله، ويكون باقي قسمته على (x+1) يساوي 8-.
26) أكتشف الخطأ: أوجدت سهام الأصفار النسبية المحتملة للاقتران ، وكان حلها كالآتي:
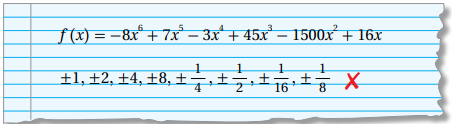
أبين الخطأ الذي وقعت فيه وأصححه.
قسمت سهام عوامل الحد الرئيس على عوامل الحد الثابت بعد إخراج العامل المشترك في حدود الاقتران وهو x.
الحل الصحيح هو:
27) تحد: أجد ناتج قسمة على باستعمال طريقة الجدول.
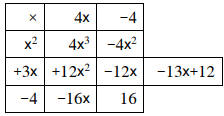
الناتج هو: 4x-4
الباقي: 13x+12-
28) تحد: أحلل المقدار
حل أسئلة كتاب التمارين
أستعمل طريقة الجدول؛ لأجد ناتج القسمة والباقي في كل مما يأتي:
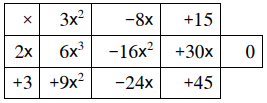
الناتج هو ، والباقي 0
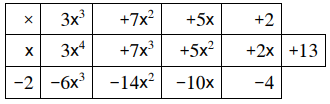
الناتج هو ، والباقي 13
3) يمثل الاقتران حجم متوازي المستطيلات المجاور، أجد الأبعاد الأخرى لمتوازي المستطيلات بدلالة x.
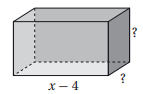
4) إذا كان باقي قسمة على x+2 يساوي (4-)؛ فما قيمة a؟
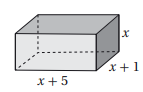
5) أجد أبعاد متوازي المستطيلات في الشكل المجاور إذا كان حجمه
6) إذا كان باقي قسمة على h(x)=x-1 يساوي 4، وكان (x+1) عاملا من عوامل f(x)؛ فما قيمة كل من a و b؟
أحلل كل اقتران مما يأتي تحليلا تاما:
أحل كلا من المعادلات الآتية:
11) أستعمل التمثيل البياني المجاور، الذي يمثل منحنى الاقتران ، لإيجاد أحد أصفاره النسبية، ثم أجد أصفاره جميعها.
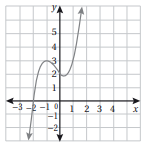
ليس له إلا صفر حقيقي واحد هو x - - 2.
12) يزيد ارتفاع مخروط 5cm على طول نصف قطر قاعدته. إذا كان حجم هذا المخروط ؛ فما أبعاده؟
طول نصف قطر قاعدته 6cm، وارتفاعه 11cm.